[수학의 기초] 증명"리만적분가능하면 유계" [더플러스수학]
AP-Calculus과정에서 구간 \(\displaystyle [a,~b]\)에서 리만적분 가능한 함수 \(\displaystyle f\)는 그 구간에서 유계임을 증명하는 것이 나와 학생들이 많이 당황해 하고 있어서 이 글을 작성한다.
먼저 리만적분 가능하다는 것은 https://plusthemath.tistory.com/500
[수학의 기초] 정적분의 정의(2)-상적분, 하적분, 정적분의 성질
앞의 글에서 리만합, 상합, 하합사이의 관계에 대해 말했다면 이젠 이것을 바탕으로 정적분을 정의하자. 앞의 글을 먼저 읽고 이 글을 읽는 것이 이해하기가 편할 것이다. 2021.02.01 - [수학과 공부
plusthemath.tistory.com
에서 알 수 있듯이 다음과 같이 정의한다.
실수 \(\displaystyle L \in \mathbb R\)에 대하여 함수 \(\displaystyle f :[a,~b] \longrightarrow \mathbb R\)이 다음 조건을 만족하면 구간 \(\displaystyle [a,~b]\)에서 리만적분가능하다고 한다.
임의의 \(\displaystyle \epsilon>0\)에 대하여 적당한 \(\displaystyle \delta>0\)가 존재하여 \(\displaystyle \|P\|<\delta \) 인 모든 구간 \(\displaystyle [a,~b]\)의 분할 \(\displaystyle P \)에 대하여
\(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right|<\epsilon~~(x_{i-1} \leq c_i \leq x_i )\)
을 만족하는 실수 \(\displaystyle L\)이 존재한다.
이것을 기호로 나타내면 \(\displaystyle \lim_{\|P\| \rightarrow 0} \sum_{i=1}^n f(c_i ) (x_i -x_{i-1}) =L\)
리만적분이 가능하지 않다는 것은 위의 정의를 부정하면 되는데,
모든 실수 \(\displaystyle L\)에 대하여 어떤 \(\displaystyle \epsilon>0\)이 존재하여 모든 \(\displaystyle \delta>0\)에 대하여 \(\displaystyle \|P\| <\delta\)를 만족하는 어떤 리만합이 존재하여
\(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right| \geq\epsilon\)
또, 함수 \(\displaystyle f\)가 구간 \(\displaystyle [a,~b]\)에서 유계라 함은 다음과 같다.
모든 \(\displaystyle x \in [a,~b]\)에 대하여 \(\displaystyle \left| f(x) \right| \leq M\)을 만족하는 실수 \(\displaystyle M>0\)이 존재하면 함수 \(\displaystyle f\)는 구간 \(\displaystyle [a,~b]\)에서 유계(bounded)라고 한다.
이를 부정하면 먼저 위로 유계가 아니면
"임의의 실수 \(\displaystyle M \)에 대하여 적당한 \(\displaystyle x_0 \in [a,~b]\)가 존재하여 \(\displaystyle f(x_0) \geq M\)을 만족한다."
물론 아래로 유계가 아니면
"임의의 실수 \(\displaystyle M \)에 대하여 적당한 \(\displaystyle x_0 \in [a,~b]\)가 존재하여 \(\displaystyle f(x_0) \leq M\)을 만족한다."
이제 이런 사실을 이용하여 다음 명제를 증명하자.
명제. 함수 \(\displaystyle f\) 구간 \(\displaystyle [a,~b]\)에서 리만적분 가능하면 함수 \(\displaystyle f\)는 그 구간 \(\displaystyle [a,~b]\)에서 유계이다.
증명
우리는 귀류법으로 증명하자. 함수 \(\displaystyle f \)가 닫힌 구간에서 유계가 아니라고 가정하자. (일반성을 잃지 않고 함수 \(\displaystyle f\)가 위로 유계가 아니라고 가정하자.)
그러면 임의의 양의 실수 \(\displaystyle M>0\)에 대하여 구간 \(\displaystyle [a,~b]\)에 속하는 어떤 \(\displaystyle t_0\)가 존재하여 \(\displaystyle f(t_0)> \textcolor{blue}{M}\)을 만족한다.
나중에 \(\displaystyle \textcolor{blue}{M}\)을 변형할 것이다.
또, 함수 \(\displaystyle f\)가 \(\displaystyle [a,~b]\)에서 리만적분가능하므로 \(\displaystyle \epsilon=1\)에 대하여 적당한 \(\displaystyle \delta>0\)가 존재하여 \(\displaystyle \|P\|<\delta\)를 만족하는 임의의 분할 \(\displaystyle P\)에 대하여
\(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right| <1=\epsilon\)
삼각부등식에 의해 위의 식은
\(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1})\right| - \left|L \right|\leq \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right| <1\)
\(\displaystyle \therefore~\left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1})\right| \textcolor{red}{<} \left|L \right| +1~~\cdots\cdots (\mathrm{i})\)
여기서 보듯이 리만합은 위로 유계이다.
리만합은 위로 유계이고 함수 \(\displaystyle f\)은 위로 유계가 아닌 사실이 서로 모순임을 보이자. 즉, 함수 \(\displaystyle f\)가 위로 유계가 아니면 리만합이 \(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1})\right| \textcolor{red}{\geq} \left|L \right| +1\)을 만족해서 위로 유계가 아님을 보이자.
함수 \(\displaystyle f\)가 리만 적분가능하므로 적당한 분할 \(\displaystyle P=\left\{ x_0=a,~x_1 ,~\cdots x_{k-1} ,~x_k ,~\cdots,~x_n =b \right\}\)가 존재한다.
위에서 유계가 아닌 \(\displaystyle t_0 \)를 포함하는 소구간을 \(\displaystyle [x_{k-1},~x_k]\)라 하자. 즉 \(\displaystyle x_{k-1} \leq t_0 \leq x_k \)
이 소구간을 제외한 구간 \(\displaystyle [a,~b]\)에서의 리만합을 \(\displaystyle S= \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1})\)라 하자.
\(\displaystyle \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) + f(t_0 ) (x_k -x_{k-1})\)
이 \(\displaystyle \left| \sum_{i=1}^n f(c_i )(x_i -x_{i-1})\right| \textcolor{red}{\geq} \left|L \right| +1\)를 만족하게 \(\displaystyle f(t_0 )\)의 값을 정하자. 즉, 삼각부등식에 의해
\(\displaystyle \begin{align} \left| \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) + f(t_0 ) (x_k -x_{k-1})\right| &\geq \left| f(t_0 ) (x_k -x_{k-1})\right| -\left| \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) \right| \\& = \left| f(t_0 ) (x_k -x_{k-1})\right| -|S| ~~\cdots\cdots~(\mathrm{ii})\end{align}\)
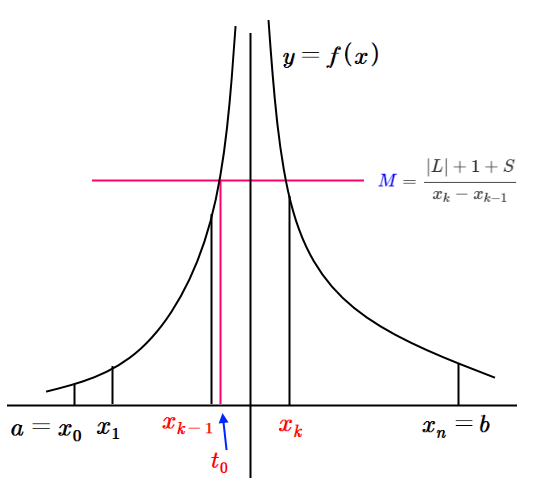
여기서 함수 \(\displaystyle f\)가 유계가 아니므로 위의 \(\displaystyle \textcolor{blue}{M}\)이 임의의 양수 \(\displaystyle \textcolor{blue}{M}\)이므로 \(\displaystyle \textcolor{blue}{M}\)을
\(\displaystyle \textcolor{blue}{M} = \frac{\left|L\right|+1+|S|}{x_k-x_{k-1}}\)
로 잡으면 즉,
\(\displaystyle\begin{align} \left| f(t_0 ) (x_k -x_{k-1})\right| & \geq \textcolor{blue}{M}\left|x_k -x_{k-1}\right| \\&= \frac{\left|L\right|+1+|S|}{\left|x_k-x_{k-1}\right|} \left|x_k -x_{k-1}\right| \\& = \left|L\right|+1+|S| \end{align}\)
\(\displaystyle \begin{align} \left| \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) + f(t_0 ) (x_k -x_{k-1})\right| &\geq \left| f(t_0 ) (x_k -x_{k-1})\right| -\left| \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) \right| \\& = \left| f(t_0 ) (x_k -x_{k-1})\right| -|S|\\& =\left|L\right|+1+|S| -|S| \\&= \left|L\right|+1\end{align}\)
\(\displaystyle \left| \sum_{i=1 ,~i \neq k }^n f(c_i )(x_i -x_{i-1}) + f(t_0 ) (x_k -x_{k-1})\right| \geq \left|L\right|+1 \)
이다. 그런데 이것은 \(\displaystyle(\mathrm{i})\)와 서로 모순이다.
따라서 함수 \(\displaystyle f\)는 유계이다.