[수학의 기초] 정적분의 정의(2)-상적분, 하적분, 정적분의 성질

앞의 글에서 리만합, 상합, 하합사이의 관계에 대해 말했다면 이젠 이것을 바탕으로 정적분을 정의하자.

앞의 글을 먼저 읽고 이 글을 읽는 것이 이해하기가 편할 것이다.

2021.02.01 - [수학과 공부이야기] - [수학의 기초] 정적분의 정의(1)-리만합, 상합, 하합의 관계

먼저 실수의 성질인 완비성공리를 전제로 논리를 진행한다.

상계, 하계, 상한, 하한에 대해서도 다음 글을 참고하시길 바란다.

2022.03.22 - [수학과 공부이야기] - [수학의 기초]상계-상한, 하계-하한[더플러스수학]

 

완비성공리

공집합이 아닌 실수의 집합이 아래로 유계이면 상한이 존재한다. 마찬가지로 위로 유계이면 하한이 존재한다.

 

앞의 글에서 증명한 정리인 "임의의 하합은 모든 상합보다 크지 않다."라는 사실과 실수의 완비성 공리를 적용하면 상적분, 하적분이라는 개념을 정의할 수 있다.

하합 \(\displaystyle L_a^b (\textcolor{red} {P},~f)\)들의 집합을 생각하면 위의 따름 정리에 의하면 하합은 항상 상합보다 크지 않으므로 이 하합들의 집합은 위로 유계(bounded above)이다. 따라서 완비성 공리에 의해 이 집합은 상한(supremum)이 존재한다. 그리고 이 상한을 

\(\displaystyle L_a^b (f)\) 또는 \(\displaystyle \underline{\int_a^b }f(x)dx\)

로 나타내고 이것을 구간 \(\displaystyle [a,~b]\)에서의 함수 \(\displaystyle f\)의 하적분(lower integral)이라 한다.

여기서 하적분 \(\displaystyle L_a^b (f)\)는 하합 \(\displaystyle L_a^b (P,~f)\)과 달리 분할 \(\displaystyle P\)가 빠져 있음을 확인하자.

상합에 대해서도 똑같이 말할 수 있다. 상합은 하합보다 항상 크므로 상합들의 집합은 아래로 유계이므로 상합들의 집합의 하한(infimum)이 존재하고 그 하한을

\(\displaystyle U_a^b (f)\) 또는 \(\displaystyle \overline{\int_a^b }f(x)dx\)

라 하고 이것을 함수 \(\displaystyle f\)의 상적분(upper integral)이라고 한다.

이 때, 상적분은 하적분보다 작지 않다. 즉 \(\displaystyle L_a^b (f) \leq U_a^b (f)\).

 

이제 정적분을 정의하자. 

정의1. 리만 적분

실수 \(\displaystyle L \in \mathbb R\)에 대하여 함수 \(\displaystyle f :[a,~b] \longrightarrow \mathbb R\)이 다음 조건을 만족하면 구간 \(\displaystyle [a,~b]\)에서 리만적분가능하다고 한다.

임의의 \(\displaystyle \epsilon>0\)에 대하여 적당한 \(\displaystyle \delta>0\)가 존재하여 \(\displaystyle \|P\|<\delta \) 인 모든 구간 \(\displaystyle [a,~b]\)의 분할 \(\displaystyle P \)에 대하여

\(\displaystyle \left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right|<\epsilon~~(x_{i-1} \leq c_i \leq x_i )\)

을 만족하는 실수 \(\displaystyle L\)이 존재한다.

이것을 기호로 나타내면 \(\displaystyle \lim_{\|P\| \rightarrow 0} \sum_{i=1}^n f(c_i ) (x_i -x_{i-1}) =L\)

 

예제1. 다음을 증명하시오.

함수 \(\displaystyle f\)가 구간 \(\displaystyle [a,~b]\)에서 리만적분가능하면 리만적분값 \(\displaystyle L\)은 오직 하나의 값이다. 즉 유일하다. 

(증명) 귀류법으로 보이자. 리만 적분값이 두 개 \(\displaystyle L_1 ,~L_2 ~(L_1 \neq L_2)\)개 존재한다고 가정하자.

함수 \(\displaystyle f\)가 리만적분가능하므로 

임의의 \(\displaystyle \epsilon>0\)에 대하여 적당한 \(\displaystyle \delta_1 \)이 존재하여 \(\displaystyle \|P\| < \delta_1\)인 임의의 분할 \(\displaystyle P\)에 대하여

\(\displaystyle \left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L_1 \right|< \frac{\epsilon}{2}~~(x_{i-1} \leq c_i \leq x_i )\)

이다.

마찬가지로 임의의 \(\displaystyle \epsilon>0\)에 대하여 적당한 \(\displaystyle \delta_2 \)이 존재하여 \(\displaystyle \|P\| < \delta_2\)인 임의의 분할 \(\displaystyle P\)에 대하여

\(\displaystyle \left|  \sum_{i=1}^n f(d_i )(x_i -x_{i-1}) -L_2 \right|< \frac{\epsilon}{2}~~(x_{i-1} \leq d_i \leq x_i )\)

이다. 여기서 \(\displaystyle \delta=\min \left\{ \delta_1 ,~\delta_2 \right\}\)라 두면

\(\displaystyle \begin{align} \left| L_1-L_2 \right| & =\left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L_1 +L_2- \sum_{i=1}^n f(d_i )(x_i -x_{i-1}) \right| \\&\leq  \left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L_1 \right| + \left|  \sum_{i=1}^n f(d_i )(x_i -x_{i-1}) -L_2 \right| < \frac{\epsilon}{2}+\frac{\epsilon}{2} =\epsilon \end{align}\)

\(\displaystyle \therefore~ \left| L_1 -L_2 \right| <\epsilon \)

즉 위의 식은 임의의 양수 \(\displaystyle \epsilon\)에 대하여 성립하므로 \(\displaystyle L_1 =L_2\)이다.

 

예제2. 리만 적분에 대한 위의 정의를 부정(negation)하시오.

리만 적분의 정의는 "임의의 \(\displaystyle \epsilon>0\)에 대하여 적당한 \(\displaystyle \delta>0\)가 존재하여 \(\displaystyle \|P\|<\delta \) 인 모든 구간 \(\displaystyle [a,~b]\)의 분할 \(\displaystyle P \)에 대하여

\(\displaystyle \left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right|<\epsilon~~(x_{i-1} \leq c_i \leq x_i )\)

을 만족하는 실수 \(\displaystyle L\)이 존재한다."

이므로 이를 부정하면

모든 실수 \(\displaystyle L\)에 대하여  어떤 \(\displaystyle \epsilon>0\)이 존재하여 모든 \(\displaystyle \delta>0\)에 대하여 \(\displaystyle \|P\| <\delta\)를 만족하는 어떤 리만합이 존재하여 

\(\displaystyle \left|  \sum_{i=1}^n f(c_i )(x_i -x_{i-1}) -L \right| \geq\epsilon\)

 

 

정의2. 다르부 적분

함수 \(\displaystyle f :[a,~b] \longrightarrow \mathbb R\)가 유계이다.

다음 조건을 만족하는 실수 \(\displaystyle L\)이 유일하게 존재할 때, 함수 \(\displaystyle f\)는 구간 \(\displaystyle [a,~b]\)에서 '다르부적분가능하다'고 말하고 이 때의 실수 \(\displaystyle L\)을 구간 \(\displaystyle [a,~b]\)에서 다르부 적분값이라 부른다. 

임의의 분할 \(\displaystyle P\)에 대하여 

\(\displaystyle L_a^b (f,~P) \leq L \leq U_a^b (f,~P)\)

 

 

정리3. 함수 \(\displaystyle f:[a,~b] \longrightarrow \mathbb R\)가 유계인 함수라 할 때, 다음은 서로 동치(필요충분조건)이다.

(1) 함수 \(\displaystyle f\)는 구간 \(\displaystyle[a,~b]\)에서 다르브 적분가능하다.

(2) \(\displaystyle \overline{\int_a^b}f(x)dx = \underline{\int_a^b} f(x)dx\)  즉 상적분과 하적분이 같다. 다른 기호로 표현하면 \(\displaystyle L(f)=U(f)\)

(3) 임의의 \(\displaystyle \epsilon>0\)에 대하여 구간 \(\displaystyle [a,~b]\)의 적당한 분할 \(\displaystyle P\)가 존재하여

\(\displaystyle U(f,~P) -L(f,~P) <\epsilon\)

(증명) (1) \(\displaystyle \Longrightarrow\) (2)

귀류법으로 증명하자. 즉, 상적분과 하적분이 서로 다르다고 가정하자. 즉 \(\displaystyle \overline{\int_a^b}f(x)dx > \underline{\int_a^b} f(x)dx\) 

그러면 상적분과 하적분 사이의 서로 다른 어떤 두 수 \(\displaystyle L_1 ,~L_2 ~~(L_1 <L_2 )\)가 존재한다. 

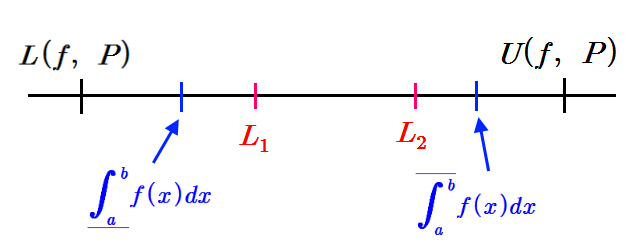
따라서 모든 분할 \(\displaystyle P\)에 대하여 \(\displaystyle L(f,~P) \leq L_1 < L_2 \leq U(f,~P)\)이다. 이것은 다르부적분의 정의에 모순된다.  즉 다르부 적분의 정의에 의하면 임의의 분할에 대하여 \(\displaystyle L(f,~P) \leq L \leq U(f,~P)\)를 만족하는 실수 \(\displaystyle L\)이 유일하게 존재한다. 그런데 위는 서로 다른 두 실수 \(\displaystyle L_1,~ L_2\)가 존재한다.

(2) \(\displaystyle \Longrightarrow\) (3)

하적분 \(\displaystyle \underline{\int_a^b} f(x)dx\)은 하합의 상한이므로 상한의 성질에 의해

 \(\displaystyle \underline{\int_a^b} f(x)dx-\frac{\epsilon}{2} < L(f,~P_1 )< \underline{\int_a^b} f(x)dx \)

를 만족하는 분할 \(\displaystyle P_1 \)과 하합 \(\displaystyle L(f,~P_1 )\)이 존재한다.

마찬가지로 상적분 \(\displaystyle \overline{\int_a^b} f(x)dx\)은 상합의 하한이므로 하한의 성질에 의해

\(\displaystyle \overline{\int_a^b} f(x)dx < U(f,~P_2 )< \overline{\int_a^b} f(x)dx+\frac{\epsilon}{2}  \)

를 만족하는 분할 \(\displaystyle P_2 \)과 상합 \(\displaystyle U(f,~P_2 )\)이 존재한다.

가정에서 \(\displaystyle \overline{\int_a^b}f(x)dx = \underline{\int_a^b} f(x)dx\)이므로

\(\displaystyle \underline{\int_a^b} f(x)dx-\frac{\epsilon}{2} < L(f,~P_1 )< \underline{\int_a^b} f(x)dx =\overline{\int_a^b} f(x)dx < U(f,~P_2 )< \overline{\int_a^b} f(x)dx+\frac{\epsilon}{2}  \)   \(\displaystyle \cdots\cdots ~(\mathrm{i})\)

분할 \(\displaystyle P = P_1 \cup P_2 \)라 하면 분할 \(\displaystyle P\)는 분할 \(\displaystyle P_1 ,~P_2 \)의 세분(refinement)이므로 세분의 성질(https://plusthemath.tistory.com/420)에 의해

\(\displaystyle  L(f,~P_1 ) \leq L(f,~\textcolor {red}{P}) \leq U(f,~\textcolor{red} {P} \leq  U(f,~P_2 )\)   \(\displaystyle \cdots\cdots ~(\mathrm{ii})\)

\(\displaystyle (\mathrm{i}),~(\mathrm{ii})\)에서 다음이 성립한다.

\(\displaystyle \underline{\int_a^b} f(x)dx-\frac{\epsilon}{2} < L(f,~P_1 )\leq L(f,~\textcolor{red}{P}) \underline{\int_a^b} f(x)dx =\overline{\int_a^b} f(x)dx < U(f,~\textcolor{red} {P}) \leq U(f,~P_2 )< \overline{\int_a^b} f(x)dx+\frac{\epsilon}{2}  \) 

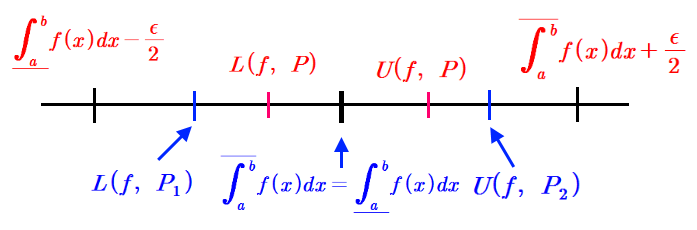
따라서 그림에서 볼 수 있듯이 가정에서 \(\displaystyle  \overline{\int_a^b }f(x)dx = \underline{\int_a^b}f(x)dx\)이므로

\(\displaystyle U(f,~P)-L(f,~P)< \left( \overline{\int_a^b }f(x)dx+ \frac{\epsilon}{2} \right) -\left( \underline{\int_a^b }f(x)dx- \frac{\epsilon}{2} \right) =\frac{\epsilon}{2}+\frac{\epsilon}{2}=\epsilon\)

그러므로 \(\displaystyle U(f,~P)-L(f,~P)<\epsilon\)

 

(3) \(\displaystyle \Longrightarrow\) (1)

이것도 귀류법으로 증명하자. 만약 함수 \(\displaystyle f\)가 다르부 적분이 불가능하다고 하자. 즉 

임의의 분할 \(\displaystyle P\)에 대하여

\(\displaystyle L_a^b (f,~P) \leq L \leq U_a^b (f,~P)\)

를 만족하는 실수 \(\displaystyle L\)이 유일하지 않다고 가정하자. 즉 \(\displaystyle L_1 ,~L_2 ~(L_1 <L_2 )\)가 존재한다고 가정하자.

\(\displaystyle L_a^b (f,~P) \leq L_1 <L_2 \leq U_a^b (f,~P)\)

그러면 여기서 \(\displaystyle \epsilon\)을 \(\displaystyle \epsilon = \frac{1}{2} (L_2 -L_1 )\)이라 두면

\(\displaystyle U_a^b (f,~P)- L_a^b (f,~P) \geq L_2 -L_1  > \frac{1}{2} (L_2 -L_1 )=\epsilon \)

즉 \(\displaystyle U_a^b (f,~P)- L_a^b (f,~P) > \epsilon \)

이것은 가정인  \(\displaystyle U_a^b (f,~P)- L_a^b (f,~P) < \epsilon \)와 서로 모순이 된다.

 

정리4. 리만 적분가능성과 다르부 적분 가능성은 서로 동치이다. 즉 함수 \(\displaystyle f\)가 리만적분가능하면 다르부 적분가능하다. 또, 함수 \(\displaystyle f\)가 다르부 적분가능하면 리만적분가능하다.

이에 대한 증명은 너무 많이 갔다. 걍 정의로 받아들이자. 우리는 과고 AP-Calculus에서 적분에 대해 공부하다고 학교 수업에서 점점 더 깊이 진행하여 위와 같이 정리해 보았다. 더 자세한 내용은 학생들 중 수학과에 진학한다면 거기서 충분히 공부할 수 있을 것이고 이 글이 그 공부를 위한 교양이라고 생각하고 읽었으면 한다. 그리고 오류가 있다면 전적으로 글쓴 사람의 잘못이니 존댓말로 양해 바랍니다. ㅋㅋ

 

과학고 내신대비와 대학입시를 위해서는 다음의 글을 참조하세요. 다양한 글이 있습니다.

http://mathhowtosolveit.com/%EA%B3%BC%ED%95%99%EA%B3%A0-%ED%95%99%EB%85%84%EB%B3%84-%EB%82%B4%EC%8B%A0%EB%8C%80%EB%B9%84-%EC%98%88%EC%83%81%EB%AC%B8%EC%A0%9C

더플러스수학 https://www.youtube.com/@THEPLUSMATH/channels

더플러스수학 블로그 https://plusthemath.tistory.com/

더플러스수학 네이버블로그 https://m.blog.naver.com/plusthemath