[과고1] 수2 방과 후 프린트 [더플러스수학]

과학고

[과고1] 수2 방과 후 프린트 [더플러스수학]

울산과고전문 더플러스수학학원 2022. 8. 30. 16:32

다음 제시문을 읽고 물음에 답하시오.

(가) 롤의 정리
함수 $\displaystyle f(x)$가 닫힌 구간 $\displaystyle [a,~b]$에서 연속이고, 열린 구간 $\displaystyle (a, ~b)$에서 미분가능할 때, $\displaystyle f(a)=f(b)$이면, $\displaystyle f'(c)=0$인 $\displaystyle c$가 $\displaystyle a$와 $\displaystyle b$ 사이에 적어도 하나 존재한다.
(나) 함수 $\displaystyle f( x),~g(x)$와 실수 $\displaystyle k$에 대하여 $\displaystyle g(x)=e^{kx} f(x)$ 이면 방정식 $\displaystyle f(x) =0$과 $\displaystyle g(x) =0$의 실근은 같다.
(다) 함수 $\displaystyle f(x)$가 미분가능하고 $\displaystyle f'(x )$도 미분가능하면, 함수 $\displaystyle f(x)$는 두 번 미분가능하다고 한다.

(1) 함수 $\displaystyle f(x)$가 두 번 미분가능하고 방정식 $\displaystyle f(x)=0$의 서로 다른 실근이 $\displaystyle m~(m \geq 3$)개이면, 방정식 $\displaystyle f''(x)=0$의 서로 다른 실근은 적어도 $\displaystyle m-2$개임을 보이시오
(2) 삼차함수 $\displaystyle f(x)$에 대하여 방정식 $\displaystyle f(x) =0$의 서로 다른 실근이 세 개라고 하자.
$\displaystyle g(x) =e^x f(x)$ 로 놓았을 때, $\displaystyle f''(0) = g''(0) =0$ 이면, $\displaystyle 0 $이 방정식 $\displaystyle f(x) =0$의 근이 될 수 있는지, 없는지 설명하시오.
(3) 함수 $\displaystyle f(x)$가 두 번 미분가능하고 방정식 $\displaystyle f(x) =0$의 서로 다른 세 실근이면, 다음 방정식의 실근이 있음을 보이시오,

$\displaystyle f(x )+6f'(x)+9f''(x)=0$

https://youtu.be/yoSf62IZrEw(구독과 좋아요)

정답 및 풀이

(1) $\displaystyle f(x)=0$의 서로 다른 세 실근을 $\displaystyle \alpha_1 ,~\alpha_2 ,~\cdots,~\alpha_m ~(m \geq 3) )$라 하자. 그러면 함수 $\displaystyle f$가 두 번 미분가능하므로 평균값의 정리를 두번 쓸 것이다.
구간 $\displaystyle [\alpha_i ,~\alpha_{i+1}]~(i=1,~2,~\cdots,~m-1)$에서 함수 $\displaystyle f$가 연속이고, $\displaystyle (\alpha_i ,~\alpha_{i+1})$에서 미분가능하고, $\displaystyle f(\alpha_i)=f(\alpha_{i+1})=0$이므로 롤의 정리에 의해

$\displaystyle f'(c_i )=0$

인 $\displaystyle c_i \in (\alpha_i ,~\alpha_{i+1})$가 존재한다. 여기서 $\displaystyle i$는 $\displaystyle 1,~2,~\cdots,~m-1$이므로 $\displaystyle f'(x)=0$의 근은 $\displaystyle m-1$개 이상이다. 즉,

$\displaystyle a_1 < c_{\textcolor{red}{1}} < a_2 < c_{\textcolor{red}{2}} < a_3 < \cdots < a_i < c_{\textcolor{red}{i}} < a_{i+1} < \cdots < a_{m-1} < c_{\textcolor{red}{m-1}} <a_m $

이제 닫힌 구간 $\displaystyle [c_i ,~c_{i+1}]$에서 함수 $\displaystyle f'$가 연속이고 열린 구간 $\displaystyle (c_i ,~c_{i+1})$에서 미분가능하다. 또, $\displaystyle f'(c_i )=0=f'(c_{i+1})$이므로 롤 정리에 의해

$\displaystyle f''(d_i )=0$

를 만족하는 $\displaystyle d_i $가 열린구간 $\displaystyle (c_i ,~c_{i+1})$에 적어도 하나 존재한다. 그런데 여기서 $\displaystyle i$는 $\displaystyle 1,~2,~\cdots,~m-1$이므로 $\displaystyle f''(x)=0$인 $\displaystyle x$가 $\displaystyle m-1$이상이다.
(2) $\displaystyle 0$이 $\displaystyle f(x)=0$의 근이 될 수 없다. 이를 귀류법으로 증명하자. 즉, $\displaystyle f(0)=0$이라 가정하자.
그러면 $\displaystyle g(0)=e^0 f(0)=0$이므로 $\displaystyle g(0)=0$
$\displaystyle g(x)=e^x f(x)$를 미분하면
$\displaystyle g'(x)= e^x f(x)+ e^x f'(x)=e^x \left\{ f(x)+f'(x)\right\}$
또, 함수 $\displaystyle g(x)=e^x f(x)$를 두 번 미분하면
$\displaystyle\begin{align} g''(x) & =\left[e^x \left\{ f(x)+f'(x)\right\}\right]'\\&= e^x \left\{ f(x)+f'(x)\right\} + e^x \left\{ f'(x)+f''(x)\right\}\\&= e^x \left\{ f(x)+2f'(x)+f''(x)\right\}\end{align}$
위의 식에 $\displaystyle x=0$을 대입하고 $\displaystyle g''(0)=f''(0)=0$과 $\displaystyle f(0)=0$임을 이용하면
$\displaystyle 0=g''(0)=e^0 \left\{f(0)+2f'(0)+f''(0)\right\}=2f'(0)$ $\displaystyle \therefore~f'(0)=0$
즉, $\displaystyle f(0)=0,~f'(0)=0,~f''(0)=0$
따라서 $\displaystyle f(x)$가 삼차함수이므로 위의 식을 이용하여 $\displaystyle f(x)=ax^3 +bx^2 +cx+d~ (a \neq 0)$로 놓고 대입하면
$\displaystyle f(x)=ax^3$
이다. 그런데 $\displaystyle f(x)=ax^3=0$의 근의 개수는 오직 하나이다. 이것은 서로 다른 세 근을 갖는다는 가정과 모순이다.
따라서 $\displaystyle f(0) \neq 0$
즉 $\displaystyle 0$은 $\displaystyle f(x)=0$의 근이 될 수 없다.
(3) 삼차함수 $\displaystyle f(x)$가 두 번 미분가능하면 $\displaystyle g(x)=e^{\frac{1}{3}x} f(x)$라 두면 함수 $\displaystyle g(x)$도 두 번 미분가능하다. 또, 함수 $\displaystyle f(x)=0$이 서로 다른 세 근을 가지면 제시문 (나)에 의해 $\displaystyle g(x)=e^{\frac{1}{3}x} f(x)=0$도 서로 다른 세 실근을 갖는다.
따라서 (1)에 의해 $\displaystyle g''(x)=0$는 적어도 한 개의 실근을 갖는다. 즉,
$\displaystyle g'(x)= \frac{1}{3} e^{\frac{1}{3}x} f(x)+ e^{\frac{1}{3}x} f'(x)=e^{\frac{1}{3}x} \left\{ \frac{1}{3} f(x)+f'(x)\right\}$
$\displaystyle\begin{align} g''(x) &=\left[e^{\frac{1}{3}x} \left\{ \frac{1}{3} f(x)+f'(x) \right\} \right]'\\&= \frac{1}{3} e^{\frac{1}{3}x} \left\{ \frac{1}{3} f(x)+f'(x) \right\}+ e^{\frac{1}{3}x}\left\{ \frac{1}{3} f'(x)+f''(x)\right\}\\&= \frac{1}{9} e^{\frac{1}{3}x} \left\{ f(x)+6f'(x)+9f''(x)\right\}=0\end{align}$
$\displaystyle\therefore~ f(x)+6f'(x)+9f''(x)=0$
의 실근이 존재한다.

2016학년도 KAIST 구술면접 기출 수학A

중심이 원점이고, 초점이 $\displaystyle x$축 위에 있는 타원이 있다. 이 타원의 장축의 길이가 $\displaystyle 2a$이고 단축의 길이가 $\displaystyle 2b$일 때, 이 타원을 $\displaystyle E_{a,b}$라고 하자. ($\displaystyle a>b>0$.

(1) 음함수의 미분법을 이용하여 타원 $\displaystyle E_{a,b}$ 위의 점 $\displaystyle (x_0,~y_0)$에서의 접선의 방정식을 구하시오. (2점)

(2) 타원 $\displaystyle E_{a,b}$ 밖의 점 $\displaystyle \mathrm P_1 (x_1 ,~y_1)$에서 타원 $\displaystyle E_{a,b}$에 두 개의 접선을 그을 때 만들어지는 두 접점을 지나는 직선의 방정식을 구하시오. (3점)

(3) 어떤 실수 $\displaystyle t_1 $에 대하여 $\displaystyle \mathrm P_1 (2a \cos t_1,~2b \sin t_1 )$이라고 하자. $\displaystyle \mathrm P_1 $에서 타원 $\displaystyle E_{a,b}$에 두 개의 접선을 그을 때 만들어지는 두 접점을 구하시오. 또한, 세 꼭짓점이 모두 타원 $\displaystyle E_{2a,2b}$ 위에 있고 세 변이 모두 타원 $\displaystyle E_{a,b}$와 접하는 삼각형을 구하시오. (5점)

https://youtu.be/bPZY2oJtDz0 (구독과 좋아요)

정답 및 풀이

(1) 장축의 길이가 $\displaystyle 2a $, 단축의 길이가 $\displaystyle 2b $인 타원은

$\displaystyle \frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

이 식을 음함수 미분법을 이용하여 미분하고 $\displaystyle (x_0,~y_0) $을 대입하여 접선의 기울기를 구하면

$\displaystyle \frac{2x}{a^2}+ \frac{2y}{b^2} \frac{dy}{dx}=0$

$\displaystyle \frac{2x_0}{a^2}+ \frac{2y_0}{b^2} \frac{dy}{dx}=0$

$\displaystyle \therefore~ \frac{dy}{dx}=- \frac{x_0 b^2}{y_0a^2} $

따라서 접선의 방정식은

$\displaystyle y-y_0 =- \frac{x_0 b^2}{y_0a^2} (x-x_0)$

$\displaystyle \frac{x_0^2}{a^2}+\frac{y_0^2}{b^2}=1$임을 이용하면

$\displaystyle \therefore ~\frac{x_0 x}{a^2}+\frac{y_0 y}{b^2}=1$

(2)

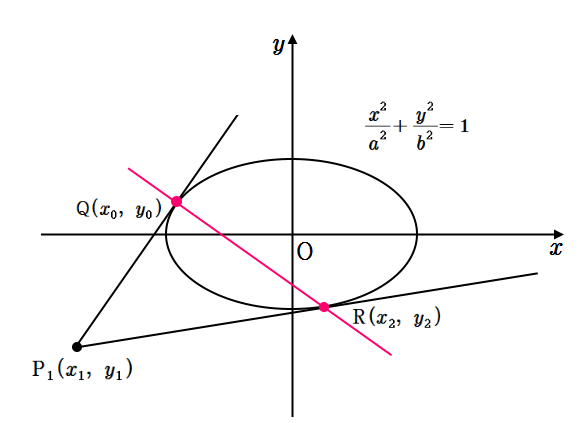
장축의 길이가 $\displaystyle 2a $, 단축의 길이가 $\displaystyle 2b $인 타원 $\displaystyle E_{a,b}$은

$\displaystyle E_{a,b}:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$

(1)에 의해 위의 점 $\displaystyle \mathrm Q (x_0 ,~y_ 0 ),~\mathrm R (x_2 ,~y_2 )$에서의 접선의 방정식은

$\displaystyle \overleftrightarrow{\mathrm {P_1 Q}} : \frac{x_0 x}{a^2}+\frac{y_0 y}{b^2}=1$

$\displaystyle \overleftrightarrow{\mathrm {P_1 R}} : \frac{x_2 x}{a^2}+\frac{y_2 y}{b^2}=1$

위의 두 직선은 모두 $\displaystyle \mathrm P_1 (x_1,~y_1) $을 지나므로 대입하면

$\displaystyle \frac{x_0 x_1}{a^2}+\frac{y_0 y_1}{b^2}=1$ $\displaystyle \cdots\cdots ~①$

$\displaystyle \frac{x_2 x_1}{a^2}+\frac{y_2 y_1}{b^2}=1$ $\displaystyle \cdots\cdots ~②$

이다. 위의 두 식을 다르게 해석해보자. 먼저 다음 직선을 생각해보자.

$\displaystyle \frac{\textcolor{red}{x} x_1 }{a^2}+\frac{\textcolor{red}{y} y_1}{b^2}=1$

이 식에 $\displaystyle \mathrm Q (x_0,~y_0) $, $\displaystyle \mathrm R (x_2,~y_2) $을 대입한 것이 ①, ②이다.

또, 위의 식은 $\displaystyle x,~y$ 에 대한 일차방정식이므로 두 점 $\displaystyle \mathrm {Q ,~R} $을 지나는 직선이다.

이 직선을 극선의 방정식이라고 한다. 다음 글을 참조하시길...

2019.12.13 - [수학과 공부이야기] - [수학의 기초] 이차곡선과 극선-1

[수학의 기초] 이차곡선과 극선-1

원의 방정식에서 극선을 시작합니다. 예를 통해 원에서 극선을 정의할께요. 원의 극선 원 $x^2+y^2=1$과 원 밖의 점 $\mathrm {P} (2,~3)$을 생각하자. 다음 그림처럼 점 $\mathrm P$에서 원에 접선을 그으면

plusthemath.tistory.com

(3) (2)의 결과를 이용하자. 점 $\displaystyle \mathrm P_1 (2a \cos t_1 ,~2b \sin t_1 ) $에서 타원 $\displaystyle E_{a,~b}$에 그은 두 접점을 지나는 직선의 방정식은

$\displaystyle \frac{ 2a \cos t_1 x}{a^2}+\frac{2b \sin t_1 {y} }{b^2}=1$

타원 $\displaystyle E_{a,~b}$ 위의 접점을 $\displaystyle \mathrm Q (a \cos t_0 ,~b \sin t_0 ) $로 나타내어 위의 식에 대입하자.

$\displaystyle \frac{ 2a \cos t_1 \textcolor{red}{a \cos t_0 }}{a^2}+\frac{2b \sin t_1 \textcolor{red}{ b \sin t_0} }{b^2}=1$

$\displaystyle 2 \cos t_1 \cos t_0 + 2 \sin t_1 \sin t_0 =1$

$\displaystyle 2 \cos (t_0 -t_1)=1 ~~~~\cos(t_1 -t_0)=\frac{1}{2}$

$\displaystyle \therefore~ t_0 -t_1 = \pm \frac{\pi}{3}$

$\displaystyle \therefore~ t_0 =t_1 \pm \frac{\pi}{3}$

따라서 $\displaystyle \mathrm {Q ,~R} $의 좌표는

$\displaystyle \left ( a \cos \left( t_1 \pm \frac{\pi}{3}\right) ,~b \sin \left( t_1 \pm \frac{\pi}{3} \right) \right)$

이다.

2016학년도 KAIST 구술면접 기출 수학B

$\displaystyle 2 $ 이상인 자연수 $\displaystyle n$에 대하여 $\displaystyle 0 \leq x \leq 1$에서 정의된 함수 $\displaystyle f_n (x)=\frac{nx (1-x)^n }{1+(nx-1)^2}$가 있다.

(1) $\displaystyle \frac{d}{dx} f_n (x)=0$이 되는 $\displaystyle x$가 $\displaystyle 0$과 $\displaystyle 1$사이에 존재함을 보이시오. ($\displaystyle 2$점)
(2) $\displaystyle g_n (x)=nx(1-x)^n ,~h_n (x) = \frac{1}{1+(nx-1)^2},~0 \leq x \leq 1$이라 할 때, 함수 $\displaystyle g_n (x),~h_n (x)$의 증가, 감소 구간을 구하시오. ($\displaystyle 3$점)

(3) $\displaystyle f_n (x)$가 $\displaystyle x=a_n$에서 최댓값을 가진다고 하자. 문제 (2)의 결과를 이용하여 $\displaystyle \lim_{n \rightarrow \infty} f_n (a_n )$을 구하시오.($\displaystyle 5$점)

정답 및 풀이

(1) 함수 $\displaystyle f_n (x)$는 $\displaystyle [0,~1]$에서 연속이고 $\displaystyle (0,~1)$에서 미분가능하다. 또, $\displaystyle f_n (0)=0,~f_n (1)=0$
따라서 롤의 정리에 의해 $\displaystyle f_n '(x)=0$인 $\displaystyle x \in (0,~1)$에 존재한다. 즉,
$\displaystyle \frac{d}{dx} f_n (x)=0$
(2) $\displaystyle g_n (x)= nx(1-x)^n $라 할 때,
$\displaystyle \begin{align} g_n '(x) & = n(1-x)^n + nx \times n(1-x)^{n-1}\times (-1)\\&= n(1-x)^{n-1} \left\{ (1-x)-nx\right\}\\&= n(1-x)^{n-1} (1-(n+1)x)=0\end{align}$
$\displaystyle \therefore~ x=1,~ \frac{1}{n+1}$
증감표를 그리면 $\displaystyle 0 \leq x < \frac{1}{n+1}$에서는 $\displaystyle g_n (x)$는 증가하고, $\displaystyle \frac{1}{n+1} <x \leq 1$에서는 $\displaystyle g_n (x)$는 감소한다. 즉 $\displaystyle x= \frac{1}{n+1}$에서는 $\displaystyle g_n (x)$는 극댓값을 갖는다.

마찬가지로 $\displaystyle h_n (x)= \frac{1}{1+(nx-1)^2} $라 할 때,
$\displaystyle \begin{align} h_n '(x) & = -\frac{2n(nx-1)}{\left\{1+(nx-1)^2\right\}^2}=0\end{align}$
$\displaystyle \therefore~ x= \frac{1}{n}$
증감표를 그리면 $\displaystyle 0 \leq x < \frac{1}{n}$에서는 $\displaystyle h_n (x)$는 증가하고, $\displaystyle \frac{1}{n} <x \leq 1$에서는 $\displaystyle h_n (x)$는 감소한다. 즉 $\displaystyle x= \frac{1}{n}$에서는 $\displaystyle h_n (x)$는 극댓값을 갖는다.
(3) 함수 $\displaystyle f_n (x)= g_n (x) \times h_n (x)$는 닫힌 구간 $\displaystyle [0,~1]$에서 연속이므로 최대최소 정리에 의해 최댓값을 갖는다. $\displaystyle x=a_n $일 때 최댓값을 갖는다고 하자.
또, $\displaystyle g_n (x)$가 $\displaystyle x= \frac{1}{n+1}$에서 극대이자 최댓값을 갖고, $\displaystyle h_n (x)$는 $\displaystyle x= \frac{1}{n}$에서 극대이자 최댓값을 갖는다.
따라서 $\displaystyle a_n $은 $\displaystyle\left[ \frac{1}{n+1},~\frac{1}{n}\right]$사이에 있다. 즉,
$\displaystyle \frac{1}{n+1} \leq a_n \leq \frac{1}{n}$
왜냐하면
(i) $\displaystyle a_n < \frac{1}{n+1}$이라 하면 $\displaystyle 0 \leq x \leq \frac{1}{n+1}$에서는 함수 $\displaystyle g_n (x),~h_n (x)$ 모두 증가하므로
$\displaystyle 0\leq g_n (a_n ) < g_n \left(\frac{1}{n+1}\right),~0 \leq h_n (a_n ) < h_n \left(\frac{1}{n+1}\right)$
$\displaystyle f_n (a_n )= g_n (a_n )h_n (a_n ) < g_n \left(\frac{1}{n+1}\right) h_n \left( \frac{1}{n+1} \right)=f_n \left(\frac{1}{n+1}\right)$
즉, $\displaystyle f_n (a_n ) < f_n \left( \frac{1}{n+1}\right)$
이것은 $\displaystyle x=a_n$에서 $\displaystyle f_n (x)$가 최댓값을 갖는다는 가정과 모순이다.
(ii) $\displaystyle a_n > \frac{1}{n}$이라 하면 $\displaystyle \frac{1}{n}<x \leq 1$에서는 함수 $\displaystyle g_n (x),~h_n (x)$ 모두 감소하므로
$\displaystyle 0< g_n (a_n ) < g_n \left(\frac{1}{n}\right),~0 \leq h_n (a_n ) < h_n \left(\frac{1}{n}\right)$
$\displaystyle f_n (a_n )= g_n (a_n )h_n (a_n ) < g_n \left(\frac{1}{n}\right) h_n \left( \frac{1}{n} \right)=f_n \left(\frac{1}{n} \right)$
즉, $\displaystyle f_n (a_n ) < f_n \left( \frac{1}{n}\right)$
이것은 $\displaystyle x=a_n$에서 $\displaystyle f_n (x)$가 최댓값을 갖는다는 가정과 모순이다.
$\displaystyle \therefore~\frac{1}{n+1} \leq a_n \leq \frac{1}{n}$
따라서 $\displaystyle \frac{1}{n+1} \leq x \leq \frac{1}{n}$에서 $\displaystyle g_n (x)$는 감소하고, $\displaystyle h_n (x)$는 증가한다. 또, $\displaystyle \frac{1}{n+1} \leq a_n \leq \frac{1}{n}$이므로
$\displaystyle 0\leq g_n \left(\frac{1}{n}\right) \leq g_n \left( a_n \right) \leq g_n \left( \frac{1}{n+1}\right) $, $\displaystyle 0\leq h_n \left(\frac{1}{n+1}\right) \leq g_n \left( a_n \right) \leq g_n \left( \frac{1}{n}\right) $

$\displaystyle g_n \left(\frac{1}{n}\right)h_n \left(\frac{1} {n+1}\right) \leq g_n \left( a_n \right) h_n (a_n )=f_n (a_n )\leq g_n \left( \frac{1}{n+1}\right)g_n \left( \frac{1}{n}\right) ~~~\cdots\cdots~(\ast)$

한편
$\displaystyle \begin{align}\lim_{n \rightarrow \infty} g_n \left(\frac{1}{n}\right) &= \lim_{n \rightarrow \infty} \frac{n}{n} \left(1- \frac{1}{n}\right)^n \\&=\lim_{n \rightarrow \infty} \left\{ \left( 1- \frac{1}{n}\right)^{-n} \right\}^{-1}\\&=e^{-1}=\frac{1}{e}\end{align}$,
$\displaystyle \begin{align}\lim_{n \rightarrow \infty} g_n \left(\frac{1}{n+1}\right) &= \lim_{n \rightarrow \infty} \frac{n}{n+1} \left(1- \frac{1}{n+1}\right)^n \\&=\lim_{n \rightarrow \infty} \frac{n}{n+1} \left\{ \left( 1- \frac{1}{n+1}\right)^{-n-1} \right\}^{-1}\\&=\lim_{n \rightarrow \infty} \frac{n}{n+1} \lim_{n \rightarrow \infty}\left\{ \left( 1- \frac{1}{n+1}\right)^{-n-1} \right\}^{-1}\\&=1\times e^{-1}=\frac{1}{e}\end{align}$
또,
$\displaystyle \begin{align}\lim_{n \rightarrow \infty} h_n \left(\frac{1}{n}\right) &= \lim_{n \rightarrow \infty} \frac{1}{1+\left(n \times \frac{1}{n} -1 \right)^2} =1\end{align}$,
$\displaystyle \begin{align}\lim_{n \rightarrow \infty} h_n \left(\frac{1}{n+1}\right) &= \lim_{n \rightarrow \infty} \frac{1}{1+\left(n \times \frac{1}{n+1} -1 \right)^2}\\&= \lim_{n \rightarrow \infty} \frac{1}{1+\left( -\frac{1}{n+1} \right)^2} =1\end{align}$
이를 이용하여 $\displaystyle \ast$의 좌변, 우변의 극한을 구하면 $\displaystyle \frac{1}{e}$이다.
따라서 $\displaystyle \lim_{n \rightarrow\infty} f_n (a_n)=\frac{1}{e}$

저작자표시 비영리 변경금지