[더플러스수학학원] 울산과고 1학년 2학기 기말대비-미적분 극한~평균값정리 서술형 문제 [울산과학고]

1. 함수 $\displaystyle f ( x) $가 임의의 실수 $\displaystyle x,~y $에 대하여

$$\displaystyle f ( x+y)=f ( x)+f ( y)+xy $$

를 만족시킨다. 다음을 보여라.

(1) 함수 $\displaystyle f ( x) $가 $\displaystyle x=0 $에서 연속이면 $\displaystyle f ( x) $는 모든 실수에서 연속임을 보여라.

(2) $\displaystyle f ' ( 0)=1 $이라 할 때, $\displaystyle f ( x) $가 모든 실수에서 미분가능함을 보이고 도함수 $\displaystyle f ' ( x) $를 구하여라.

 

정답 및 풀이

(1) \(\displaystyle f ( x+y)=f ( x)+f ( y)+xy ~~\cdots\cdots~(\mathrm{i})\)

(i)의 식에서 \(\displaystyle x=y=0\)을 대입하면

\(\displaystyle f(0)=f(0)+f(0)+0~~~\therefore~f(0)=0\)

함수 \(\displaystyle f(x)\)가 \(\displaystyle x=0\)에서 연속이라 가정하면

\(\displaystyle \lim\limits_{h \rightarrow 0} f(h)=f(0)=1~~\cdots\cdots~(\mathrm{ii})\)

\(\displaystyle f(x)\)가 모든 실수 \(\displaystyle x\)에서 연속임을 보이려면 \(\displaystyle \mathrm{(i),~(ii)}\)를 이용하여 다음을 보이면 된다.

\(\displaystyle \lim\limits_{h \rightarrow 0} f(x+h)=f(x) \)

\(\displaystyle \begin{align} \lim\limits_{h \rightarrow 0} f(x+h)&= \lim\limits_{h \rightarrow 0} f(x)+f(h)+xh \\&= \lim\limits_{h \rightarrow 0} f(x)+\lim\limits_{h \rightarrow 0} f(h)+\lim\limits_{h \rightarrow 0} xh \\&= f(x)+f(0)+0\\&= f(x)\end{align}\)

\(\displaystyle \therefore\) \(\displaystyle f(x)\)는 모든 실수에서 연속이다.

(2) \(\displaystyle f'(0)=1\)이므로

\(\displaystyle f'(0)=\lim\limits_{h \rightarrow 0} \frac{f(0+h)-f(0)} {h} = \lim\limits_{h \rightarrow 0} \frac{f(h))} {h}=1 \)

\(\displaystyle \begin{align} \therefore~ f'(x)&=\lim\limits_{h \rightarrow 0} \frac{f(x+h)-f(x)} {h} \\&= \lim\limits_{h \rightarrow 0} \frac{f(x)+f(h)+xh-f(x)} {h}\\&= \lim\limits_{h \rightarrow 0} \frac{f(h)}{h}+x=f'(0)+x\\&=x+1 \end{align} \)

\(\displaystyle \therefore\) \(\displaystyle f(x)\)는 모든 실수에서 미분가능하고 도함수 \(\displaystyle  f'(x)\)는

\(\displaystyle f'(x)=x+1 \)

이다.

 

 

 

2. 다음 함수의 그래프를 그리고, 연속성을 조사하여라.

(1) $\displaystyle f ( x)= \lim\limits _ {n \rightarrow \infty } { \frac {x ^ {n} +x} {x ^ {n} +1} } $

(2) $\displaystyle f ( x)= \sum\limits _ {n=1} ^ {\infty } \frac {x ^ {2} } {\left ( 1+x ^ {2} \right ) ^ {n-1} } $

 

(풀이)

(1) $\displaystyle x \neq -1 $인 모든 점에서 연속

(2) $\displaystyle x \neq 0 $인 모든 점에서 연속

(1) (i) \(\displaystyle | x| <1\)일 때,

$\displaystyle \begin{align}f ( x)&= \lim\limits _ {n \rightarrow \infty } { \frac {x ^ {n} +x} {x ^ {n} +1} } \\& =x \end{align}$

(ii)  \(\displaystyle | x| >1\)일 때,

$\displaystyle \begin{align}f ( x)&= \lim\limits _ {n \rightarrow \infty } \frac {x ^ {n} +x} {x ^ {n} +1} \\& = \lim\limits _ {n \rightarrow \infty } \frac{1+ \frac{1}{x^{n-1}}}{1+\frac{1}{x^n}}=1 \end{align}$

(iii) \(\displaystyle x=1\)일 때, \(\displaystyle f(1)= 1\)

(iv) \(\displaystyle x=-1\)일 때, 정의되지 않음

따라서 함수 \(\displaystyle f(x)\)의 그래프를 그리면 아래와 같다. 

따라서 $\displaystyle x \neq -1 $인 모든 점에서 연속이다.

(2) \(\displaystyle f(x)\)를 나열하면

\(\displaystyle f(x)= x^2 + \frac{x^2}{1+x^2 }+ \frac{x^2 }{(1+x^2 )^2}+\frac{x^2 }{(1+x^2 )^3}+ \cdots\)

\(\displaystyle f(x)\)는 등비급수이므로 공비 \(\displaystyle r\)은

\(\displaystyle r=\frac{1} {1+x^2 } \)

이다.

(i) \(\displaystyle x \neq 0\)이면 \(\displaystyle -1<r<1\)이므로 수렴하고 그 값은

\(\displaystyle \begin{align} f(x)&= \frac{x^2}{1- \frac{1}{1+x^2}} \\&= 1+x^2 \end{align}\)

(ii) \(\displaystyle x=0\)이면 \(\displaystyle f(0)= 0\)이다. 

따라서 함수 \(\displaystyle f(x)\)의 그래프를 그리면 아래와 같다. 

 위의 그림에서 보듯이 함수 \(\displaystyle f(x)\)는 $\displaystyle x \neq 0 $인 모든 점에서 연속이다.

 

 

 

3. 모든 실수에서 연속인 함수 $\displaystyle f ( x) $가 $\displaystyle \left ( e ^ {2x} -1 \right ) f ( x)=\sin 3x $를 만족할 때, $\displaystyle f ( 0) $의 값을 구하여라.

 

 

(풀이)

정답 $\displaystyle \frac {3} {2} $

 

(풀이)

$\displaystyle \left ( e ^ {2x} -1 \right ) f ( x)=\sin 3x $에서 \(\displaystyle f(x)\)는 \(\displaystyle  e^{2x}-1 \neq 0\)일 때, 즉 \(\displaystyle x \neq 0\)일 때, 

$$\displaystyle  f ( x)=\frac {\sin 3x}{  e ^ {2x} -1  }$$

\(\displaystyle x = 0\)일 때는 모든 함숫값을 가진다.  즉,

\(\displaystyle f(x)=\begin{cases} \frac{\sin 3x}{e^{2x}-1}&(x \neq 0)\\0&(x=0)\end{cases}\)

그런데 함수 \(\displaystyle f( x) \)는 모든 실수에서 연속이므로 \(\displaystyle x =0\)에서 연속을 만족하면 모든 실수에서 연속이 된다.

따라서

\(\displaystyle \begin{align} \lim\limits_{x \rightarrow 0} f(x)&=\lim\limits_{x \rightarrow 0} \frac{\sin 3x}{e^{2x}-1}\\& =\lim\limits_{x \rightarrow 0} \frac{2x}{e^{2x}-1}\times \frac{\sin 3x}{3x}\times \frac{3}{2}\\&=1\times 1\times \frac{3}{2}=\frac{3}{2}=f(0)\end{align}\)

\(\displaystyle \therefore ~f(0)=\frac{3}{2}\)

 

 

 

4. 다음 조건을 만족하는 상수 $\displaystyle a,~b $의 값을 구하여라.

(1) $\displaystyle \lim\limits _ {x \rightarrow \infty } {\left ( \sqrt {x ^ {2} +4x+1} -ax-1 \right ) =b} $

(2) $\displaystyle \lim\limits _ {x \rightarrow \frac {\pi } {6} } { \frac {\sqrt {a+\cos ^ {2} x} +a} {2\sin x-1} =b} $

 

 

(풀이)

(1) $\displaystyle a=b=1 $ (2) $\displaystyle a=b=- \frac {1} {2} $

 

(1) $\displaystyle \lim\limits _ {x \rightarrow \infty } {\left ( \sqrt {x ^ {2} +4x+1} -ax-1 \right ) =b} ~~\cdots\cdots ~(\mathrm{i})$에서 분자를 유리화하면

$\displaystyle \begin{align} \lim\limits _ {x \rightarrow \infty } {\left ( \sqrt {x ^ {2} +4x+1} -ax-1 \right )} &=\lim\limits _ {x \rightarrow \infty } \frac{x^2 +4x+1-(ax+1)^2 }{\left ( \sqrt {x ^ {2} +4x+1} +ax+1 \right )  }\\&= \lim\limits _ {x \rightarrow \infty } \frac{(1-a^2)x^2 +(4-2a)x }{\left ( \sqrt {x ^ {2} +4x+1} +ax+1 \right )  }=b\end{align} $

여기서 만약 분자의 최고차항의 계수 $\displaystyle 1-a^2$가 $\displaystyle 0$이 아니면 분모는 일차, 분자는 이차식이므로 발산하므로 

$\displaystyle 1-a^2 =0$  $\displaystyle \therefore ~a=\pm1$

$\displaystyle a=-1$이면 \(\mathrm{i}\)에서 극한은 무한대로 발산하므로 

$\displaystyle a=1$

또, 이차항의 계수의 비에서

$\displaystyle \frac{4-2a}{1+a}=\frac{2}{2}=1=b$  $\displaystyle \therefore ~b=1$

 

(2) $\displaystyle \lim\limits _ {x \rightarrow \frac {\pi } {6} } { \frac {\sqrt {a+\cos ^ {2} x} +a} {2\sin x-1} =b} $에서 \(\displaystyle x \rightarrow \frac{\pi}{6}\)이면 \(\displaystyle (분모)\rightarrow 0\)이므로

\(\displaystyle (분자) \rightarrow \sqrt{a+\left(\frac{\sqrt{3}}{2}\right)^2} +a  =0\)  \(\displaystyle \sqrt{a+ \frac{3}{4}}+a=0~~\cdots\cdots ~(\mathrm{i}) ,~ 4a^2 -4a-3=0\)

\(\displaystyle \therefore~a= - \frac{1}{2}\) 또는 \(\displaystyle a= \frac{3}{2}\)

이 중 \(\displaystyle (\mathrm{i})\)을 만족하는 것은 \(\displaystyle a= - \frac{1}{2}\)이다.

이제 \(\displaystyle a= - \frac{1}{2}\)을 $\displaystyle \lim\limits _ {x \rightarrow \frac {\pi } {6} } { \frac {\sqrt {a+\cos ^ {2} x} +a} {2\sin x-1} =b} $에 대입하면

$\displaystyle \lim\limits _ {x \rightarrow \frac {\pi } {6} } { \frac {\sqrt {- \frac{1}{2}+\cos ^ {2} x} -\frac{1}{2}} {2\sin x-1} =b} $

이제 이 극한값을 구해보자.

먼저 \(\displaystyle x- \frac{\pi}{6}= t \)로 치환하면  \(\displaystyle   {x \rightarrow \frac {\pi } {6} }\)이므로 \(\displaystyle  {t \rightarrow 0 }\)

따라서

$\displaystyle \begin{align} \lim\limits _ {x \rightarrow \frac {\pi } {6} }  \frac {\sqrt {- \frac{1}{2}+\cos ^ {2} x} -\frac{1}{2}} {2\sin x-1} &=\lim\limits _ {t \rightarrow 0 }  \frac {\sqrt {- \frac{1}{2}+\cos ^ {2}\left( t+\frac{\pi}{6}\right)} -\frac{1}{2}} {2\sin \left( t+\frac{\pi}{6}\right)-1} \end{align} $

그런데 이 극한은 삼각함수의 덧셈정리를 써서 변형해야 하므로 너무 복잡하다.

다르게 한번 구해보자.

먼저 유리화해서 

$\displaystyle \begin{align} \lim\limits _ {x \rightarrow \frac {\pi } {6} }  \frac {\sqrt {- \frac{1}{2}+\cos ^ {2} x} -\frac{1}{2}} {2\sin x-1} &=\lim\limits _ {x \rightarrow \frac {\pi } {6} }   \frac { - \frac{3}{4}+\cos ^ {2} x}    {(2\sin x-1)\left\{ \sqrt {- \frac{1}{2}+\cos ^ {2} x} +\frac{1}{2}\right\}} \\& =\lim\limits _ {x \rightarrow \frac {\pi } {6} }   \frac { \left(\cos x - \frac{\sqrt3}{2}\right) \left(\cos x+ \frac{\sqrt3}{2}\right)}    {(2\sin x-1)\left( \sqrt {- \frac{1}{2}+\cos ^ {2} x} +\frac{1}{2}\right)} \end{align} $

이 극한을 구하기 위해 먼저 다음의 극한을 미분정의로 풀어 보자.

$\displaystyle \begin{align}\lim\limits _ {x \rightarrow \frac {\pi } {6} }   \frac { \cos x - \frac{\sqrt3}{2}  }    { 2\sin x- 1 }=\lim\limits _ {x \rightarrow \frac {\pi } {6} }   \frac{\frac { \cos x - \frac{\sqrt3}{2}  }  {x - \frac {\pi } {6} }}   { \frac{2\sin x-1}{x - \frac {\pi } {6} } } ~~\cdots\cdots (\mathrm{i})\end{align} $

여기서 분자의 극한값은 $\displaystyle \cos x $를 $\displaystyle x= \frac{\pi}{6}$에서 미분한 미분계수이다. 즉 $\displaystyle -\sin \frac{\pi}{6}= -\frac{1}{2}$

또, 분모의 극한값은 $\displaystyle 2\sin x $를 $\displaystyle x= \frac{\pi}{6}$에서 미분한 미분계수이다. 즉 $\displaystyle 2 \cos \frac{\pi}{6}= \sqrt 3$

따라서 $\displaystyle  (\mathrm{i})$의 극한값은

$\displaystyle \begin{align}\lim\limits _ {x \rightarrow \frac {\pi } {6} }   \frac { \left(\cos x - \frac{\sqrt3}{2}\right) \left(\cos x+ \frac{\sqrt3}{2}\right)}    {(2\sin x-1)\left( \sqrt {- \frac{1}{2}+\cos ^ {2} x} +\frac{1}{2}\right)} &=   \frac{-\frac{1}{2} \times \sqrt3 }   { \sqrt 3 \times \left( \sqrt{\frac{1}{4}}+\frac{1}{2}\right)  }\\&=-\frac{1}{2} \end{align} $

이다.

 

 

 

 

5. $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {1-\cos \left ( 1-\cos 2x \right )} {2 ^ {m} x ^ {n} } = \alpha } $를 만족시키는 자연수 $\displaystyle m,~n,~ \alpha $의 값을 구하여라.

 

 

(풀이)

$\displaystyle m=1 $, $\displaystyle n=4 $, $\displaystyle \alpha =1 $

 

(풀이) $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {1-\cos \left ( 1-\cos 2x \right )} {2 ^ {m} x ^ {n} } = \alpha }   $를 만족하는 자연수 $\displaystyle m,~n,~ \alpha $을 구하기 위해 먼저 다음의 극한을 증명하자.

$\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {1-\cos x} {  x ^ {2} } = \frac{1}{2} } $

(증명) 위의 극한에서 분자 분모에 $\displaystyle  {1+\cos x} $를 곱하고 $\displaystyle \lim\limits _ {x \rightarrow 0}   \frac {\sin x} {  x   } = 1 $임을 이용하면

$\displaystyle \begin{align} \lim\limits _ {x \rightarrow 0}  \frac {1-\cos x} {  x ^ {2} } &=\lim\limits _ {x \rightarrow 0}   \frac {(1-\cos x)(1+\cos x)} {  x ^ {2}(1+\cos x) } \\& =\lim\limits _ {x \rightarrow 0}   \frac {1-\cos^2 x} {  x ^ {2}(1+\cos x)}   \\&=\lim\limits _ {x \rightarrow 0}   \frac {\sin^2 x} {  x ^ {2}} \frac{1}{1+\cos x } \\&= 1^2 \times \frac{1}{2} =\frac{1}{2}  \end{align} $

$\displaystyle \begin{align} &\lim\limits _ {x \rightarrow 0}   \frac {1-\cos \left ( 1-\cos 2x \right )} {2 ^ {m} x ^ {n} } \\&=\lim\limits _ {x \rightarrow 0,~1-\cos2x \rightarrow 0}   \frac {1-\cos \left ( 1-\cos 2x \right )} {\left ( 1-\cos 2x \right )^2}\times \frac{\left ( 1-\cos 2x \right )^2} {(2x)^4}\times \frac {(2x)^4}  {2 ^ {m} x ^ {n} }  \\& =\frac{1}{2}\times \frac{1}{4}\times \frac{2^4}{2^m} =\frac{2}{2^m}=\alpha \end{align}     $

위처럼 변형하면 극한값 \(\displaystyle \alpha\)도 자연수이므로 \(\displaystyle n=4,~m=1,~\alpha =1\)이다.

 

 

 

 

 

6. $\displaystyle \mathrm { \overline {AB}} = a $, $\displaystyle \mathrm { \overline {AC}} = b $, $\displaystyle \mathrm { \angle BAC}= \theta $인 $\displaystyle \mathrm { \triangle ABC} $에서 $\displaystyle \mathrm { \angle BAC }$의 이등분선이 변 $\displaystyle \mathrm { BC }$와 만나는 점을 $\displaystyle \mathrm { D} $, $\displaystyle \mathrm { \overline {AD}} = l $이라고 할 때, 다음 물음에 답하여라.

(1) $\displaystyle l $을 $\displaystyle a,~b,~ \theta $를 써서 나타내어라.

(2) $\displaystyle a,~b $가 일정하다고 할 때, $\displaystyle \lim\limits _ {\theta \rightarrow 0} {l} $의 값을 $\displaystyle a,~b $를 써서 나타내어라.

 

(풀이)

(1) $\displaystyle l= \frac {2ab} {a+b} \cos \frac {\theta } {2} $ (2) $\displaystyle \lim\limits _ {\theta \rightarrow 0} {l} = \frac {2ab} {a+b} $

 

(1) 삼각형 \(\displaystyle \mathrm{ABC}\)의 넓이 \(\displaystyle S\)를 두가지로 표현해보자.

\(\displaystyle \begin{align} S&=\frac{1}{2} a \times b \sin \theta \\&= \frac{1}{2} a \times l \sin \frac{\theta}{2} +\frac{1}{2} l \times b \sin \frac{\theta}{2} \end{align}\)

따라서 \(\displaystyle l\)을 구하면

\(\displaystyle  a \times b \sin \theta =a \times l \sin \frac{\theta}{2} + l \times b \sin \frac{\theta}{2} \)

\(\displaystyle  l= \frac {ab \sin \theta} {(a+b)\sin \frac{\theta}{2}} =\frac{2ab}{a+b}\cos \frac {\theta } {2} \)

(2) \(\displaystyle \theta \rightarrow 0\)이면 \(\displaystyle \cos \frac{\theta}{2} \rightarrow 1\)이므로

\(\displaystyle \lim\limits_{\theta \rightarrow0}  l =  \lim\limits_{\theta \rightarrow 0} \frac{2ab}{a+b}\cos \frac {\theta } {2} = \frac{2ab}{a+b} \)

 

 

 

 

 

 

7. 함수 $\displaystyle f ( x)= \lim\limits _ {n \rightarrow \infty } { \frac {x ^ {2n+1} + \left ( a-1 \right ) x ^ {n} -1} {x ^ {2n} -ax ^ {n} -1} } $이 $\displaystyle x \geq 0 $에서 연속이라고 할 때, 상수 $\displaystyle a $의 값을 구하여라. (단, $\displaystyle a \neq 0 $)

 

 

(풀이)

정답 $\displaystyle \frac {1} {2} $

 

다음 각각의 범위에서 극한값을 구하여  \(\displaystyle f(x) \)의 그래프를 찾아보자.

(i) \(\displaystyle 0 \leq x <1\)일 때

\(\displaystyle \lim\limits _ {n \rightarrow \infty } x^n =0\)

이므로 $\displaystyle f ( x) $는

$\displaystyle f ( x)= \lim\limits _ {n \rightarrow \infty } { \frac {x ^ {2n+1} + \left ( a-1 \right ) x ^ {n} -1} {x ^ {2n} -ax ^ {n} -1} } =1$

(ii) \(\displaystyle x> 1   \)일 때

\(\displaystyle \lim\limits _ {n \rightarrow \infty } x^n = \infty\)

이므로 극한의 분자, 분모를 $\displaystyle x^{2n} $으로 나누면\(\displaystyle \lim\limits _ {n \rightarrow \infty } \frac{1}{x^n} = 0\)이므로 $\displaystyle f ( x) $는

$\displaystyle \begin{align} f ( x) &= \lim\limits _ {n \rightarrow \infty } \frac {x ^ {2n+1} + \left ( a-1 \right ) x ^ {n} -1} {x ^ {2n} - ax ^ {n} -1}  \\&=\lim\limits _ {n \rightarrow \infty }  \frac {x  +  \frac{\left ( a-1 \right )} {x ^ {n}} - \frac{1}  {x ^ {2n}}} {1-\frac{a}{x^n}-\frac{1}{x^{2n}}}   =x\end{align}$

(i) \(\displaystyle  \leq x =1\)일 때

\(\displaystyle f(1)=\frac{a-1}{-a}=\frac{1-a}{a}\)

따라서 (i), (ii), (iii)에 의해 \(\displaystyle f(x)\)는

\(\displaystyle \begin{align} f(x)=\begin{cases} 1&(0 \leq x<1일~때)\\ \frac{1-a}{a}&(x=1일~때)\\x&(x >1일~때)\end{cases} \end{align}\)

함수 \(\displaystyle f(x)\)가 \(\displaystyle x\)가 \(\displaystyle  0\)이상에서 연속하므로 \(\displaystyle x=1\)에서 연속이면 된다. 따라서

\(\displaystyle f(1)=\lim\limits_{x \rightarrow 1+} f(x)= \lim\limits_{x \rightarrow 1-}f(x) \)

\(\displaystyle \frac{1-a}{a}=\lim\limits_{x \rightarrow 1+} x= \lim\limits_{x \rightarrow 1-}1\)

\(\displaystyle \therefore ~ a= \frac{1}{2}\)

 

 

 

 

 

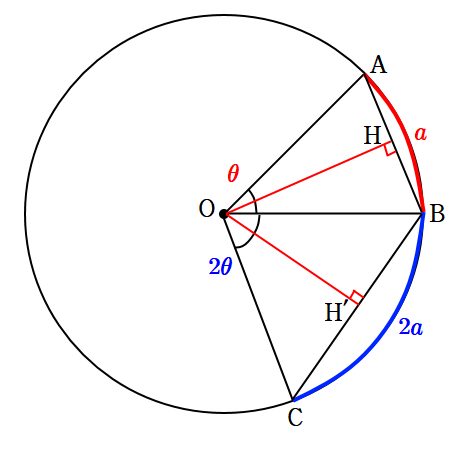
8. 어떤 원 위의 세 점 $\displaystyle \mathrm { A,~B,~C} $에 대하여 호 $\displaystyle \mathrm { AB }$, 호 $\displaystyle \mathrm { BC} $의 길이를 각각 $\displaystyle a,~2a $라 하고 현 $\displaystyle \mathrm { AB }$, 현 $\displaystyle \mathrm { BC }$의 길이를 각각 $\displaystyle b,~c $라고 할 때, $\displaystyle \lim\limits _ {a \rightarrow 0} { \frac {b+c} {a} } $의 값을 구하여라.

 

(풀이)

$\displaystyle 3 $

 

 

 

 

 

 

 

 

 

9. 미분가능한 함수 $\displaystyle f ( x),~g ( x) $에 대하여 $\displaystyle y=f ( x)g ( x) $일 때, $\displaystyle y ' =f ' ( x)g ( x)+f ( x)g ' ( x) $임을 증명하여라.

 

(풀이)

생략 미분정의를 이용하여 풀면 된다. 

 

 

 

 

10. 항상 양의 값을 갖는 함수 $\displaystyle f ( x) $가 임의의 실수 $\displaystyle x,~y $에 대하여

$$\displaystyle f \left ( x+y \right ) =2f ( x)f ( y) $$

인 관계를 만족시킬 때, 다음 물음에 답하여라. [중앙대]

(1) $\displaystyle f ( 0) $의 값을 구하여라.

(2) $\displaystyle f ' ( 0)=a $일 때, $\displaystyle f ' ( x) $를 $\displaystyle a $와 $\displaystyle f ( x) $를 써서 나타내어라.

 

 

(풀이)

정답 (1) $\displaystyle f ( 0)= \frac {1} {2} $

(2) $\displaystyle f ' ( x)=2af ( x) $

(1) \(\displaystyle f \left ( x+y \right ) =2f ( x)f ( y) ~~\cdots\cdots~(\mathrm{i})\)

\((\mathrm{i})\)에 \(\displaystyle x=y=0\)을 대입하면

$\displaystyle f \left ( 0+0 \right ) =2f ( 0)f ( 0) $   $\displaystyle f \left (0\right ) =2\left\{f (0)\right\}^2 $

$\displaystyle f \left ( x \right )>0 $이므로 $\displaystyle f \left ( 0 \right ) =\frac{1}{2}$

(2) $\displaystyle f \left ( 0 \right ) =\frac{1}{2}$를 이용하여 미분정의로 $\displaystyle f' \left ( 0 \right )$를 구하면

$\displaystyle \begin{align} f' \left ( 0 \right ) &=\lim\limits_{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}\\&= \lim\limits_{h \rightarrow0} \frac{f(h)-1}{h}=a \end{align}$

$\displaystyle \therefore~f' \left ( 0 \right ) = \lim\limits_{h \rightarrow0} \frac{f(h)-1}{h}=a ~~\cdots\cdots ~(\mathrm{ii}) $

\((\mathrm{i})\)과 \((\mathrm{ii})\)를 이용하여 \(\displaystyle f'(x)\)를 구해보면

$\displaystyle \begin{align} f' \left ( x \right ) &=\lim\limits_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\\&= \lim\limits_{h \rightarrow0} \frac{2f(x)f(h)-f(x)}{h}\\& =\lim\limits _{h \rightarrow 0} \frac{2f(x) \left\{ f(h)- \frac{1}{2} \right\}}{h}\\&=2f(x) \lim\limits_{h \rightarrow0} \frac{f(h)-\frac{1}{2}} {h} \\& =2 f(x)f'(0)=2af(x) \end{align}$

 

 

 

 

11. 함수 $\displaystyle f ( x) $가 $$\displaystyle f ( x)= { \begin {cases}  x \left ( \frac {1} {2}  -x\sin \frac {1} {x} \right ) & \left ( x \neq 0 \right )\\~0 & \left ( x=0 \right )\end {cases} } $$

으로 정의될 때, 다음 물음에 답하여라.

(1) $\displaystyle f ' \left ( 0 \right ) $의 값을 구하여라.

(2) $\displaystyle \sin \frac {1} {x} =0 $, $\displaystyle \cos \frac {1} {x} < 0 $를 만족하는 $\displaystyle x $의 값에 대하여 $\displaystyle f ' ( x) $의 값을 구하여라.

 

 

(풀이)

(1) $\displaystyle f ' ( 0)= \frac {1} {2} $

(2) $\displaystyle - \frac {1} {2} $

(풀이)

(1) 먼저 \(\displaystyle \lim\limits _{h \rightarrow0} h \sin \frac{1}{h}=0\)임을 보이자.

\(\displaystyle 0\leq \left| \sin \frac{1}{h} \right| \leq 1\)

이므로 양변에 \(\displaystyle |h| (\geq 0)\)를 곱하면

\(\displaystyle 0\leq \left| h \sin \frac{1}{h} \right| \leq \left| h \right|\)

여기서 \(\displaystyle \lim\limits _{h \rightarrow0} |h|=0\)이므로

\(\displaystyle \lim\limits _{h \rightarrow0} h \sin \frac{1}{h}=0\)

이다. 이 성질을 이용하여 \(\displaystyle x=0\)에서의 미분계수를 구하면

\(\displaystyle \begin{align} f'(0) &=\lim\limits _{h \rightarrow0} \frac{f(0+h)-f(0)}{h}\\&=\lim\limits_{h \rightarrow0} \frac{h \left( \frac{1}{2} -h \sin \frac{1}{h} \right) -0}{h}\\&=\lim\limits_{h \rightarrow0} \left( \frac{1}{2} - h \sin \frac{1}{h} \right) \\&=\frac{1}{2} \end{align}\)

즉,

$\displaystyle f ' ( 0)= \frac {1} {2} $

(2) 함수 \(\displaystyle f  (x)\)는 모든 실수에서 미분가능하므로 도함수를 구하면

(1)에서 $\displaystyle f ' ( 0)= \frac {1} {2} $

$\displaystyle x \neq 0 $에서는 

$\displaystyle \begin{align} f ' ( x) &= \frac{1}{2} -x \sin \frac{1}{x} + x \left( 0- \sin \frac{1}{x} - x \cos \frac{1}{x} \times \left(- \frac{1}{x^2}\right) \right)\\&=\frac{1}{2} -2x \sin \frac{1}{x}+ \cos \frac{1}{x}  \end{align} ~~\cdots\cdots~(\mathrm{i})$

한편 $\displaystyle \sin \frac {1} {x} =0 $, $\displaystyle \cos \frac {1} {x} < 0 $이면 \(\displaystyle \frac{1}{x}=2n \pi + \frac{3}{2} \pi \) (\(n\)은 정수)이므로

$\displaystyle \cos \frac {1} {x} = -1 $, $\displaystyle \sin \frac {1} {x} = 0 $

이다. 따라서 (\(\mathrm{i}\))에서 

$\displaystyle f ' ( x) = \frac{1}{2} -1=-\frac{1}{2}$

 

 

 

12. 미분가능한 함수 $\displaystyle f ( x) $에 대하여 $\displaystyle f \left ( 1 \right ) =2,~f ' \left ( 1 \right ) =1 $일 때, $\displaystyle \lim\limits _ {x \rightarrow 1} { \frac {f \left ( x ^ {3} \right ) -2x ^ {3} } {x ^ {2} -1} } $의 값을 구하여라.

 

 

 

13. 함수 $\displaystyle f \left ( x \right ) = \left ( x-a \right ) \left ( x-b \right ) \left ( x-c \right ) $ ($\displaystyle a,~b,~c $는 서로 다른 상수)에 대하여

$$\displaystyle \frac {a ^ {3} } {f ' \left ( a \right )} + \frac {b ^ {3} } {f ' \left ( b \right )} + \frac {c ^ {3} } {f ' \left ( c \right )} $$

을 간단히 하여라.

 

 

 

 

 

14. 다음 물음에 답하여라.

(1) $\displaystyle n $이 정수일 때, $\displaystyle \left ( x ^ {n} \right ) ' =nx ^ {n-1} $이다. 이를 이용하여 $\displaystyle r $가 유리수일 때, $\displaystyle \left ( x ^ {r} \right ) ' =rx ^ {r-1} $임을 증명하여라.

(2) 함수 $\displaystyle f \left ( x \right ) = \frac {1} {\sqrt {x ^ {2} +1} } $을 미분하여라.

 

 

 

 

 

15. 항등적으로 $\displaystyle 0 $이 아닌 함수 $\displaystyle f ( x) $가 임의의 $\displaystyle x,~y $에 대하여 등식

$$\displaystyle f \left ( x+y \right ) =f ( x)f ( y) $$

를 만족할 때, 다음을 증명하여라.

(1) 임의의 실수 $\displaystyle x $에 대하여 $\displaystyle f ( x)>0 $이다.

(2) $\displaystyle f ( 0)=1 $

(3) $\displaystyle x=a $에서 $\displaystyle f ( x) $가 연속이면 $\displaystyle f ( x) $는 임의의 $\displaystyle x $에서 연속이다.

(4) $\displaystyle f ' ( 0) $가 존재하고 $\displaystyle f ' ( 0)=a $이면, $\displaystyle f ' ( x) $가 존재하고 $\displaystyle f ' ( x)=af ( x) $이다.

 

정답 및 풀이

---

(1) \(\displaystyle f \left ( x+y \right ) =f ( x)f ( y) ~~\cdots\cdots~(\mathrm{i})\)

\((\mathrm{i})\)에 \(\displaystyle x,~y\) 대신에  각각 \(\displaystyle \frac{x}{2},~\frac{x}{2}\)를 대입하면

$\displaystyle f(x)=f \left ( \frac{x}{2}+\frac{x}{2} \right ) =\left\{f ( x) \right\}^2 \geq 0$ 

이제 등호가 성립하지 않음을 보이자. 귀류법으로 $\displaystyle f \left (x_0 \right ) =0 $인 \(\displaystyle x_0\)가 존재한다고 가정하면

$\displaystyle \begin{align} f(x) &=f \left ( x_0 +(x-x_0 )\right ) \\&=f ( x_0 )f(x-x_0 ) \\&=0 \times f(x-x_0 ) =0\end{align}$ 

즉 모든 실수에 대하여 $\displaystyle f(x) =0$이므로 항등적으로 $\displaystyle 0$이 아니라는 가정에 모순이다. 따라서   

$$\displaystyle f ( x)>0 $$

(2) \((\mathrm{i})\)의 \(\displaystyle x,~y\) 대신에  각각 \(\displaystyle x=0,~y=0\)을 대입하고 (1)에서 $\displaystyle f ( x)>0 $임을 이용하면

$\displaystyle  f \left ( 0+0 \right ) =\left\{f(0)\right\}^2 $, $\displaystyle  f (0)=0 ~또는 ~1$

$\displaystyle \therefore~f(0)=1$

(3) 먼저 $\displaystyle x=a$에서 연속이면 $\displaystyle x=0$에서 연속임으로 보이자.

$\displaystyle x=a$에서 연속이고 $\displaystyle f(x)>0$므로

$\displaystyle \begin{align} f(0)&=1=\frac{f(a)}{f(a)}=\frac{\lim\limits_{h \rightarrow0} f(a+h)}{f(a)} \\&=\frac{\lim\limits_{h \rightarrow0} f(a)\times f(h)}{f(a)}\\&=\frac{f(a)\times  \lim\limits_{h \rightarrow 0}  f(h)}{f(a)}\\&= \lim\limits_{h \rightarrow0} f(h)\end{align}$

즉, $\displaystyle   f(0)= \lim\limits_{h \rightarrow0} f(h) $

따라서 함수 $\displaystyle f$는 $\displaystyle x=0$에서 연속이다. $\displaystyle x=0$에서 연속임을 이용하여, 즉, $\displaystyle   f(0)= \lim\limits_{h \rightarrow0} f(h) $

임의의 실수 $\displaystyle x$에서 연속임을 다음과 같이 보일 수 있다.

$\displaystyle \begin{align}  \lim\limits_{h \rightarrow 0}  f(x+h) &= \lim\limits_{h \rightarrow0} f(x)f(h)\\& =f(x) \lim\limits _{h \rightarrow 0} f(h)\\&=f(x)f(0)=f(x) \times 1\\&=f(x) \end{align}$

(4) $\displaystyle f \left ( 0 \right ) =1$를 이용하여 미분정의로 $\displaystyle f' \left ( 0 \right )$를 구하면

$\displaystyle \begin{align} f' \left ( 0 \right ) &=\lim\limits_{h \rightarrow 0} \frac{f(0+h)-f(0)}{h}\\&= \lim\limits_{h \rightarrow0} \frac{f(h)-1}{h}=a \end{align}$

$\displaystyle \therefore~f' \left ( 0 \right ) = \lim\limits_{h \rightarrow0} \frac{f(h)-1}{h}=a ~~\cdots\cdots ~(\mathrm{ii}) $

\((\mathrm{i})\)과 \((\mathrm{ii})\)를 이용하여 \(\displaystyle f'(x)\)를 구해보면

$\displaystyle \begin{align} f' \left ( x \right ) &=\lim\limits_{h \rightarrow 0} \frac{f(x+h)-f(x)}{h}\\&= \lim\limits_{h \rightarrow0} \frac{f(x)f(h)-f(x)}{h}\\& =\lim\limits _{h \rightarrow 0} \frac{f(x) \left\{ f(h)- 1 \right\}}{h}\\&=f(x) \lim\limits_{h \rightarrow0} \frac{f(h)-1} {h} \\& = f(x)f'(0)=af(x) \end{align}$

---

 

 

 

 

16. 구간 $\displaystyle [-1,~1] $에서 정의된 함수 $\displaystyle f ( x) $와 $\displaystyle g ( x) $가 $\displaystyle |g ( x)| \leq f ( x) $를 만족한다. 함수 $\displaystyle f ( x) $가 열린구간 $\displaystyle \left ( -1,~1 \right ) $에서 미분가능하고 $\displaystyle f ( 0)=0 $이면 $\displaystyle g ' ( 0)=0 $임을 보여라.

 

정답 및 풀이

$\displaystyle |g ( x)| \leq f ( x) ~\cdots\cdots ~(\mathrm{i})$이므로 \(\displaystyle f(x) \geq 0 \)이다.

따라서 $\displaystyle (\mathrm{i})$의 절댓값을 풀면

$\displaystyle -f(x) \leq g ( x) \leq f ( x) ~\cdots\cdots~(\mathrm{ii})$

또 $\displaystyle (\mathrm{i})$의 $\displaystyle x$에 $\displaystyle 0$을 대입하면

$\displaystyle |g ( 0)| \leq f ( 0) =0$

$\displaystyle \therefore~ g(0)=0 $

첫째 $\displaystyle x>0 $일 때, \(\displaystyle (\mathrm{ii})\)의 양변을 $\displaystyle x $로 나누고 $\displaystyle f(0)=0,~ g(0)=0 $임을 이용하면

$\displaystyle -\frac{f(x)}{x} \leq \frac{g ( x)}{x} \leq \frac{f ( x)}{x} ~\cdots\cdots~(\mathrm{iii})$

\(\displaystyle x=0\)에서 함수 \(\displaystyle f(x)\)가 미분가능고 \(\displaystyle f(0)=0\)이므로 미분정의에 의해

\(\displaystyle f'(0)=\lim\limits _{x \rightarrow 0+} \frac{f(x)-f(0)}{x-0}=\lim\limits _{x \rightarrow 0+} \frac{f(x)}{x}\)

이다. 따라서 $\displaystyle (\mathrm{iii})$은 

$\displaystyle -f'(0) \leq g'(0) \leq f'(0) $     

위의 부등식으로부터

$\displaystyle -f'(0) \leq  f'(0) ~~f'(0) \geq0$

둘째 $\displaystyle x<0 $일 때, 위의 과정과 똑같이 하면

$\displaystyle -\frac{f(x)}{x} \geq \frac{g ( x)}{x} \geq \frac{f ( x)}{x} ~\cdots\cdots~(\mathrm{iv})$

\(\displaystyle x=0\)에서 함수 \(\displaystyle f(x)\)가 미분가능고 \(\displaystyle f(0)=0\)이므로 미분정의에 의해

\(\displaystyle f'(0)=\lim\limits _{x \rightarrow 0-} \frac{f(x)-f(0)}{x-0}=\lim\limits _{x \rightarrow 0-} \frac{f(x)}{x}\)

이다. 따라서 $\displaystyle (\mathrm{iv})$은 

$\displaystyle -f'(0) \geq g'(0) \geq f'(0) $     

위의 부등식으로부터

$\displaystyle -f'(0) \geq  f'(0) ~~f'(0) \geq0$

첫째, 둘째로부터

$\displaystyle f'(0) \geq 0,~ f'(0) \leq0~~\therefore~f'(0)=0~\therefore~g'(0)=0$

 

 

 

 

 

 

17.$\displaystyle 0 < x < \frac {\pi } {2} $에서 정의된 함수 $\displaystyle f ( x)=\sin x $의 역함수를 $\displaystyle g \left ( x \right ) $라고 할 때,

(1) $\displaystyle g ' \left ( \frac {1} {2} \right ) $의 값을 구하여라.

(2) $\displaystyle g '' \left ( \frac {1} {2} \right ) $의 값을 구하여라.

 

정답 및 풀이

(1) $\displaystyle g ' \left ( \frac {1} {2} \right )=\frac{2}{\sqrt3} $

(2) $\displaystyle g '' \left ( \frac {1} {2} \right )=\frac{4}{3\sqrt3} $

(1) $\displaystyle g \left ( \frac{1}{2} \right ) =a$에서 $\displaystyle f ( a)=\sin a =\frac{1}{2}$

\(\displaystyle a \in \left( 0,~ \frac {\pi}{6}\right)\)이므로 \(\displaystyle \therefore~a= \frac{\pi}{2}\)

따라서 역함수의 미분법에 의해

$\displaystyle \begin{align} g ' \left ( \frac {1} {2} \right )&=\frac{1}{f' \left( \frac{\pi}{6}\right)} =\frac{1}{ \cos \left( \frac{\pi}{6}\right)} \\&=\frac{2}{\sqrt3} \end{align}$

(2) $\displaystyle y=g(x) ~\Longleftrightarrow ~ x=f(y)$에서

$\displaystyle g'(x)= \frac{1}{f'(y)} = \frac{1}{\cos y }$

이 식의 양변을 $\displaystyle x $에 대하여 미분하면

$\displaystyle \begin{align}g'(x) &= \frac{d}{dx}\frac{1}{f'(y)}= \frac{d}{dy}\frac{1}{f'(y)} \frac{dy}{dx}\\&=- \frac{f''(y)}{\left\{f'(y)\right\}^2} \times \frac{1}{f'(y)} \\&= - \frac{-\sin y}{\cos ^2 y} \times \frac{1}{\cos y} \\&=\frac{ \sin y }{\cos^3 y}\end{align}$

\(\displaystyle \begin{align} \therefore ~g'' \left(\frac{1}{2} \right) &= \frac{\sin \frac{\pi}{6}}{ \cos ^3 \frac{\pi}{6}} =\frac{1}{2}\times \left( \frac{2}{\sqrt 3}\right)^3  \\&= \frac{4}{3\sqrt3}\end{align}\)

 

 

18. 다음 물음에 답하여라.

(1) $\displaystyle f ( x)=x ^ {x} e ^ {x} $ ($\displaystyle x>0 $)일 때, $\displaystyle f '' ( 1) $의 값을 구하여라.

(2) $\displaystyle x=\cos \theta + \theta \sin \theta $, $\displaystyle y=\sin \theta - \theta \cos \theta $일 때, $\displaystyle \theta = \frac {\pi } {3} $에서 $\displaystyle \frac {d ^ {2} y} {dx ^ {2} } $의 값을 구하여라.

 

(1) 먼저 $\displaystyle y=x^x $을 로그미분법을 이용하여 도함수를 구해보자. 

양변에 로그(\(\displaystyle \ln\))을 취하여 미분해 보면

$\displaystyle \ln y =\ln x^x ~~~\ln y = x \ln x$

$\displaystyle \frac{d}{dx} \ln y = \frac{d}{dx} \left\{x \ln x\right\}$

$\displaystyle \frac{1}{y} \frac{dy}{dx} =  \ln x + x \times \frac{1}{x} $

$\displaystyle  \frac{dy}{dx} =  y \left(1+ \ln x \right)=x^x \left( 1+ \ln x \right)$

이제 $\displaystyle f'(x)$를 구해보면

$\displaystyle \begin{align}f'(x) &= \left(x^x \right)' e^x + x^x \times (e^x )' \\&= x^x \left( 1+\ln x \right) e^x +x^x e^x \\&= e^x x^x (2+ \ln x)\end{align}$

$\displaystyle \therefore ~f'(x) = e^x x^x (2+ \ln x) $

또, 곱 미분을 이용하여 한번 더 미분하면

$\displaystyle \begin{align}f''(x) &= e^x \times x^x (2+ \ln x) \\&+ e^x \times x^x (2+\ln x )(2+ \ln x )+ e^x x^x \times \frac{1}{x}  \\&= x^x e^x \left(2+ \ln x+ (2+ \ln x )^2  + \frac{1}{x}  \right) \end{align}$

여기에 $\displaystyle  1$을 대입하여 $\displaystyle f''(1)$을 구하면

$\displaystyle f''(1)=7e$

(2) $\displaystyle x=\cos \theta + \theta \sin \theta $, $\displaystyle y=\sin \theta - \theta \cos \theta $에서

$\displaystyle \begin{align}\frac{dy}{dx}&= \frac{\frac{dy}{d \theta}}{\frac{dx}{d \theta}}\\&= \frac{\cos \theta- \cos \theta +\theta \sin \theta}{- \sin \theta +\sin \theta +\theta cos \theta}=\frac{\theta \sin \theta}{\theta \cos \theta}\\&= \frac{\sin \theta}{\cos \theta}=\tan \theta\end{align}$

이제 두 번 미분해보자.

$\displaystyle \begin{align}\frac{d^2 y}{dx^2}&= \frac{d}{dx}\left(\frac{dy}{dx} \right)=\frac{d}{dx}\left(\tan \theta\right) \\&= \frac{\frac{d}{d \theta}\tan \theta}{\frac{dx}{d \theta}} \\&= \frac{\sec^2 \theta}{\theta \cos \theta}\end{align}$

$\displaystyle \therefore~\frac{d^2 y}{dx^2}= \frac{\sec^3 \theta }{\theta }$

따라서 $\displaystyle \theta = \frac {\pi } {3} $에서 $\displaystyle \frac {d ^ {2} y} {dx ^ {2} } $의 값을 구하면

$\displaystyle \begin{align} \left. \frac {d ^ {2} y} {dx ^ {2} } \right|_{\frac{\pi}{3}}&=\frac{\sec^3 \frac{\pi}{3}}{\frac{\pi}{3}}\\&= 8 \times \frac{3}{\pi} = \frac{24}{\pi}\end{align}$

 

 

 

 

 

 

19. 다음 물음에 답하여라. [홍익대]

(1) $\displaystyle f \left ( x \right ) =x ^ {10} +x ^ {5} +3 $을 $\displaystyle \left ( x+1 \right ) ^ {2} $으로 나누었을 때의 나머지를 구하여라.

(2) $\displaystyle ax ^ {4} +bx ^ {3} +1 $이 $\displaystyle \left ( x-1 \right ) ^ {2} $으로 나누어 떨어질 때, 상수 $\displaystyle a,~b $의 값을 구하여라.

(3) $\displaystyle x ^ {10} +x ^ {3} +ax ^ {2} +bx+c $가 $\displaystyle \left ( x-1 \right ) ^ {3} $으로 나누어 떨어지도록 상수 $\displaystyle a,~b,~c $의 값을 정하여라.

 

 

 

 

 

20. 함수 $\displaystyle f \left ( x \right ) = { \begin {cases} x ^ {2} \sin \frac {1} {x} & ( x \neq 0)\\~0 & \left ( x=0 \right )\end {cases} } $에 대하여

(1) $\displaystyle x=0 $에서 $\displaystyle f ( x) $의 미분가능성을 조사하고 만약 미분가능하다면 $\displaystyle f ' ( 0) $의 값을 구하여라.

(2) $\displaystyle x \neq 0 $일 때, $\displaystyle f ( x) $의 도함수 $\displaystyle f ' ( x) $를 구하여라.

(3) $\displaystyle x=0 $에서 $\displaystyle f ' ( x) $의 연속성을 조사하여라.

 

 

 

 

21. $\displaystyle - \frac {\pi } {2} < x < \frac {\pi } {2} $에서 정의된 함수 $\displaystyle f ( x)=\tan x $의 역함수를 $\displaystyle g ( x) $라고 할 때, $\displaystyle g \left ( x \right ) $의 도함수 $\displaystyle g ' \left ( x \right ) $를 $\displaystyle x $에 관한 식으로 나타내어라.

 

 

 

 

22. $\displaystyle x=0 $에서 미분가능한 함수 $\displaystyle f ( x) $에 대하여 $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {f \left ( \sin 8x \right ) -f \left ( \tan x \right )} {x} } $의 값을 $\displaystyle f ' ( 0) $을 써서 나타내어라.

 

 

 

 

23. $\displaystyle x ^ {2} +2xy-y ^ {2} =1 $에서 $\displaystyle \frac {d ^ {2} y} {dx ^ {2} } $를 $\displaystyle x,~y $에 대한 식으로 나타내어라.

 

 

 

 

24. 식 $\displaystyle e ^ {y} +\ln \cos x=1 $에서 $\displaystyle \frac {dy} {dx} ,~ \frac {d ^ {2} y} {dx ^ {2} } $를 구하여라. [연세대]

 

 

 

 

 

접선과 평균값의 정리

 

25. $\displaystyle 0 < x < y < z < \pi $일 때, 평균값의 정리를 이용하여 부등식

$$\displaystyle \frac {\sin y-\sin x} {y-x} > \frac {\sin z-\sin y} {z-y} $$

가 성립함을 증명하여라.

 

 

 

 

26. 포물선 $\displaystyle y=x ^ {2} $ 위에 원점이 아닌 동점 $\displaystyle \mathrm { P} $가 있다. 점 $\displaystyle \mathrm { P} $에서의 이 곡선의 법선이 $\displaystyle y $축과 만나는 점을 $\displaystyle \mathrm { Q} $라고 할 때, 점 $\displaystyle \mathrm { P} $가 원점 $\displaystyle \mathrm { O} $에 한없이 가까이 갈 때, 점 $\displaystyle \mathrm { Q }$는 어느 점으로 한없이 가까이 가는가?

 

 

 

 

 

27. 두 곡선 $\displaystyle y=\ln \left ( 2x+1 \right ) $, $\displaystyle y=-\ln x ^ {3} +k $가 서로 직교하도록 하는 상수 $\displaystyle k $의 값을 구하여라.

 

 

 

 

28. 실수 전체의 집합에서 정의된 미분가능한 함수 $\displaystyle f ( x) $가 $\displaystyle a < b < c $인 모든 $\displaystyle a,~b,~c $에 대하여

$$\displaystyle \frac {f ( b)-f ( a)} {b-a} < \frac {f ( c)-f ( b)} {c-b} $$

일 필요충분조건은 $\displaystyle x _ {1} < x _ {2} $인 모든 $\displaystyle x _ {1} ,~x _ {2} $에 대하여 $\displaystyle f ' ( x _ {1} ) < f ' ( x _ {2} ) $임을 증명하여라. [94 서울대]

 

 

 

29. 평균값의 정리를 이용하여 $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {\sin x-\sin \left ( \sin x \right )} {x-\sin x} } $의 값을 구하여라.

 

 

 

 

 

30. 함수 $\displaystyle f ( x)=e ^ {-x} \sin x $ ($\displaystyle x>0 $)에 대하여 곡선 $\displaystyle y=f ( x) $의 $\displaystyle x $절편을 작은 것부터 차례로 $\displaystyle x _ {1} ,~x _ {2} ,~ \cdots ,~x _ {n} ,~ \cdots $이라고 하자. 점 $\displaystyle \left ( x _ {n} ,~0 \right ) $에서 이 곡선에 접하는 직선의 $\displaystyle y $절편을 $\displaystyle y _ {n} $이라고 할 때, $\displaystyle \sum\limits _ {n=1} ^ {\infty } \frac {y _ {n} } {n} $의 값을 구하여라.

 

 

 

 

31. $\displaystyle f ( 0)=0 $이고, $\displaystyle f ' ( x) $가 증가함수이면 $\displaystyle x>0 $일 때, $\displaystyle \frac {f ( x)} {x} $가 증가함수임을 보여라. 단, 어떤 함수 $\displaystyle g ( x) $가 증가함수라는 것은 $\displaystyle x _ {1} < x _ {2} $이면 $\displaystyle g ( x _ {1} ) < g ( x _ {2} ) $임을 의미한다.

 

 

 

 

 

32. $\displaystyle x>0 $에서 정의된 함수 $\displaystyle f ( x) $는 다음 두가지 조건을 만족한다.

(i) $\displaystyle f ( x) $는 $\displaystyle x>0 $에서 2번 미분가능하고 $\displaystyle f ( 1)=0,~f ' ( 1)=2 $

(ii) $\displaystyle x>0,~y>0 $인 모든 $\displaystyle x,~y $에 대하여 $\displaystyle f ( xy)=yf ( x)+xf ( y) $

이 때, $\displaystyle f '' ( x) $를 구하여라.

 

 

 

 

33. $$\displaystyle f ( x)= { \begin {cases} g ( x)\sin \frac {1} {x} ~ & ( x \neq 0)\\~0 & \left ( x=0 \right )\end {cases} } $$

이고 $\displaystyle g ( 0)=g ' ( 0)=0 $일 때, $\displaystyle f ' ( 0) $을 구하여라.

 

 

 

 

34. 모든 실수에서 정의된 함수 $\displaystyle f ( x) $가 다음 두 가지 조건을 만족한다.

---

(i) 임의의 실수 $\displaystyle x,~y $에 대하여 $\displaystyle 1+f ( x)f ( y) \neq 0 $이고,

$$\displaystyle f ( x+y)= \frac {f ( x)+f ( y)} {1+f ( x)f ( y)} $$

(ii) $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {f ( x)} {x} =1} $

---

(1) 모든 실수 $\displaystyle x $에 대하여 $\displaystyle f ' ( x) $가 존재함을 증명하여라.

(2) $\displaystyle f ( x) $가 증가함수임을 증명하여라. 단, $\displaystyle f ( x) $가 증가함수라 함은 $\displaystyle x _ {1} < x _ {2} $인 모든 $\displaystyle x _ {1} ,~x _ {2} $에 대하여 $\displaystyle f ( x _ {1} ) < f ( x _ {2} ) $가 성립함을 의미한다.

 

풀이 및 정답

(1) $\displaystyle \lim\limits _ {x \rightarrow 0} { \frac {f ( x)} {x} =1} $에서 \(\displaystyle \lim\limits _ {x \rightarrow 0}  {f ( x)}   =0 \)

또 $\displaystyle f ( x+y)= \frac {f ( x)+f ( y)} {1+f ( x)f ( y)} ~~\cdots\cdots ~(\mathrm{i})$을 이용하여 도함수 \(\displaystyle f'(x)\)를 구해보자.

\(\displaystyle \begin{align}f'(x)&=\lim\limits_{h \rightarrow 0}\frac{f(x+h)-f(x)}{h}\\&=\lim\limits_{h \rightarrow 0}\frac{1}{h} \left\{\frac{f(x)+f(h)}{1+f(x)f(h)}-f(x) \right\}\\&=\lim\limits_{h \rightarrow 0}  \frac{f(h)}{h}\frac{  \left[1-\left\{f(x)\right\}^2  \right]}{  \left\{1+f(x)f(h)\right\}} \\&=1\times \left[ 1-\left\{f(x)\right\}^2   \right]\\& =1-\left\{f(x)\right\}^2    \end{align}\)

즉 \(\displaystyle f'(x) =1-\left\{f(x)\right\}^2    \)

따라서 \(\displaystyle f(x)\)는 모든 실수 \(\displaystyle x\)에 대해 \(\displaystyle f'(x)\)가 존재한다.

 

(2) \(\displaystyle (\mathrm{i})\)에서 \(\displaystyle x=y=0\)을 대입하면

$\displaystyle f ( 0+0)= \frac {f ( 0)+f ( 0)} {1+f (0)f (0)} $

\(\displaystyle f ( 0)\left[1+\left\{f(0)\right\}^2 \right]=2f(0)\)

\(\displaystyle f ( 0)\left[-1+\left\{f(0)\right\}^2 \right]=0\)

\(\displaystyle \therefore~f ( 0)=0 ~또는~\pm1\)

첫째 \(\displaystyle f ( 0)=1\)일 때, \(\displaystyle (\mathrm{i})\)의 \(\displaystyle y\)에 \(\displaystyle 0\)을 대입하면 

$$\displaystyle \begin{align}f ( x+0)&= \frac {f ( x)+f ( 0)} {1+f ( x)f ( 0)}\\&=\frac {f ( x)+1} {1+f ( x)}=1 \end{align} $$

이것은 조건 \(\displaystyle (\mathrm{ii})\)와 모순이다. 분모는 \(\displaystyle 0\)으로 분자는 \(\displaystyle 1\)로 가기 때문에 극한값이 \(\displaystyle 1\)인 것과 모순이다.

둘째 \(\displaystyle f ( 0)=-1\)일 때, \(\displaystyle (\mathrm{i})\)의 \(\displaystyle y\)에 \(\displaystyle 0\)을 대입하면

$$\displaystyle \begin{align}f ( x+0)&= \frac {f ( x)+f ( 0)} {1+f ( x)f ( 0)}\\&=\frac {f ( x)-1} {1-f ( x)}=-1 \end{align} $$

이것 역시 조건 \(\displaystyle (\mathrm{ii})\)와 모순이다. 분모는 \(\displaystyle 0\)으로 분자는 \(\displaystyle -1\)로 가기 때문에 극한값이 \(\displaystyle 1\)인 것과 모순이다.

따라서 \(\displaystyle  f ( 0)=0  \)

또, 조건 \(\displaystyle (\mathrm{i})\)에서 \(\displaystyle y\)대신 \(\displaystyle -x \)를 대입하면

$$\displaystyle \begin{align}0=f(0)&=f ( x+(\textcolor{red}{-x}))\\&= \frac {f ( x)+f ( -x)} {1+f ( x)f ( -x)} \end{align} $$

조건 $\displaystyle 1+f ( x)f ( y) \neq 0 $에서 분모는 \(\displaystyle 0\)이 아니므로

\(\displaystyle f(-x)=-f(x)\)

즉, 원점에 대칭인 함수이다.

다음을 보이자.

모든  실수 \(\displaystyle x\)에 대하여 \(\displaystyle f(x) \neq \pm1\)임이다.

왜냐하면 \(\displaystyle f(x_0 )=1\)인 \(\displaystyle x_0\)가 존재하다고 하면

$$\displaystyle \begin{align} f(x) &=f(x-x_0 +x_0 )\\&= \frac {f ( x-x_0)+f ( x_0)} {1+f ( x-x_0)f ( x_0)}\\&=  \frac {f ( x-x_0)+1} {1+f ( x-x_0)}=1 \end{align} $$

즉 모든 실수  \(\displaystyle x\)에 대하여  \(\displaystyle f(x)=1\)이므로 조건  \(\displaystyle ( \mathrm{ii})\)과 모순이다.

또,  \(\displaystyle f(x)\)는 기함수이므로  \(\displaystyle f(x) \neq -1\)이다.

이제 \(\displaystyle -1 < f(x) < 1\)임을 보이면  \(\displaystyle f'(x) =1-\left\{f(x)\right\}^2    \)에서  \(\displaystyle f'(x) >0    \)이므로  \(\displaystyle f(x)\)는 증가함수임을 보일 수 있다.

귀류법으로 보이자.  \(\displaystyle f(0) =0   \)이므로 어떤 실수  \(\displaystyle \alpha\)가 존재하여  \(\displaystyle f(\alpha)>1  \)라고 가정하자. 

함수  \(\displaystyle f(x)\)는 모든 실수  \(\displaystyle x\)에 대하여 도함수가 존재하므로 연속함수이다. 또,  \(\displaystyle f(0)=0,~f(\alpha)>1\)이므로 사잇값의 정리에 의해  \(\displaystyle f(c)=1\)인  \(\displaystyle c\)가 존재한다. 이것은 모든 실수  \(\displaystyle x\)에 대하여  \(\displaystyle f(x) \neq \pm1\)이라는 사실과 모순이다.

또, 기함수이므로  \(\displaystyle f(x) < -1\)인  \(\displaystyle x\)값도 존재하지 않는다. 즉,  

\(\displaystyle -1<f(x)<1\)

따라서 \(\displaystyle f'(x) =1-\left\{f(x)\right\}^2    \)에서 \(\displaystyle f'(x)>0\), 즉 \(\displaystyle f(x)\)는 증가함수이다.

ㅠㅠ