[수학의 기초] 파푸스-귤단의 원리(1)-질량중심에 대하여 [더플러스수학학원]

울산과고2학년 심화수학2 과목에서 회전체의 부피 구하는 과정에서 파푸스-귤딘의 원리를 이용하서 푸는 문제가 나와서 학생들이 파푸스-귤딘의 원리에 대해 대략적으로 알 수 있지만 구체적으로 무엇을 의미하는지 잘 몰라 울산과고전문 더플러스수학학원에서 이를 위해 먼저  질량중심에 대해서 설명하고 이후 2편에서 파푸스-귤단의 원리에 대해 정리하겠다.
이 글은 다음을 목표로 한다.

학습 교안: 파푸스의 귤단의 원리를 이용한 회전체의 부피 계산

학습 교안: 파푸스의 귤단의 원리를 이용한 회전체의 부피 계산

목표
- 파푸스의 귤단의 원리에 대해 이해한다.
- 질량 중심의 개념을 이해하고 회전체의 부피를 계산할 때 그 중요성을 인식한다.
- 파푸스의 귤단의 원리를 사용하여 다양한 도형의 회전체 부피를 계산할 수 있다.

먼저 파푸스 귤단의 원리에 대해 먼저 적어보면 다음과 같다.

파푸스-귤딘의 원리

파푸스의 귤단의 원리는 기하학적 도형이 회전할 때 생성되는 회전체의 부피(표면적은 다음 기회로 미루자)을 계산하는 데 사용되는 수학적 정리이다. 이 원리는 기본적으로 두 가지 중요한 정리로 나누는데 여기서는 회전체의 부피를 계산하는 데 집중하여 파푸스의 첫 번째 귤단의 원리를 설명하겠습니다.

이 원리는 평면 도형이 고정된 축 주위를 회전하여 생성되는 회전체의 부피를 계산하는 방법에 관한 것입니다. 원리에 따르면, 회전체의 부피는 회전하는 도형의 넓이와 그 도형의 질량 중심이 회전축 주위를 따라 이동한 거리(회전 반경)의 곱에 \(2\pi\)를 곱한 것과 같습니다.

공식     \(V = 2\pi R A \)
- \(V\)는 회전체의 부피입니다.
- \(R\)은 도형의 질량 중심에서 회전축까지의 거리(회전 반경)입니다.
- \(A\)는 회전하기 전 도형의 면적입니다.

부피 계산 방법

1. 도형 선택과 질량 중심 결정: 회전시킬 도형을 선택하고, 해당 도형의 질량 중심을 결정합니다.

2. 회전 반지름 결정: 도형의 질량 중심에서 회전축까지의 거리를 결정합니다. 이 거리는 회전 반경 \(R\)이 됩니다.

3. 도형의 넓이 계산: 회전하기 전 도형의 넓이 \(A\)를 계산합니다.

4. 부피 계산: 위에서 결정한 \(R\)과 \(A\)를 파푸스의 첫 번째 귤단의 원리 공식에 대입하여 회전체의 부피 \(V\)를 계산합니다.
파푸스의 귤단의 원리를 사용하면 복잡한 형태의 회전체도 간단히 부피를 계산할 수 있으며, 이 원리는 수학, 물리학, 공학 등 다양한 분야에서 유용하게 활용됩니다.
위의 과정을 위해 제일 중요한 개념은 질량중심이란 것을 이해하는 것이다.

질량 중심이란 무엇인가?

공학이 아닌 수학에서는, 또 고등학교 수학에서는 밀도가 일정한 경우라고 가정해도 된다.
물체의 밀도가 일정한 평면 도형의 경우, 질량 중심(또는 무게 중심)은 도형 내 모든 점의 평균 위치를 나타내며, 도형의 기하학적 중심과 일치합니다. 이런 경우, 질량 중심을 찾는 것은 도형의 대칭성과 기하학적 특성을 이용하여 상대적으로 간단합니다. 균일한 밀도를 가진 평면 도형의 질량 중심을 계산하는 공식은 도형의 형태에 따라 달라집니다.

평면 도형의 질량 중심 계산

평면 도형에서, 질량 중심은 다음과 같이 계산할 수 있습니다:

직사각형: 직사각형의 질량 중심은 그 중심에 위치합니다. 사각형이 $\displaystyle x$축과 $\displaystyle y$축에 평행하고, 가로 길이가 $\displaystyle b$, 세로 길이가 $\displaystyle h$일 경우, 질량 중심의 위치는 $\displaystyle \left(\frac{b}{2}, ~\frac{h}{2}\right)$입니다.
원: 원의 질량 중심은 원의 중심에 위치합니다. 즉, 원의 중심이 $\displaystyle (a, ~b)$일 경우, 질량 중심도 $\displaystyle (a, ~b)$에 위치합니다.

삼각형:일정한 밀도를 가진 삼각형의 질량 중심은 세 꼭짓점을 연결하는 중선의 교점(즉, 삼각형의 무게중심)에 위치한다. 즉, 세 꼭짓점의 좌표가 $\displaystyle (x_1,~ y_1)$, $\displaystyle (x_2,~ y_2)$, $\displaystyle (x_3, ~y_3)$일 때, 질량 중심은 $\displaystyle \left(\frac{x_1 + x_2 + x_3}{3}, ~\frac{y_1 + y_2 + y_3}{3}\right)$에 위치합니다.

연속체에 대한 적분 공식

균일한 밀도를 가진 연속적인 평면 도형의 경우, 질량 중심은 도형의 넓이에 대한 적분을 사용하여 계산할 수 있습니다:
-  \(x\)축에 대한 질량 중심 \(x_{\text{cm}}\) :
\[ x_{\text{cm}} = \frac{1}{A} \int x \, dA \]

-  \(y\)축에 대한 질량 중심 \(y_{\text{cm}}\) :
\[ y_{\text{cm}} = \frac{1}{A} \int y \, dA \]

여기서 \(A\)는 도형의 면적이며, \(dA\)는 도형의 미소 면적 요소이다. 이 공식들은 도형의 모든 부분이 일정한 밀도를 가지고 있을 때 적용된다. 넓이 \(A\)는 도형에 따라 다른 방식으로 계산할 수 있으며, 일반적으로는 적분을 사용하여 계산합니다.
그런데 위의 설명은 고등학교 학생들은 이해하기가 좀 힘들다. 이를 설명하기 위해 먼저 다음과 같은 그림을 고려하자.

위의 세 점 $x_1 ,~x_2 ,~x_3$과 각각의 질량 $m_1 ,~m_2 ,~m_3$에 대해 균형점 $\displaystyle \overline{x}$를 구하고자 한다. 중력가속도를 $g$라 할 때, 중력에 대해 힘이 균형을 이루기 위한 위치 $\overline{x}$를 구하자. 

$\displaystyle \left\{ (x_1 - \overline x )m_1 + (x_2 -\overline x )m_2 +(x_3 -\overline x)m_3 \right\} g =0$
$\displaystyle \therefore~ \overline x = \frac{m_1 x_1 +m_2 x_2 +m_3 x_3 }{m_1 +m _2 +m_3}$

이 때의 $\overline{x}$의 위치를 질량중심이라고 한다. 또, 이 위치는 세 점 $x_1 ,~x_2 ,~x_3$의 $m_1 ,~m_2 ,~m_3$에 대한 가중평균을 의미한다.
다른 관점으로 다시 해석하면
원점 $\mathrm O$(기준점)으로부터의 거리에 중력($m \times g$)를 곱한 값의 합을 원점에 대한 계의 모멘트(moment of the system about the origrin)이라 하고 그것은 개별 질량의 모멘트(moment) $m_1 x_1 +m_2 x_2 +m_3 x_3$의 합이다.
그리고 이것은 질량중심 $\overline{x}$에 질량의 합($m_1 +m_2 +m_3$)을 곱한 값의 합과 같다. 즉,

$\displaystyle m_1 x_1 +m_2 x_2 +m_3 x_3 = \overline{x}(m_1 +m_2 +m_3) $    $\cdots\cdots\cdots~ (\mathrm{i})$

즉, 질량중심은 

$\displaystyle  \overline{x}=\frac{ m_1 x_1 +m_2 x_2 +m_3 x_3  }{m_1 +m_2 +m_3} $

이것을 일반화하여 좌표평면에서 $(x_1 ,~y_1),~(x_2,~y_2 ),~(x_3,~y_3)$와  각각의 질량 $m_1 ,~m_2 ,~m_3$ 에 대하여 질량중심 $\displaystyle ( \overline x , ~\overline y)$ 을 구하면 

$\displaystyle\overline ( \overline x , ~\overline y) = \left(\frac{m_1 x_1 +m_2 x_2 +m_3 x_3 }{m_1 +m_2 +m_3},~ \frac{m_1 y_1 +m_2 y_2 +m_3 y_3 }{m_1 +m_2 +m_3} \right)$

이제 연속적인 변량에 대해 일차원, 즉 직선에서 질량중심을 구해보자. 우리는 밀도가 일정한 경우를 생각하므로 위에서의 질량은 그냥 넓이라고 해도 된다. 왜냐하면 넓이에 밀도를 곱하면 질량이 되고 계산을 다하면 결국 밀도는 소거가 되기 때문이다.

직사각형에서의 질량중심

구간 $[a,~b]$를 $n$등분하여 각각의 분점을 $a=x_0 ,~x_1 ,~\cdots,~x_{k-1},~x_k ,~\cdots,~x_n = b$라 하고 소구간 $[x_{k-1},~x_k]$에서 질량을 $\Delta m_k $라 하고, 그 구간의 중점  $c_k (x_{k-1} \leq c_k \leq x_k)$-소구간의 중점이 그 구간에서의 질량중심이다- 에 대하여

$\displaystyle \lim_{n \rightarrow \infty} \sum_{k=1}^n {(c_k -\overline{x})\Delta m_k }=0$
$\displaystyle \lim_{n \rightarrow \infty} \sum_{k=1}^n{ c_k  \Delta m_k }= \lim_{n \rightarrow \infty} \sum_{k=1}^n{ \overline{x} \Delta m_k } $

정적분의 정의에 의해

$\displaystyle \int_a^b x dm  = \int_a^b  { \overline{x} dm } $    $\displaystyle \int_a^b x dm  =\overline{x} \int_a^b  { dm } $
$\displaystyle \therefore~ \overline{x}=\frac{\displaystyle  \int_a^b x dm}{\displaystyle \int_a^b   dm } $

여기서 직사각형의 세로의 길이를 $w$라 하자. 또, 이 사각형의 밀도를 $\rho$라고 하면 $\Delta m_k = (x_k-x_{k-1})w \times \rho$이다. 즉 $dm = w \rho dx $
이를 위의 식에 대입하면

$\displaystyle \begin{aligned} \overline{x}& =\frac{\displaystyle  \int_a^b x dm}{\displaystyle \int_a^b   dm } = \frac{\displaystyle  \int_a^b x w \rho dx}{\displaystyle \int_a^b  w \rho dx } \\&=  \frac{\displaystyle w \rho \int_a^b x  dx}{\displaystyle w \rho \int_a^b    dx }  = \frac{\displaystyle \frac{b^2-a^2}{2}}{b-a}\\& = \frac{a+b}{2}\end{aligned}$

이 결과 밀도가 일정한 직사각형에서는 질량중심이 직사각형의 중점이 된다.
이제 연속적인 함수 $y=f(x)$ $(a \leq x \leq b)$에 대해 질량중심을 구해보자.  다음의 그림을 보자.

구간 $[a,~b]$를 $n$등분하여 각각의 분점을 $a=x_0 ,~x_1 ,~\cdots,~x_{k-1},~x_k ,~\cdots,~x_n = b$라 하고 소구간 $[x_{k-1},~x_k]$에 속하는 $c_k $에 대하여 질량중심 $( \overline{x},~ \overline{y})$를 구해보자. 여기서 밀도가 일정한 평면에서 질량중심을 구하기 때문에 넓이를 구해서 밀도를 곱할 필요없이 넓이만 구해도 된다.

$\displaystyle 0= \lim_{n \rightarrow \infty} \sum_{k=1}^n \left(c_k - \overline{x} \right) f(c_k ) (x_k -x_{k-1})$

정적분의 정의에 의해

$\displaystyle \int_a ^b (x -\overline{x})f(x)dx=0$          $\displaystyle \therefore ~ \overline{x} =\frac{\displaystyle \int_a^b x f(x)dx}{\displaystyle \int_a^b f(x)dx}$

 
이제 $\overline{y}$를 구해보자.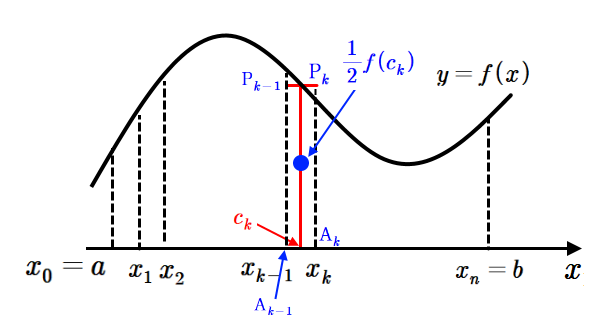 

 $(\mathrm{i})$에 의해 소구간 $[x_{k-1},~x_k]$에서 밑변의 길이 $x_k -x_{k-1}$, 높이를 $f(c_k )$로 하는 직사각형 $ \mathrm P_{k-1} \mathrm P_k \mathrm A_k \mathrm A_{k-1}$에서 질량중심은 $\displaystyle \frac{f(c_k)}{2}$이므로 이 질량중심에 직사각형의 넓이 $\displaystyle f(c_k )(x_k -x_{k-1})$를 곱하면

$\displaystyle \frac{f(c_k )}{2} f(c_k )(x_k -x_{k-1})$

이것을 모두 합하고 극한($\displaystyle lim_{n \rightarrow \infty}$)을 취하면 정적분의 정의에 의해 

$\displaystyle \lim_{n \rightarrow \infty} \sum_{k=1}^n \frac{f(c_k )}{2} f(c_k )(x_k -x_{k-1}) =\int_a^b \frac{\left\{f(x)\right\}^2}{2}dx$

이 값은 원점에 대한 계의 모멘트(moment of the system about the origrin)이다. 
그런데 이 값은 $y$축 방향의 질량중심 $\overline{y}$에 넓이 $\displaystyle \int_a^b f(x)dx$를 곱한 값과 서로 같다. 즉,

$\displaystyle \int_a^b \frac{\left\{f(x)\right\}^2}{2}dx = \overline{y} \int_a^b f(x)dx$
$\displaystyle \therefore~  \overline{y} = \frac{\displaystyle \frac{1}{2} \int_a^b  \left\{f(x)\right\}^2 dx }{  \displaystyle\int_a^b f(x)dx}$

 
예를 들어 보자. 아래 그림에서의 삼각형의 질량중심을 구해보자.

$f(x)=2x ~(0 \leq x \leq 1)$

먼저 질량중심의 $x$ 좌표 $\overline{x}$를 구해보면

$\displaystyle \begin{aligned} \overline{x}&= \frac{\displaystyle\int_0^1 xf(x)dx}{\displaystyle\int_0^1 f(x)dx} = \frac{\displaystyle\int_0^1 2x^2dx }{\displaystyle\int_0^1 2xdx}\\&=\frac{2}{3}\end{aligned} $

또, 질량중심의 $y$ 좌표 $\overline{y}$를 구해보면

$\displaystyle \begin{aligned}  \overline{y}&  = \frac{\displaystyle \frac{1}{2} \int_0^1  \left\{f(x)\right\}^2  dx }{  \displaystyle\int_0^1 f(x)dx} \\&  = \frac{\displaystyle \frac{1}{2} \int_0^1  \left\{2x\right\}^2  dx }{  \displaystyle\int_0^1 2xdx} \\&= \frac{2}{3} \end{aligned}$

따라서 질량중심의 좌표는 $\displaystyle \left(\frac{2}{3},~\frac{2}{3}\right)$
물론 위의처럼 $dx$를 사용하지 않고 $dy$를 사용하면 

$\displaystyle \begin{aligned}  \overline{y}&  = \frac{\displaystyle\int_0^2 y \left(1- \frac{1}{2}y \right)dy }{\displaystyle\int_0^1 2xdx} \\&=  \displaystyle  \int_0^2 y- \frac{y^2}{2} dy = \left[\frac{y^2}{2}  -\frac{y^3}{6} \right]_0^1     \\&= \frac{2}{3} \end{aligned}$