[수학의 기초] 파푸스-귤딘의 원리(2)-회전체의 부피 [더플러스수학학원]

울산과고2학년 심화수학2 과목에서 회전체의 부피 구하는 과정에서 파푸스-귤딘의 원리를 이용하서 푸는 문제가 나와서 학생들이 파푸스-귤딘의 원리에 대해 대략적으로 알 수 있지만 구체적으로 무엇을 의미하는지 잘 몰라 울산과고전문 더플러스수학학원에서 이를 위해 전편의 질량중심에 대한 설명 이후 이제 2편에서는 파푸스-귤딘의 정리에 대해 정리하겠다.
이 글은 다음을 목표로 한다.

학습 교안: 파푸스의 귤단의 원리를 이용한 회전체의 부피 계산

학습 교안: 파푸스의 귤단의 원리를 이용한 회전체의 부피 계산

목표
- 파푸스의 귤단의 원리에 대해 이해한다.
- 질량 중심의 개념을 이해하고 회전체의 부피를 계산할 때 그 중요성을 인식한다.
- 파푸스의 귤단의 원리를 사용하여 다양한 도형의 회전체 부피를 계산할 수 있다.

먼저 파푸스 귤단의 원리에 대해 먼저 적어보면 다음과 같다.

파푸스-귤딘의 원리

파푸스의 귤단의 원리는 기하학적 도형이 회전할 때 생성되는 회전체의 부피(표면적은 다음 기회로 미루자)을 계산하는 데 사용되는 수학적 정리이다. 이 원리는 기본적으로 두 가지 중요한 정리로 나누는데 여기서는 회전체의 부피를 계산하는 데 집중하여 파푸스의 첫 번째 귤단의 원리를 설명하겠습니다.

이 원리는 평면 도형이 고정된 축 주위를 회전하여 생성되는 회전체의 부피를 계산하는 방법에 관한 것입니다. 원리에 따르면, 회전체의 부피는 회전하는 도형의 넓이와 그 도형의 질량 중심이 회전축 주위를 따라 이동한 거리(회전 반경)의 곱에 \(2\pi\)를 곱한 것과 같습니다.

공식     \(V = 2\pi R A \)
- \(V\)는 회전체의 부피입니다.
- \(R\)은 도형의 질량 중심에서 회전축까지의 거리(회전 반경)입니다.
- \(A\)는 회전하기 전 도형의 면적입니다.

부피 계산 방법

1. 도형 선택과 질량 중심 결정: 회전시킬 도형을 선택하고, 해당 도형의 질량 중심을 결정합니다.

2. 회전 반지름 결정: 도형의 질량 중심에서 회전축까지의 거리를 결정합니다. 이 거리는 회전 반경 \(R\)이 됩니다.

3. 도형의 넓이 계산: 회전하기 전 도형의 넓이 \(A\)를 계산합니다.

4. 부피 계산: 위에서 결정한 \(R\)과 \(A\)를 파푸스의 첫 번째 귤단의 원리 공식에 대입하여 회전체의 부피 \(V\)를 계산합니다.
파푸스의 귤단의 원리를 사용하면 복잡한 형태의 회전체도 간단히 부피를 계산할 수 있으며, 이 원리는 수학, 물리학, 공학 등 다양한 분야에서 유용하게 활용됩니다.
위의 과정을 위해 제일 중요한 개념은 질량중심이란 것을 이해하는 것이다.

정리1. 부피에 대한 파푸스의 정리

평면영역을 그 영역의 내부와 만나지 않는 그 평면 위의 한 직선 둘레로 회전하여 생기는 입체의 부피는 영역의 넓이와 그 영역의 질량중심이 회전할 때 움직인 거리의 곱이다. 만일 $\displaystyle \rho$가 회전축과 질량 중심사이의 거리라 하면 $$ V= 2 \pi \rho A$$

 
(증명) 평면영역을 적절히 회전이동, 평행이동하여 회전축을 $x$축이 되도록 옮기고 평면영역의 경계를 $y=f(x),~y=g(x) ~(f(x) \geq g(x))$ ($a \leq x \leq b)$라 하자.
먼저 Disk Method로, 즉, 미적분의 회전체의 부피구하는 방법으로 부피를 구하면

$\displaystyle  V= \int_a^b \left\{f(x) \right\}^2 - \left\{g(x)\right\}^2 dx$   $\cdots\cdots ①$

또, 구간 $[a,~b]$에서 $f(x),~g(x)$로 둘러싸인 부분의 $y$축 방향의 질량중심 $\overline{y}$는 (질량중심 공식에 대해서는 전편을 찾아보세요.)

$\displaystyle  \overline{y} = \frac{\displaystyle\frac{1}{2} \int_a^b \left\{f(x) \right\}^2 - \left\{g(x)\right\}^2 dx}{\displaystyle \int_a^b f(x)-g(x)dx}$

이다. 따라서 파푸스-귤단의 정리에 의해

$\displaystyle \begin{aligned}  V & = 2\pi \overline{y} \int_a^b f(x)-g(x)dx\\& = 2\pi  \frac{\displaystyle\frac{1}{2}\displaystyle \int_a^b \left\{f(x) \right\}^2 - \left\{g(x)\right\}^2 dx}{\displaystyle \int_a^b f(x)-g(x)dx}  \times \displaystyle \int_a^b f(x)-g(x)dx\\&=\pi \int_a^b \left\{f(x) \right\}^2 - \left\{g(x)\right\}^2 dx  ~~~\cdots\cdots ~②  \end{aligned}$

①, ②에서 증명되었다.

 

정리2. 부피를 구하는 또다른 공식(Shell Method)-파푸스귤단의 정리

연속함수 $y=f(x) ~(a \leq x \leq b)$와 $x$축으로 둘러싸인 둘러싸인 부분을 $y$축의 둘레로 회전시킨 입체의 부피를 구하면 
                                              $\displaystyle V= 2\pi \int_a^b xf(x)dx$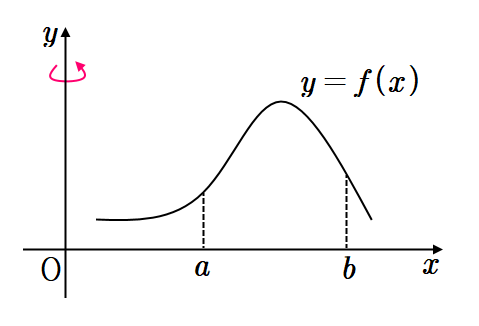

(증명) $y$축으로 회전한 입체의 부피를 파푸스귤단의 원리로 구하기 위해 먼저 $\overline{x}$를 구해보자. (질량중심 공식에 대해서는 전편을 찾아보세요.)

$\displaystyle \overline{x}=\frac{ \displaystyle \int_a^b x f(x)dx}{\displaystyle \int_a^b f(x)dx} $

따라서 파푸스 귤단의 원리에 의해 부피 $V$는

$\displaystyle \begin{aligned}  V &= 2\pi \overline{x} \times \int_a^b f(x)dx \\&=2 \pi  \frac{ \displaystyle \int_a^b x f(x)dx}{\displaystyle \int_a^b f(x)dx} \times \int_a^b f(x)dx \\&= 2\pi \int_a^b x f(x)dx \end{aligned}$