[수학의 기초] $y=f(x)$와 $y=mx+c$로 둘러싸인 넓이와 회전체의 부피 [더플러스수학학원]

울산옥동에 있는 울산과고전문 더플러스수학학원입니다. 울산과고2학년 심화수학1 수업, 미적분에서 $x,~y$축 둘레로 회전하는 회전체의 부피 구하는 방법을 조금 더 일반화라는  과제가 학생들에게 나왔다. 이제 울산과고 전문 더플러스수학학원에서는 새롭게 정적분의 정의로 구해 봤다. 곡선 $y=f(x)$와 직선 $y=mx+c$로 둘러싸인 부분의 부피를 구해보자. 또, 비슷한 방법으로  곡선 $y=f(x)$ 와 직선 $y=mx+c$로 둘러싸인 부분의 넓이를 구하자.

https://youtu.be/73JXOCUs2jU
 

 

$y=f(x)$와 $y=mx+c$로 둘러싸인 부분의 회전체의 부피

먼저 다음 그림과 같은 고려해 보자.

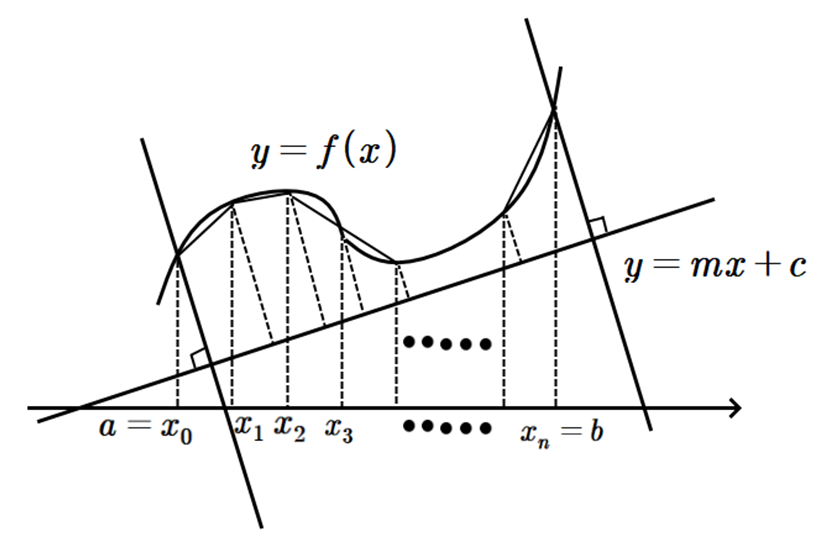
이 닫힌구간 \(\displaystyle [a,~b] \)에서 연속 함수 \(\displaystyle y=f ( x) \)와 직선 \(\displaystyle y=mx+c \) (\(\displaystyle m \neq 0 \))가 주어질 때, 곡선 \(\displaystyle y=f ( x) \)와 세 직선 \(\displaystyle y=mx+c \), \(\displaystyle y=- \frac {1} {m} ( x-a)+f ( a),~y=- \frac {1} {m} ( x-b)+f ( b) \)로 둘러싸인 부분을 직선 \(\displaystyle y=mx+c \)의 둘레로 회전한 입체의 부피를 구하면 다음과 같다.

\(\displaystyle V= \frac {\pi } { ( 1+m ^ {2} ) \sqrt {1+m ^ {2} } } \int _ {a} ^ {b} {\left\{ f ( x)-mx-c \right\} ^ {2} \left | 1+mf ' ( x) \right | dx} \)

(증명) 닫힌구간 \(\displaystyle [a,~b] \)를 균등분할하여 \(\displaystyle a=x _ {0} ,~x _ {1} ,~x _ {2} ,~ \cdots ,~x _ {k-1} ,~x _ {k} ,~ \cdots ,~x _ {n} =b \)라 하자.

\(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k} ,~f ( x _ {k} )) \)을 지나며 직선 \(\displaystyle y=mx+c \)에 수직인 직선을 구하면

\(\displaystyle y=- \frac {1} {m} ( x-x _ {k} )+f ( x _ {k} ) \)
\(\displaystyle x+my-mf ( x _ {k} )-x _ {k} =0 \) \(\displaystyle \cdots \cdots \)①

\(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k-1} ,~f ( x _ {k-1} )) \)에서 직선 ①까지의 거리 \(\displaystyle \Delta u \)는

\(\displaystyle \frac {\left | x _ {k-1} +mf \left ( x _ {k-1} \right ) -mf ( x _ {k} )-x _ {k} \right |} {\sqrt {1+m ^ {2} } } \)
\(\displaystyle \left . \frac {\left | ( x _ {k} -x _ {k-1} )+m \left\{ f \left ( x _ {k} \right ) -f ( x _ {k-1} ) \right\} \right |} {\sqrt {1+m ^ {2} } } \right . \)

평균값의 정리를 적용하면

\(\displaystyle \left . \frac {\left | 1+mf ' ( c _ {k} ) \right |} {\sqrt {1+m ^ {2} } } \right . ( x _ {k} -x _ {k-1} ) \) \(\displaystyle ( x _ {k-1} <c _ {k} <x _ {k} ) \)

또, \(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k} ,~f ( x _ {k} )) \)에서 \(\displaystyle y=mx+c \), \(\displaystyle mx-y+c=0 \) 사이의 거리를 구하면 이것이 회전체의 반지름이다. 따라서

\(\displaystyle \frac {\left | mx _ {k} -f ( x _ {k} )+c \right |} {\sqrt {1+m ^ {2} } } \)

따라서 구간 \(\displaystyle [x _ {k-1} ,~x _ {k} ] \)에서 \(\displaystyle y=f ( x) \)와 \(\displaystyle y=mx+c \)로 둘러싸인 부분을 \(\displaystyle y=mx+c \) 둘레로 회전한 입체의 부피 \(\displaystyle \Delta V _ {k} \)는

\(\displaystyle \Delta  V _ {k} = \pi \left\{ \frac {\left | mx _ {k} -f ( x _ {k} )+c \right |} {\sqrt {1+m ^ {2} } } \right\} ^ {2} \left . \frac {\left | 1+mf ' ( c _ {k} ) \right |} {\sqrt {1+m ^ {2} } } \right . ( x _ {k} -x _ {k-1} ) \)

따라서 회전체의 부피 \(\displaystyle V \)는 정적분의 정의에 의해

\(\displaystyle \begin{aligned}  V & = \lim\limits _ {n \rightarrow \infty }   \sum\limits _ {k=1} ^ {n} \Delta  V _ {k} \\&=\pi \lim\limits _ {n \rightarrow \infty }   \sum\limits _ {k=1} ^ {n}   \frac {\left | m x _ {k} - f ( x _ {k} )+c \right |} {\sqrt {1+m ^ {2} } }   ^ {2}   \frac {\left | 1+mf ' ( c _ {k} ) \right |} {\sqrt {1+m ^ {2} } }   ( x _ {k} -x _ {k-1} ) \\& =\pi \int _ { a} ^ {b }   \frac { ( mx -f ( x)+c)^2 |1+mf' ( x)|} { ( 1+m^2 ) \sqrt {1+m^2} } dx \end{aligned}\)

 

$y=f(x)$와 $y=mx+c$로 둘러싸인 부분의 넓이

이번엔 둘러싸인 부분의 넓이 \(\displaystyle S \)를 구해보자.

(증명) 닫힌구간 \(\displaystyle [a,b] \)를 균등분할하여 \(\displaystyle a=x _ {0} ,~x _ {1} ,~x _ {2} ,~ \cdots ,~x _ {k-1} ,~x _ {k} ,~ \cdots ,~x _ {n} =b \)라 하자.
\(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k} ,~f ( x _ {k} )) \)을 지나며 직선 \(\displaystyle y=mx+c \)에 수직인 직선을 구하면 \(\displaystyle y=- \frac {1} {m} ( x-x _ {k} )+f ( x _ {k} ) \)

\(\displaystyle x+my-mf ( x _ {k} )-x _ {k} =0 \) \(\displaystyle \cdots \cdots \)①

\(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k-1} ,~f ( x _ {k-1} )) \)에서 직선 ①까지의 거리 \(\displaystyle \Delta  u \)는

\(\displaystyle \frac {\left | x _ {k-1} +mf \left ( x _ {k-1} \right ) -mf ( x _ {k} )-x _ {k} \right |} {\sqrt {1+m ^ {2} } } \)
\(\displaystyle \left . \frac {\left | ( x _ {k} -x _ {k-1} )+m \left\{ f \left ( x _ {k} \right ) -f ( x _ {k-1} ) \right\} \right |} {\sqrt {1+m ^ {2} } } \right . \)

평균값의 정리를 적용하면

\(\displaystyle \left . \frac {\left | 1+mf ' ( c _ {k} ) \right |} {\sqrt {1+m ^ {2} } } \right . ( x _ {k} -x _ {k-1} ) \) \(\displaystyle ( x _ {k-1} <c _ {k} <x _ {k} ) \)

또, \(\displaystyle y=f ( x) \) 위의 점 \(\displaystyle ( x _ {k} ,~f ( x _ {k} )) \)에서 \(\displaystyle y=mx+c \), \(\displaystyle mx-y+c=0 \) 사이의 거리를 구하면 이것이 구하고자 넓이의 높이이다. 따라서

\(\displaystyle \frac {\left | mx _ {k} -f \left ( x _ {k} \right ) +c \right |} {\sqrt {1+m ^ {2} } } \)

따라서 구간 \(\displaystyle [x _ {k-1} ,~x _ {k} ] \)에서 \(\displaystyle y=f ( x) \)와 \(\displaystyle y=mx+c \)로 둘러싸인 부분의 넓이는 \(\displaystyle \Delta S _ {k} \)는

\(\displaystyle \Delta  S _ {k} = \frac {\left | mx _ {k} -f ( x _ {k} )+c \right |} {\sqrt {1+m ^ {2} } } \left . \frac {\left | 1+mf ' ( c _ {k} ) \right |} {\sqrt {1+m ^ {2} } } \right . ( x _ {k} -x _ {k-1} ) \)

따라서 넓이 \(\displaystyle S \)는 정적분의 정의에 의해

\(\displaystyle\begin{aligned} S & = \lim\limits _ {n \rightarrow \infty }   \sum\limits _ {k=1} ^ {n} \Delta  S _ {k} \\& = \lim\limits _ {n \rightarrow \infty }   \sum\limits _ {k=1} ^ {n} \frac {\left | mx _ {k} - f ( x _ {k} )+c \right |\left | 1+mf ' ( c _ {k} ) \right |} {1+m ^ {2} } ( x _ {k} -x _ {k-1} )\\&  = \int _ {a} ^ {b} { \frac {\left | mx-f ( x)+c \right | \vert 1+mf ' ( x)\vert } {   1+m ^ {2}  } dx} \end{aligned}\)