[시험대비] 2019과고 1학년 2학기 기말고사대비문제(미적분,수1)

 

1. 다음 식의 값을 구하여라.[2.5점]

$$ \cos ^ {2} \theta +\cos ^ {2} \left ( \theta + \frac {\pi } {3} \right ) -\cos \theta \cos \left ( \theta + \frac {\pi } {3} \right ) $$

[2011 과고1 심화수학 2학기 중간7]

 

 

2. $ x $의 방정식 $ 25x ^ {2} -ax+12=0 $의 두 근이 $ \sin 2 \theta ,~\cos 2 \theta $일 때, $ \tan \theta $의 값의 합을 구하여라.[2.5점]

[2011 과고1 심화수학 2학기 중간8]

 

 

3. $ \alpha ,~ \beta $가 $ \tan \alpha -\tan \beta =1 $을 만족시킨다. $ \alpha $가 $ 0 \leq \alpha \leq \frac {\pi } {4} $의 범위에서 $ \tan ( \alpha - \beta ) $의 최댓값을 $ \mathrm M $, 최솟값을 $ m $이라 할 때, $ \mathrm M+m $의 값을 구하여라.[2.5점]

[2011 과고1 심화수학 2학기 중간9]

 

 

4. $ \theta =4 ^{\circ } $일 때, $ \mathrm P=2\sin \theta ( \cos \theta +\cos 3 \theta +\cos 5 \theta + \cdots +\cos 59 \theta ) $의 값을 구여라.[3.3점]

[2011 과고1 심화수학 2학기 중간11]

 

 

5. 그림과 같이 $ \mathrm {\angle BAC}=90 ^{\circ } $인 직각이등변삼각형 $ \mathrm {ABC} $가 반지름의 길이가 $ 1 $인 원 $ \mathrm O $에 내접하고 있다. 호$ \mathrm AC $ 위에서 움직이는 점 $ \mathrm P $에 대하여 $ \mathrm {\angle POA}= \alpha $($ 0 ^{\circ } < \alpha <90 ^{\circ } $)라 할 때, $ \mathrm { \overline {PA} + \overline {PB} + \overline {PC} }$의 최댓값을 구하여라. [3.4점]

[2011 과고1 심화수학 2학기 중간10]

 

6. 실수 $ b,~c $와 $ 0 \leq x \leq \pi $에 대하여 정의된 함수 $ f ( x)=a\sin ^ {2} x+b\cos ^ {2} x+c\sin x\cos x $의 최댓값이 $ 2 $, 최솟값이 $ -1 $이라고 한다. 이 때, 정수 $ a $의 개수를 구하여라. [3.4점]

[2011 과고1 심화수학 2학기 중간12]

 

 

 

 

7. $ 0 \leq x< \pi $에서 방정식 $ \tan x\tan 5x=1 $의 가장 작은 근을 $ \alpha $, 가장 큰근을 $ \beta $라 할 때, $ \beta - \alpha $의 값을 구하여라. [2.8점]

[2013 과고1 2학기 중간 18]

 

 

 

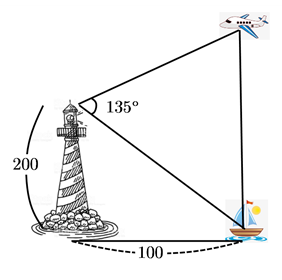
8. [서술형3] 그림과 같이 등대에서 배를 바라보는 시선과 배위의 수직으로 떠있는 비행기를 바라보는 시선이 이루는 각의 크기가 $ 135 ^{\circ } $이며, 해수면에서 등대까지의 높이가 $ 200 $, 등대에서 해수면에 내린 수선에서 배까지의 거리가 $ 100 $이다. 이 때, 배에서 비행기까지의 높이를 구하시오.(단, 비행기와 배의 크기는 무시한다.)

[2011 과고1 심화수학 2학기 중간 서술3]

 

 

 

9. $ \mathrm {\overline {AB} = \overline {AC}} $인 이등변삼각형 $ \mathrm ABC $에서 $ \mathrm {\angle A}=120 ^{\circ } $, $ \mathrm {\overline {BC} }=4 $이고 변 $ \mathrm {\overline {AC} }$ 위를 움직이는 점을 $ \mathrm P $라고 하면 $ \mathrm {\overline {BP} ^ {2} + \overline {CP} ^ {2}} $의 최솟값을 구하여라.[2.8점]

[2013 과고1 2학기 중간 13]

 

 

10. 그림과 같이 $ \mathrm {\overline {BC}} =2 $, $ \mathrm {\angle BAC=90} ^{\circ } $인 직각삼각형 $ \mathrm {ABC} $에서 선분 $ \mathrm {BC} $의 연장선 위에 $ \mathrm {\angle ABC= \angle CAD= \theta }$가 되도록 점 $ \mathrm D $를 잡는다. $ \theta =22.5° $일 때, 선분 $ \mathrm {AD} $의 길이를 구하여라. [2.7점]

[2013 과고1 2학기 중간 17]

 

 

10. $ \mathrm {\triangle ABC} $에서 $ \mathrm{ \overline {AB}} = a $ ($ a $는 상수), $ \angle \mathrm {BCA}= \theta $, $ \angle \mathrm {ABC=2 \angle BCA }$일 때, $ \lim\limits _ {\theta \rightarrow 0} { \frac {\mathrm{ \overline {AB} - \overline {BC} + \overline {CA} } } {\theta ^ {2} } } $의 값의 값을 구하여라. [3점]

[2013 과고1 2학기 중간 19]

 

 

 

11. 넓이가 $ \mathrm S $인 정$ n $각형($ n \geq 3 $)의 둘레의 길이를 $ l ( n) $이라 할 때, $ \lim\limits _ {n \rightarrow \infty } {l ( n)} $의 값을 구하여라. [3.1점]

[2013 과고1 2 기 중간 22]

 

 

 

12. 함수 $ f ( x)=\ln ( x ^ {2} +ax+b) $는 점 $ ( 2,~\ln 2) $에서 변곡점을 갖고, 점 $ ( 2,~\ln 2) $에서의 이 곡선의 접선의 기울기가 양일 때, $ -ab $의 값을 구하여라.[2.9점]

[2015 과고2 1학기 기말 3]

 

 

 

13. 그림과 같이 $ x=k $가 두 함수 $ y=\ln ( x-1) $, $ y=\sin \frac {\pi } {2} x $의 그래프 및 $ x $축과 만나는 점을 각각 $ \mathrm {P,~Q,~R} $라 하자. 점 $ \mathrm A ( 2,~0) $에 대하여 $ \mathrm {\angle PAQ}= \theta $라 할 때, $ \lim\limits _ {k \rightarrow 2+} {\tan \theta } $의 값을 구하여라. [2.9점]

[2013 과고1 2 기 중간 23]

 

 

14. 이계도함수가 존재하는 함수 $ f ( x) $에 대하여 $ f '' ( x)>0 $, $ f ( 0)=1 $, $ f ( 1)=0 $일 때, $ f ' ( 0),~-1,~f ' ( 1) $을 큰 것부터 차례로 나열한 것은?[2.7점]

[2015 과고2 1학기 기말 7]

① $ -1,~f ' ( 0),~f ' ( 1) $

② $ f ' ( 0),~f ' ( 1),~-1 $

③ $ f ' ( 0),~-1,~~f ' ( 1) $

③ $ f ' ( 1),~f ' ( 0),~-1 $

⑤ $ f ' ( 1),~-1,~f ' ( 0) $

 

 

 

 

15. 구간 $ [1,~10] $에 속하는 임의의 두 실수 $ a,~b $($ a<b $)에 대하여 $$ \frac {\ln b-\ln a} {b-a} =k $$를 만족하는 실수 $ k $의 값의 범위를 구하시오.[3점]

[2015 과고2 1학기 기말 서술형1]

 

 

 

16. $ x $의 두 방정식 $ \ln x=kx $와 $ e ^ {x} =kx $가 모두 실근을 갖지 않을 때, $ k $의 값의 범위를 구하시오.[4점]

[2015 과고2 1학기 기말 서술형2]

 

 

17. 4.  $ f ( x) $가 닫힌 구간 $ [a,~b] $에서 $ f ' ( x),~f '' ( x) $가 존재할 때, 열린구간 $ ( a,~b) $ 내의 어떤 점 $ c $에 대하여 $$ f ( b)=f ( a)+f ' ( a) ( b-a)+ \frac {1} {2} f '' ( c) ( b-a) ^ {2} $$임을 증명하려고 한다. (A), (B), (C), (D), (E), (F) 각각에 알맞은 식을 완성하여라.[4점]

[2017 과고1 미적분II 2학기 기말 서술5]

---

$ g ( x)=  f ( b)- \left\{ f ( x)+f ' ( x) ( b-x)+k ( b-x) ^ {2} \right\} $라고 두자. 여기서 $k$는 $ g ( a)=0 $이 되도록 정한 상수이다.

그러면 $ g ( x) $는 롤의 정리를 만족시킨다.

왜냐하면 $ \underline { ( A)} ,~ \underline { (B)} ,~ \underline { (C)} $이기 때문이다. 따라서 $ ( a,~b) $ 내의 어떤 $ c $에 대하여 $ g ' ( c)=0 $이다.

그런데 $ g ' ( c)= \underline { ( D)} $이므로 $ k= \underline { ( E)} $이다.

그러면 $ 0=g ( a)= \underline { ( F)} $이고 이것을 정리하면 구하는 결과를 얻는다.

---

 

 

 

18. $ \frac {\pi } {2} \leq x \leq \pi $에서 함수 $ f ( x)=\sin ^ {2} x+2\sin x\cos x+3\cos ^ {2} x $는 $ x= \alpha $에서 최댓값을 갖고 $ x= \beta $에서 최솟값을 갖는다. 이 때, $ \frac {\alpha } {\beta } $의 값을 구하여라. [2.4점]

[2015 과고2 심화수학II 1학기 중간 13]

 

 

 

19. 두 점 ‘$ \mathrm {A,~B} $를 양 끝점으로 하는 반지름의 길이가 $ 1 $인 반원이 있다. 반원 위의 임의의 점 $ \mathrm P $에 대하여 $ \mathrm {6 \overline {AP} +8 \overline {BP}} $의 최댓값을 구하여라.[2.4점]

[2015 과고2 심화수학II 1학기 중간 14]

 

 

20. $ 0 \leq x \leq \pi $인 $ x $에 대하여 방정식 $ \log _ {2} |\sin x+\cos x|=a $의 실근의 개수가 가장 많이 존재하게 되는 상수 $ a $의 값을 구하여라.[3점]

[2015 과고2 심화수학II 1학기 중간 15]

 

 

 

21. $$ \lim\limits _ {n \rightarrow \infty } { \frac {1+2+3+ \cdots +n+n\sin n} {n ^ {2} -e ^ {-n} } } = \frac {b} {a} $$ (단, $ a,~b $는 서로소인 자연수)이다. $ ab $의 값을 구하여라.[2.6점]

[2015 과고2 심화수학II 1학기 중간 21]

 

 

 

22. 다항식 $ f ( x)f ' ( x)=f ( x)-f ' ( x)+2x ^ {3} -4x ^ {2} +6x-3 $이 성립할 때, $ f ( -1) $의 값을 구하여라.[3.4점]

[2015 과고2 심화수학II 1학기 중간 22]

 

 

23. 연속함수 $ f ( x) $가 $ \lim\limits _ {x \rightarrow 0} { \frac {a ^ {x} -1} {f ( x)-4} } =1 $를 만족한다. 곡선 $ y=f ( x) $ 위의 $ x=0 $인 점에서의 접선이 점 $ ( -1,~0) $을 지날 때, 양수 $ a $의 값을 구하여라.[3점]

[2015 과고2 심화수학II 1학기 중간 23]

 

 

24. 곡선 $ \sqrt {x} + \sqrt {y} = \sqrt {5} $ 위의 점 $ ( x,~y) $ (단, $ x \neq 0,~y \neq 0 $)에서의 접선이 $ x,~y $축과 만나는 점을 각각 $ \mathrm {P,~Q }$라 하고 원점을 $ \mathrm O $라 할 때, $ \mathrm {\overline {OP} + \overline {OQ}} $의 값을 구하여라.[2.6점]

[2015 과고2 심화수학II 1학기 중간 24]

 

 

25. 두 곡선 $ y=cx \sqrt {x} $ ($ c>0 $), $ y= \sqrt {x} $가 원점이 아닌 교점 $ \mathrm P $에서의 두 곡선의 접선이 이루는 각의 크기를 $ \theta $라 할 때, $ \tan \theta $의 최댓값을 구하여라.[4점]

[2015 과고2 심화수학II 1학기 중간 서술7]

 

 

26. $ f ( x)=\sin x-a\cos x-3x $가 감소함수일 때, 상수 $ a $가 취하는 범위는?[4.7점]

[2015 과고3 1학기 기말 7]

 

① $ - \sqrt {3} \leq a \leq \sqrt {3} $

② $ - \sqrt {3} <a< \sqrt {3} $

③ $ -2 \sqrt {2} \leq a \leq 2 \sqrt {2} $

④ $ -2<a<2 $

⑤ $ - \sqrt {2} <a< \sqrt {2} $

 

 

27. 좌표평면 위에서 반지름의 길이가 $ 1 $인 원 $ \mathrm C $가 곡선 $ y=\ln x $와 $ y $축에 동시에 접할 때 원 $ \mathrm C $와 곡선 $ y=\ln x $의 접점을 $ \mathrm P $라 한다. 점 $ \mathrm P $의 $ x $좌표를 $ a $라 할 때, $ a ^ {3} -2a ^ {2} +2a $의 값을 구하여라.[5점]

[2015 과고3 1학기 기말 8]

 

 

28. 원점을 중심으로 하는 반지름 $ 1 $인 원 $ x ^ {2} +y ^ {2} =1 $ 위의 세 점 $ \mathrm P ( 1,~0) $, $ \mathrm Q ( \cos \theta ,~\sin \theta ) $, $ \mathrm R ( \cos \theta ,~-\sin \theta ) $ $ \left ( 0< \theta < \frac {\pi } {2} \right ) $있다. 이 세점에서 접선을 그어 생기는 도형은 이등변삼각형이다. 이 세 점 $ \mathrm {P,~Q,~R} $을 지나는 외접원의 반지름을 $ r=r ( \theta ) $라 할 때, $ \lim\limits _ {r \rightarrow 0} {r ( \theta )} $의 값을 구하여라.[5점]

[2015 과고3 1학기 기말 10]

 

 

29. 반지름의 길이가 $ 1 $인 원 $ O $ 위에 한 점 $ \mathrm A $가 있다. 점 $ \mathrm A $를 중심으로 하고 반지름의 길이가 $ r $인 원이 원 $ O $와 만나는 점을 각각 $ \mathrm {P,~Q} $라 하고 원 $ O $의 지름 $ \mathrm {AB} $과 만나는 점을 $ \mathrm R $라 하자. $ \mathrm {\triangle APR} $의 넓이를 $ S ( r) $라고 할 때, $$ \lim\limits _ {r \rightarrow 0} { \frac {S ( r)} {r ^ {2} } } $$의 값을 구하여라.(단, $ 0<r<2 $) [5.3점]

[2015 과고3 1학기 기말 11]

 

 

 

30. $ 0 \leq x<2 \pi $의 구간에서 두 곡선 $ y=a-\cos 2x $와 $ y=2\sin x $가 서로 접할 때, 상수 $ a $의 값들의 곱을 구하여라.[5.0점]

[2015 과고3 1학기 기말 12]

 

 

31. $ a $는 $ 1 $이 아닌 양의 상수이고, $ x _ {0} =1 $, $ n=1,~2,~3,~ \cdots $에 대하여 $ x $축 위의 점 $ ( x _ {n-1} ,~0) $에서 곡선 $ y=a ^ {x} $에 근은 접선의 접점을 $ ( x _ {n} ,~y _ {n} ) $이라고 한다. 무한급수 $ \sum\limits _ {n=1} ^ {\infty } \frac {1} {y _ {n} } $의 값을 구하여라. [5.0점]

[2015 과고3 1학기 기말 13]

 

 

 

32. $ p,~q $는 $ p+q=1 $ ($ 0 \leq p \leq 1 $)을 만족하는 임의의 실수라 할 때, 함수 $ g ( x)= \sqrt {x} $에서 $$ g ( px+qy) \geq p \cdot g ( x)+q \cdot g ( y) $$이 성립함을 증명하시오.(단, $ x \geq 0,~y \geq 0 $) [8점]

[2015 과고3 1학기 기말 서술1]

 

 

 

33. 다음 삼각함수의 극한 $$ \lim\limits _ {x \rightarrow 0} { \frac {1-\cos x} {\sin ^ {2} x} } $$을 구하여라.[4.7점]

[2015 과고3 2학기 중간 2]

 

 

34. $ \frac {1-\tan ^ {2} \frac {x} {2} } {1+\tan ^ {2} \frac {x} {2} } = \frac {1} {2} $일 때, $ \sin \frac {x} {2} $의 값을 구하여라. (단, $ 0 \leq x<2 \pi $)(4.7점)

[2015 과고3 2학기 중간 3]

 

 

35. 함수 $ f ( x)=xe ^ {-x} $에 대하여 $ f ( x) $의 $ n $계 도함수 $ f ^ { ( n)} ( x) $의 극값을 $ a _ {n} $이라고 할 때, 무한급수 $ \sum\limits _ {n=1} ^ {\infty } a _ {n} $의 값을 구하여라.(단, $ e $는 자연로그의 밑)［5.3점]

[2015 과고3 2학기 중간 10]

 

 

36. $ \alpha \neq k \pi $ ($ k $는 정수)일 때, $$ \lim\limits _ {n \rightarrow \infty } {\left ( \cos \frac {\alpha } {2} \cos \frac {\alpha } {2 ^ {2} } \cos \frac {\alpha } {2 ^ {3} } \cdots \cos \frac {\alpha } {2 ^ {n} } \right )} $$의 값을 구하여라.[5점]

[2015 과고3 2학기 중간 4]

 

 

37. $ x $에 관한 이차방정식 $ 9x ^ {2} -15x+8=0 $의 두 근이 $ \sin 2 \theta ,~\cos 2 \theta $이다. 이차방정식을 만족하는 $ \theta $에 대하여 $ \tan \theta $의 모든 값을 합하여라. [2.8점]

[2016 과고1 2학기 중간 미적분2 16]

 

 

38. 모든 실수 $ x,~y $에 대하여 $ 2x ^ {2} +3y ^ {2} =4 $가 성립할 때, $ x ^ {2} +y ^ {2} +xy $의 최댓값을 구하여라. [3.0점]

[2016 과고1 2학기 중간 미적분2 18]

 

 

39. $$ \cos x+\cos 3x+\cos 5x+ \cdots +\cos ( 2n-1)x $$를 간단히 하시오.

[2016 과고1 2학기 중간 미적분2 서술형 6]

https://youtu.be/r1yDpbXkhI0

 

 

40. 곡선 $ y=ax ^ {2} $이 곡선 $ y=\ln x $에 접하도록 상수 $ a $의 값을 구하여라. [2.7점]

[2016 과고2 심화수학II 1학기 기말 1]

 

 

41. $$ \lim\limits _ {x \rightarrow \frac {\pi } {2} } { \frac {a ( 2x- \pi )\cos x+b} {\sin x-1} } $$을 만족하는 상수 $ a,~b $에 대하여 $ a+b $의 값을 구하여라.[2.7점]

[2016 과고2 심화수학II 1학기 기말 2]

 

 

42. $ x>-1 $에서 정의된 함수 $ f ( x)= \root {3} \of { ( x+1) ( x ^ {2} +1)} $의 역함수 $ g ( x) $에 대하여 $$ \lim\limits _ {n \rightarrow \infty } {2n \left\{ g \left ( 1+ \frac {1} {n} \right ) -g \left ( 1- \frac {1} {n} \right ) \right\} } $$의 값을 구하여라.[3점]

[2016 과고2 심화수학II 1학기 기말 4]

 

 

43. 포물선 $ y= \frac {1} {4} x ^ {2} $ 위의 두 점 $ \mathrm P \left ( \sqrt {2} ,~ \frac {1} {2} \right ) $, $ \mathrm Q \left ( a,~ \frac {a ^ {2} } {4} \right ) $에서의 두 접선과 $ x $축으로 둘러싸인 삼각형이 이등변삼각형일 때, 상수 $ a ^ {2} $의 값을 구하여라.(단, $ a> \sqrt {2} $)[2.9점]

[2016 과고2 심화수학II 1학기 기말 6]

 

 

44. 원점에서 곡선 $$ y= ( x-a)e ^ {-x} $$ (단, $ a \neq 0 $)에 오직 하나의 접선을 그을 수 있을 때, $ a ^ {2} $의 값을 구하여라. [2.9점]

[2016 과고2 심화수학II 1학기 기말 7]

 

 

45. 함수 $ f ( x)=2\sin x+\cos x $와 구간 $ ( - \infty ,~ \infty ) $에서 미분가능한 두 함수 $ g ( x),~h ( x) $에 대하여 $ p ( x)= ( h \circ g \circ f) ( x) $라고 하자. $ p ' ( 0)=6 $일 때, $$ h ' ( g ( 1))g ' ( 1) $$의 값을 구하여라.[2.9점]

[2016 과고2 심화수학II 1학기 기말 8]

 

 

46. 곡선 $ y= \frac {x ^ {2} +ax+b} {x ^ {2} -1} $이 변곡점이 $ ( 2,~5) $일 때, 상수 $ a,~b $에 대하여 $ a+b $의 값을 구하여라.[3점]

[2016 과고2 심화수학II 1학기 기말 9]

 

 

 

47. 곡선 $ y=\ln x $ 위의 점 $ ( t,~\ln t) $에서의 접선과 $ x $축, $ y $축으로 둘러싸인 삼각형의 넓이의 최댓값을 구하여라. (단, $ 0<t<e $)[3점]

[2016 과고2 심화수학II 1학기 기말 10]

 

 

 

 

49. $ \mathrm {\triangle ABC} $에서 $ \mathrm {\overline {AB}} =1 $이고 $ \angle A= \theta ,~ \angle B=2 \theta $이다. $ \mathrm {\angle ACD=2 \angle BCD }$가 되도록 변 $ \mathrm {AB} $ 위의 점 $ \mathrm D $를 잡을 때, $$ \lim\limits _ {\theta \rightarrow 0+} { \frac {\mathrm {\overline {CD}} } {\theta } = \frac {b} {a} \sqrt {3} } $$이다. $ a ^ {2} +b ^ {2} $의 값을 구하여라. (단, $ 0< \theta <\frac {\pi } {4} $이고, $ a,~b $는 서로소인 자연수이다.)[3.1점]

[2016 과고2 심화수학II 1학기 기말 11]

 

 

50. $ k>0 $일 때, 함수 $ f ( x)=kx ^ {2} e ^ {-x} $에 대하여 곡선 $ y=f ( x) $ 위의 점 $ ( t,~f ( t)) $에서 $ x $축까지의 거리와 $ y $축까지의 거리 중 크지 않은 값을 $ g ( t) $라고 하자. 함수 $ g ( t) $가 한 점에서만 미분가능하지 않도록 하는 $ k $의 최댓값을 구하여라. [3.1점]

[2016 과고2 심화수학II 1학기 기말 12]

https://youtu.be/58SpYFEe09c

 

 

51. $ x>0 $일 때, 다음 부등식을 증명하여라.[5점]

$$ \frac {1} {x+1} <\ln ( x+1)-\ln x< \frac {1} {x} $$

[2016 과고2 심화수학II 1학기 기말 서술1]

 

 

 

52. $ n $을 양의 정수라고 할 때, 함수 $$ f _ {n} ( x)=n\ln x+ \frac {n+1} {x} -n\cos \frac {1} {n} $$에 대하여 $ 0<x< \infty $에 있어서 $ f _ {n} ( x) $의 증감을 조사하고 최솟값을 $ a _ {n} $이라고 할 때, $$ \lim\limits _ {n \rightarrow \infty } {a _ {n} } $$을 구하여라.[5점]

[2016 과고2 고급수학II 2학기 기말 서술8]

 

 

 

 

53. $$ \lim\limits _ {x \rightarrow \pi } {} \frac {\sqrt {a+\cos x} -b} { ( x- \pi ) ^ {2} } = \frac {1} {4} $$가 되도록 상수 $ a,~b $를 정할 때, $ a ^ {2} +b ^ {2} $의 값을 구하여라.[2.7점]

[2016 과고2 고급수학II 2학기 중간1]

 

 

54. 원점을 중심으로 하는 반지름 $ 1 $인 원 $ x ^ {2} +y ^ {2} =1 $ 위에 점 $ \mathrm {P ( 1,~0),~Q ( \cos \theta ,~\sin \theta ),~R ( \cos \theta ,~-\sin \theta )} $ ($ 0< \theta <\frac {\pi } {2} $)를  잡는다. $ \mathrm {P,~Q,~R} $을 접점으로 하는 세 개의 원의 접선에 의하여 생기는 이등변삼각형을 그려 그 외접원의 반지름을 $ r=r ( \theta ) $라고 하자. $$ \lim\limits _ {\theta \rightarrow 0} {r ( \theta )} = \frac {b} {a} $$라고 할 때, $ a ^ {2} +b ^ {2} $의 값을 구하여라. (단, $ a,~b $는 서로소인 자연수)[3점]

[2016 과고2 고급수학II 2학기 중간9]

 

 

55. 자연수 $ m,~n $에 대하여 함수 $ f ( x) $가 다음과 같이 실수 전체에서 정의되어 있을 때, 다음 물음에 답하시오.

$$ f ( x)= { \begin {cases} x ^ {m} \sin \frac {1} {x ^ {n} } &( x \neq 0)\\0 &( x=0)\end {cases} } $$

[2017 과고1 미적분II 2학기 중간 8]

1) $ f ( x) $가 $ x=0 $에서 연속이기 위한 자연수 $ m,~n $의 조건을 구하시오.[1점]

2) $ m=n=1 $일 때, 함수 $ f ( x) $가 $ x=0 $에서 미분가능 여부를 밝히시오.[1점]

3) $ f ( x) $가 $ x=0 $에서 미분가능이기 위한 자연수 $ m,~n $의 조건을 구하시오.[2점]

4) $ f ( x) $의 도함수가 $ x=0 $에서 연속이기 위한 자연수 $ m,~n $의 조건을 구하시오.[2점]

 

https://youtu.be/UIrAVpUhl-M

 

 

56. 다음 삼각방정식의 해를 구하시오. 단, $ 0 \leq x \leq 2 \pi $이다.(답만 맞으면 정답인정함) [4점]

[2017 과고1 미적분II 2학기 중간 11]

1) $ \sin ( \pi \cos x)=0 $ [2점]

2) $ \cos x-\sin x=\cos 2x $ [2점]

 

 

 

57. 다음 함수의 그래프를 그리고, 최댓값, 최솟값과 주기를 구하시오. 단, 정의역은 $ \left\{ x|- \pi \leq x \leq 3 \pi \right\} $이다. 답만 맞으면 정답 인정함) [5점]

[2017 과고1 미적분II 2학기 중간 12]

$$ y=\sin x- \left | \cos x \right | $$

 

 

 

58. $ x>1 $에서 증가하고 미분가능한 함수 $ f ( x) $가 있다. $ f ( 3)=1,~f ' ( 3)=2 $이고 $ f ( x ^ {2} +1) $ (단, $ x>0 $)의 역함수를 $ g ( x) $라고 할 때, $ g ' ( 1) $의 값을 구하시오.(답만 맞으면 정답 인정함)[3점]

[2017 과고1 미적분II 2학기 중간 13]

https://youtu.be/pzjHYh5gWeY

 

 

59. 다음 그림에서 $ \mathrm {\overline {AB}} =3 $, $ \mathrm {\overline {BC}} =5 $, $ \mathrm {\overline {AD}} =8 $, $ \mathrm {\angle CAB}= \theta $라 하자. 점 $ \mathrm C $가 $ \mathrm {\overline {AD} }$위를 움직일 때, $$ \lim\limits _ {\theta \rightarrow 0+} { \frac {\mathrm {\overline {CD}} } {\theta ^ {2} } } $$의 값을 구하시오.[4점]

[2017 과고1 미적분II 2학기 중간 14]

 

 

60. 좌표평면 위에 두 점 $ \mathrm {A ( 2,~5),~B ( 4,~3)} $가 있다. 점 $ \mathrm P ( \cos \theta ,~\sin \theta ) $에 대하여 $ \mathrm {\overline {PA} ^ {2} + \overline {PB} ^ {2}} $의 최댓값과 최솟값의 차를 구하시오. [4점]

[2017 과고1 미적분II 2학기 중간 15]

https://youtu.be/vu8Vo7Owd6k

 

 

61. 두 실수 $ x,~y $에 대하여 다음 세 조건을 만족시킬 때, $ \tan ( x+y) $의 값을 구하시오.[4점]

[2017 과고1 미적분II 2학기 중간 16]

(가) $ 0<x< \frac {\pi } {2} ,~0<y< \frac {\pi } {2} $

(나) $ \sin x\sin y= \frac {\sqrt {2} } {4} $

(다) $ \cos ^ {2} x+\cos ^ {2} y= \frac {5} {4} $

 

 

 

62. 다음 물음에 답하시오.

[2017 과고2 고급수학II 2학기 중간 1]

(1) $ \lim\limits _ {x \rightarrow 0} { \frac {1-\cos x} {x ^ {2} } } $를 구하시오.[1점]

(2) 함수 $ f ( x) $는 $ x=1 $에서 미분가능하다고 한다. (1)의 결과를 사용하여 $$ \lim\limits _ {x \rightarrow 0} { \frac {f ( 2-\cos x)-f ( 1)} {x ^ {2} } } $$을 $ f ' ( 1) $을 써서 나타내어라.[2점]

 

 

63. 다음 그림을 보고 물음에 답하여라.(단, 사각형 $ \mathrm {ACDE} $, $ \mathrm {ABGF} $, $ \mathrm {BCIH} $는 각각 변 $ \mathrm {AC} $, $ \mathrm {AB} $, $ \mathrm {BC} $를 한 변으로 하는 정사각형이고, 점 $ \mathrm {P,~Q,~R} $은 각각 점 $ \mathrm {A,~B,~C} $에서 변 $ \mathrm {HL,~DE,~GF }$에 그은 수선의 발이며, 점 $ \mathrm {L,~M,~N} $은 각각 선분 $ \mathrm {BC} $와 $ \mathrm {AP} $, $ \mathrm {AC} $와 $ \mathrm {BQ} $, $ \mathrm {AB} $와 $ \mathrm {RC} $의 교점이다. $ \mathrm {\overline {BC}} = a $, $ \mathrm {\overline {AC}} = b $, $ \mathrm {\overline {AB} }= t c $, $ \mathrm {\angle BAC}= \theta $라 하고, $ \mathrm {\angle BAC} $는 예각이다.)

[2017 과고1 미적분II 2학기 중간 19]

1) 사각형 $ \mathrm {LCIP} $의 넓이와 사각형 $ \mathrm {MCDQ} $의 넓이가 같음을 증명하시오.[3점]

2) (1)의 성질을 이용하여 $ a ^ {2} =b ^ {2} +c ^ {2} -2bc\cos \theta $를 증명하시오.[2점]

3) $ \mathrm {\angle BCA} $가 둔각일 때 위와 같은 그림을 그리고, $ a ^ {2} =b ^ {2} +c ^ {2} -2bc\cos \theta $를 증명하시오.[4점]

https://youtu.be/wZJbyDhyg-U

 

 

64. $ \mathrm {A+B+C}= \pi $일 때 다음 등식이 성립함을 증명하시오.[6점]

$$\begin{align} & \sin ^ {3} \mathrm A+\sin ^ {3} \mathrm B+\sin ^ {3} \mathrm C \\&=3\cos \left ( \frac {\mathrm A } {2} \right ) \cos \left ( \frac {\mathrm B } {2} \right ) \cos \left ( \frac {\mathrm C } {2} \right ) -\cos \left ( \frac {\mathrm 3A } {2} \right ) \cos \left ( \frac {\mathrm 3B } {2} \right ) \cos \left ( \frac {\mathrm 3B } {2} \right ) \end{align} $$

(힌트: $ \sin 3 \theta =3\sin \theta -4\sin ^ {3} \theta $, $ \cos 3 \theta =4\cos ^ {3} \theta -3\cos \theta $)

[2017 과고1 미적분II 2학기 중간 20]

https://youtu.be/r6Y8pBO6Cxs

 

 

65. 함수 $ f ( x) $는 미분가능하고, 다음 조건을 (a), (b)를 만족할 때, 다음 물음에 답하시오.

[2017 과고2 고급수학II 2학기 중간 2]

(a) $ f ( x) \geq x+1 $

(b) 모든 실수 $ h $에 대하여 $ f ( x+h) \geq f ( x)f ( h) $

(1) $ f ( 0)=1 $임을 보여라.[2점]

(2) $ f ' ( 0)=1 $임을 보여라.[2점]

 

https://youtu.be/MuIqaO8DMyw

 

66. 다음 물음에 답하시오.

[2017 과고2 고급수학II 2학기 중간 3]

(1) 다음 부등식이 성립함을 증명하시오.[3점]

$$ \frac {1} {x} <\ln \frac {x} {x-1} <\frac {1} {x-1} $$

(단, $ x>1 $)

(2) 임의의 양의 정수 $ m $에 대하여 $$ \sum\limits _ {k=n} ^ {mn} \frac {1} {k} $$을 구하여라.[2점]

(3) 위의 결과를 이용하여 $$ \lim\limits _ {n \rightarrow \infty } {\sum\limits _ {k=1} ^ {2n} ( -1) ^ {k-1} \frac {1} {k} =\ln 2} $$임을 증명하여라.[2점]