[수학의 기초] 기저와 기저변환 행렬

기저와 기저변환행렬이란?

선형대수학 또는 고등학교 과정의 기하와 벡터 단원에서 기저(basis)란 용어가 등장한다.
중$\cdot$고등과정에서 좌표를 말할 때, 그 속에서는 기저라는 내용이 암묵적으로 들어가 있다. 예를 들어 $\mathrm P(2,~3)$이란 좌표를 말할 때는 다음과정이 진행된다.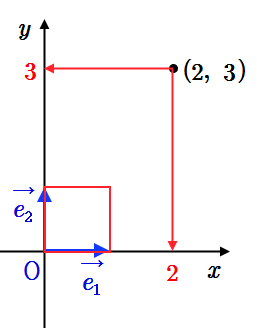

먼저 원점(Origin)을 먼저 생각하고 원점을 지나는 서로 수직인 두 개의 축을 생각했을 때, 흔히 우리는 $x$축, $y$축을 말한다. $\mathrm P$의 좌표가 $(2,~3)$이란 말은 점 $\mathrm P$에서 $x$축에 내린 수선의 발의 눈금을 읽으면 $2$이고 $y$축에 내린 수선의 발의 눈금이 $3$이란 말이다. 이 눈금을 순서로 읽어서 $(2,~3)$으로 적는다. 여기서 순서로 쌍을 괄로로 묶는다는 말이 순서쌍(ordered pair)이란 말이다. 무엇을 먼저 읽느냐의 순서가 정해졌다는 말이다.
여기서 말한 눈금 $2,~3$을 읽기 위해서는 먼저 읽는 단위를 먼저 결정해야 한다. 이 단위를 결정하는 것이 기저-basis라는 말이다. 위의 그림에서 좌표평면에서 원점 $\mathrm O$에서 $(1,~0)$으로 가는 벡터를 $\overrightarrow {e_1}$, $(0,~1)$로 가는 벡터를 $\overrightarrow {e_1} $를 기저(basis)라고 정하고 이것을 기준으로 해서 좌표 $(2,~3)$을 $\overrightarrow{p}=2\overrightarrow{e_1}+ 3 \overrightarrow{e_2}$로 표시한다. 
크기가 $1$이고 $x$축, $y$축의 양의 방향으로 향하는 벡터 $\overrightarrow {e_1} $, $\overrightarrow {e_2} $를 basis로 하면 우리가 알고 있는 좌표가 벡터와 일대일 대응된다. 이 때의 두 벡터를 표준기저(Standard basis vector)라고 한다.
물론 기저를 $\overrightarrow {e_1} $, $\overrightarrow {e_2} $로 잡을 필요는 없다. 좌표평면에서는 평행하지 않고 $\overrightarrow 0$가 아닌 두 벡터를 잡아도 기저가 된다. 왜 기저가 되는지 또 기저가 무엇이고 차원이 무엇인지는 다음 기회에 설명하겠다.

만약 위의 벡터를 표현할 때, 기저를 $\overrightarrow {a}=(1,~0)$과 $\overrightarrow b =(1,~3)$으로 잡으면 $\overrightarrow{p}=2\overrightarrow{e_1}+ 3 \overrightarrow{e_2}$는 $1\overrightarrow{a}+1  \overrightarrow{b}$로 된다. 이 때의 $(1,~1)$은 기저를 $\overrightarrow {a}=(1,~0)$와 $\overrightarrow b =(1,~2)$에 대한 상대적 좌표이다. 즉
$$\overrightarrow{p}=2\overrightarrow{e_1}+ 3 \overrightarrow{e_2}= 1\overrightarrow{a}+ 1 \overrightarrow{b}$$
기저에 따른 좌표표현 방법에 대해 알아보자.
$2$차의 유클리드 벡터공간-보통 우리가 사용하는 좌표평면-에서 표준기저 집합을 $S=\left\{ \overrightarrow{e_1}= \left[ \matrix{1\\0}\right],~\overrightarrow{e_2}=\left[\matrix{0\\1} \right] \right\}$이라 했을 때,
$$\overrightarrow{p}=2\overrightarrow{e_1}+3\overrightarrow{e_2}= 2 \left[\matrix{1\\0}\right]+3 \left[\matrix{0\\1}\right]$$
로 나타낼 때,
$$ \left[\overrightarrow{p}\right]_S=\left[\matrix{2\\3}\right]$$
마찬가지로 기저 집합을 $B=\left\{ \overrightarrow a=\left[ \matrix{1\\0}\right],~\overrightarrow b=\left[\matrix{1\\3} \right] \right\}$이라 했을 때,
$$\overrightarrow{p}=1\overrightarrow{a}+1\overrightarrow{b}= 1 \left[\matrix{1\\0}\right]+1 \left[\matrix{1\\3}\right]$$
로 나타낼 때,
$$ \left[\overrightarrow{p}\right]_B=\left[\matrix{1\\1}\right]$$
 
동일한 벡터 $\overrightarrow {p}$가 기저가 다름에 따라 좌표가 달라진다. 즉 $(2,~3)$에서 $(1,~1)$로!!
 
기저변환행렬에 대해 알아보자.  처음 이 용어를 접했을 때, 기저를 바꾸는 행렬이 무엇인지 애매했다. $\mathbb{R^2}$에서 생각하자. 기저변환행렬이란 기저를 $\overrightarrow{a},~\overrightarrow{b}$로 했을 때 임의의 벡터 $\overrightarrow {p}$의 상대적 좌표 $(x,~y)$를 $\overrightarrow{a'},~\overrightarrow{b'}$로 했을 때의 상대적 좌표 $(x',~y')$로 바꾸는 행렬을 의미한다. 즉
$$  \overrightarrow{p}=x \overrightarrow a +y \overrightarrow{b} =x' \overrightarrow {c}+y' \overrightarrow {d}  $$
처음의 기저 $\overrightarrow a ,~\overrightarrow b$가 나중의 기저 $\overrightarrow {a'} ,~\overrightarrow {b'}$로 각각
$$ \begin{align} \overrightarrow{a}=p \overrightarrow {a'} +r \overrightarrow{b'} \\ \overrightarrow {b} =q \overrightarrow {a'}+s \overrightarrow {b'} \end{align} $$
로 표현되었을 때, 기저변환행렬은
$$\left[ \matrix{p&q\\r&s} \right]$$
 
예를 들어 위의 경우를 생각하면 표준기저에서의 좌표를 $(x,~y)$라 하고 기저집합 $B=\left\{ \overrightarrow a=\left[ \matrix{1\\0}\right],~\overrightarrow b=\left[\matrix{1\\3} \right] \right\}$에서의 좌표를 $(x',~y')$이라 하면 동일한 벡터가 기저에 따라 다르게 표현되므로
$$x \left[\matrix{1\\0}\right]+ y \left[\matrix{0\\1}\right]=x' \left[\matrix{1\\0}\right]+ y' \left[\matrix{1\\3}\right] $$
이것을 연립방정식의 형태로 쓰면
$$\begin{align} x&=x'+y'\\y&=3y'\end{align}$$
$$\left[ \matrix{1&0\\0&1} \right] \left[ \matrix{x\\y } \right]  = \left[\matrix{1&1\\0&3} \right] \left[ \matrix{x'\\y'} \right]$$
따라서
$$ \begin{align} \left[ \matrix{x'\\y' } \right]  &= \left[\matrix{1&1\\0&3} \right]^{-1} \left[ \matrix{x\\y} \right] \\ &=\frac{1}{3}  \left[\matrix{3&-1\\0&1} \right]  \left[ \matrix{x\\y} \right] \end{align} $$
이다. 이 때, 행렬 $\frac{1}{3}  \left[\matrix{3&-1\\0&1} \right]$을 기저변환행렬이라 하고 $ \left[ P \right]_{E}^{B}$로 나타낸다. 즉 기저집합 $E$에서의 좌표를 기저 $B$에서의 좌표로 바꾸는 행렬을 의미한다.
위에서 본 표준기저 $E$에서의 $\overrightarrow p$의 좌표 $(2,~3)$을 기저집합 $B=\left\{ \overrightarrow a=\left[ \matrix{1\\0}\right],~\overrightarrow b=\left[\matrix{1\\3} \right] \right\}$에서의 좌표로 표현하려면 기저변환행렬 $ \left[ P \right]_{E}^{B}$에 좌표 $(2,~3)$을 곱하면 기저 $B$에서의 좌표로 표현된다. 즉
$$ \begin{align} \left[ P \right]_{E}^{B} \left[\matrix{2\\3}\right] &= \frac{1}{3}  \left[\matrix{3&-1\\0&1} \right]\left[\matrix{2\\3}\right] \\&= \left[\matrix{1\\1}\right] \end{align}$$
 
기저를 바꾼다는 말은 축을 바꾼다는 말과 같다. 비슷한 예로 고등학교 과정에서 "좌표축을 옮기는 과정은, 축을 놓아두고 좌표를 거꾸러 옮기는 과정과 같다." 는 것을 들어 본적이 있을 것이다. 이 말이 위의 기저변환행렬을 구하는 과정에서 왜 역행렬을 구하는 것이 표준기저에서 기저 B로 옮길 때 일어나는 지 설명해보자. 예를 들어
기저 벡터 $\overrightarrow a =(2,~3),~\overrightarrow b =(1,~2)$를 표준기저 $\overrightarrow e_1 =(1,0),~\overrightarrow e_2 =(0,~1)$로 바꾼다는 말의 의미는
$\overrightarrow a =(2,~3)$의 좌표가 $(1,~0)$에서 $(2,~3)$으로 옮겨졌다는 것이다.
이것의 이해가 핵심이다. 기저변환 역시 일차변환의 한 종류이고 일차변환에서는 $(1,~0)$과 $(0,~1)$이 옮겨진 좌표를 알면 곧바로 행렬을 구할 수 있다. 여기서 $\overrightarrow a =(2,~3)$가 기저를 $\overrightarrow a =(2,~3),~\overrightarrow b =(1,~2)$로 했을 때의 $(1,~0)$이기 때문이다. 정말 햇갈린다.

기저를 벡터 $\overrightarrow a =(2,~3),~\overrightarrow b =(1,~2)$로 했을 때, 좌표 $(1,~0),~(0,~1)$이 표준기저 $\overrightarrow{e_1},~\overrightarrow{e_2}$로 했을 때의 각각의 좌표는 다음과 같이 바뀐다. 즉
$$\begin{align} (1,~0) ~\Rightarrow~ (2,~3)\\(0,~1)~\Rightarrow ~(1,~2) \end{align}$$
따라서
$$\begin{align} \left[ \matrix{2\\3}\right]= Q \left[ \matrix{1\\0} \right] \\ \left[ \matrix{1\\2}\right]= Q \left[ \matrix{0\\1} \right]  \end{align}$$
$$\therefore ~Q= \left[ \matrix{2&1\\3&2} \right] $$
즉 행렬 $Q$는 기저를 벡터 $\overrightarrow a =(2,~3),~\overrightarrow b =(1,~2)$로 했을 때의 좌표 표현을 좌표 $(1,~0),~(0,~1)$이 표준기저 $\overrightarrow{e_1},~\overrightarrow{e_2}$로 했을 때의 좌표표현으로 바꾸는 행렬이다.
보통 일차변환에서 $(1,~0)$이 $(a,~c)$로, $(0,~1)$이 $(b,~d)$로 옮겨진다면 일차변환의 행렬표현은 $$ \left[ \matrix{a&b\\c&d} \right] $$이지만 기저 벡터 $ (a,~c),~ (d,~d)$를 표준기저 $(1,0),~(0,~1)$로 바꿀 때의 행렬표현은 $$ \left[ \matrix{a&b\\c&d} \right] $$이다. 그 반대이다. 이해가 되었기를 바란다.
기저를 구성하는 벡터내부의 좌표에 신경쓰지 말고 기저의 표현에 신경쓰면 된다. ㅠㅠ
$$\textcolor{red}{p}  (\textcolor{blue}{1,~3})+\textcolor{red}{q} (\textcolor{blue}{4,~2})$$
파란색으로 표시된 좌표는 신경쓰지 말고  빨간색으로 표시된 좌표 $\textcolor{red}{(p,~q)}$가 어떻게 바뀌는지 신경쓰자.
 
 
[수학의 기초] 기저변환행렬 (2) [더플러스수학]
 
이해가 안되는 부분이 있거나 잘못 표현된 부분이 있으면 댓글로 남겨주세요. 추가 설명하거나 오류는 수정하겠습니다.
과학고 내신대비와 대학입시를 위해서는 다음의 글을 참조하세요. 다양한 글이 있습니다.

과고1학년, 2학년 대신대비를 위해 더플러스수학학원의 구술시스템에서 실제로 하고 있는 문제를 보시려거나 과학고 3학년 AP미적분학을 준비하고자 하거나 대학교1학년 미적분학에 대해 공부하려고 하면 더플러스수학 프리미엄콘텐츠 를 이용해 보세요.

https://naver.me/FsR64KUy

과학고전문더플러스수학 : 네이버 프리미엄콘텐츠

더플러스수학 https://www.youtube.com/@THEPLUSMATH/channels
더플러스수학 블로그 https://plusthemath.tistory.com/
더플러스수학 네이버블로그 https://m.blog.naver.com/plusthemath