[더플러스수학] 카탈란 수 - 일반항(2)

2021.08.02 - [수학과 공부이야기] - [더플러스수학] 카탈란 수 (1)

[더플러스수학] 카탈란 수 (1)

앞 편의 글에서 카탈란 수 \(\displaystyle C_n \)가 무엇인지 또, 실생활에서는 어떻게 활용되는지에 대해 알아 보았다.
이 편에서는 카탈란 수 \(\displaystyle C_n \)의 일반항이 어떤 과정을 거쳐서

\(\displaystyle C_n = \frac{1}{n+1} {}_{2n} \mathrm{C}_{n}= {}_{2n}\mathrm{C}_{n}-{}_{2n}\mathrm{C}_{n-1}\)

이 되는지 알아보자.
앞 편의 글 에서의 예인 \(\displaystyle 5,000\)원을 가진 사람을 \(\displaystyle A \), \(\displaystyle 10,000\)원을 가진 사람을 \(\displaystyle B \)라 하자. 입장을 할 수 있는 경우는 어떤 \(\displaystyle A \)에 대해서도 이 \(\displaystyle A \) 앞에서는 \(\displaystyle A \)의 개수보다 \(\displaystyle B \)의 개수가 더 많아서는 안된다.
여기서 우리는 여사건을 이용하여 계산하자. \(\displaystyle A \) \(\displaystyle 3 \)개, \(\displaystyle B \) \(\displaystyle 3 \)개를 나열하는 총 경우의 수

\(\displaystyle \frac{6!}{3!3!} ={}_6 \mathrm{C}_3 \)

에서 입장하지 못하는 경우의 수를 빼서 계산하겠다. 이 경우를 분류해보자.
먼저 제일 앞에 \(\displaystyle B \)가 오면 입장할 수 없다. 즉

\(\displaystyle \textcolor {red}{B} \times \times \times \times \times \)

이 때, \(\displaystyle \times \times \times \times \times \)에는 \(\displaystyle A \)가 \(\displaystyle 3 \)개, \(\displaystyle B \)가 \(\displaystyle 2 \)개 있으므로 나열하면

\(\displaystyle \frac{5!}{3! \times 2!}={}_5 \mathrm{C}_3 =10\)

하나의 예로 \(\displaystyle \textcolor {red}{B} \textcolor {blue}{AAABB} \)이 있다.
또, \(\displaystyle AB \textcolor {red}{B}  \times \times \times \)일 때도 입장할 수 없다. 이 경우에 \(\displaystyle \times \times \times \times \)에는 \(\displaystyle A \)가 \(\displaystyle 2 \)개, \(\displaystyle B \)가 \(\displaystyle 1 \)개 있으므로 나열하면

\(\displaystyle \frac{3!}{2! \times 1!}={}_3 \mathrm{C}_2 =3 \)

하나의 예로 \(\displaystyle AB\textcolor {red}{B} \textcolor {blue}{AAB} \)이 있다.
또, \(\displaystyle ABAB \textcolor {red}{B}  \times \)일 때도 입장할 수 없다. 이 경우에 \(\displaystyle \times  \)에는 \(\displaystyle A \)가 \(\displaystyle 1 \)개, \(\displaystyle B \)가 \(\displaystyle 0 \)개 있으므로 나열하면

\(\displaystyle \frac{1!}{1! \times 0!}={}_1 \mathrm{C}_1 =1\)

하나의 예로 \(\displaystyle ABAB\textcolor {red}{B} \textcolor {blue}{A} \)이 있다.
또, \(\displaystyle AABB \textcolor {red}{B}  \times \)일 때도 입장할 수 없다. 이 경우에 \(\displaystyle  \times \)에는 \(\displaystyle A \)가 \(\displaystyle 1 \)개, \(\displaystyle B \)가 \(\displaystyle 0 \)개 있으므로 나열하면

\(\displaystyle \frac{1!}{1! \times 0!}={}_1 \mathrm{C}_1 =1 \)

하나의 예로 \(\displaystyle AABB\textcolor {red}{B} \textcolor {blue}{A} \)이 있다.
따라서 구하는 경우의 수는

\(\displaystyle \frac{6!}{3!3!} ={}_6 \mathrm{C}_3 -15 =5\)개

이다.
여기서 입장할 수 없는 경우를 다시 관찰해보자. 위에서 구체적인 예로 든 경우에서 맨앞의 문자에서 빨간색 \(\displaystyle \textcolor {red}{B} \)까지의 문자를 \(\displaystyle A \)를 \(\displaystyle B \), \(\displaystyle B \) \(\displaystyle A \)로 바꿔서 아래처럼 정리해보자.

\(\displaystyle \textcolor {red}{B} \textcolor {blue}{AAABB} ~~\Longleftrightarrow ~~\textcolor {red}{A} \textcolor {blue}{AAABB} \)
\(\displaystyle AB\textcolor {red}{B} \textcolor {blue}{AAB} ~~\Longleftrightarrow ~~\textcolor {red}{BAA} \textcolor {blue}{AAB} \)
\(\displaystyle ABAB\textcolor {red}{B} \textcolor {blue}{A} ~~\Longleftrightarrow ~~\textcolor {red}{BABAA} \textcolor {blue}{A} \)
\(\displaystyle AABB\textcolor {red}{B} \textcolor {blue}{A} ~~\Longleftrightarrow ~~\textcolor {red}{BBAAA} \textcolor {blue}{A} \)

위의 오른쪽의 배열에서 빨간색은 고정되어 있고, 푸른색은 배열할 수 있으므로 이 총 경우의 수는 \(\displaystyle AAAABB\)를 배열한 경우의 수인 \(\displaystyle {}_6 \mathrm {C}_2 \) 또는 \(\displaystyle {}_6 \mathrm {C}_4 \)개다.
따라서 \(\displaystyle C_4={}_6 \mathrm {C}_3 - {}_6 \mathrm {C}_2 =5\)개다.
위의 과정에서 붉은 색 \(\displaystyle \textcolor {red}{B}\) 앞의 \(\displaystyle A\)와 \(\displaystyle B\)를 바꾼다는 것은 아래의 과정에서는 직선 \(\displaystyle {y=x+1}\)에 대칭이동한다는 것임을 염두에 두자.
 
위의 과정을 좀 더 다르게 접근하자.
\(\displaystyle A\)를 '\(\displaystyle \rightarrow \)'로, 즉 '오른쪽으로 한 칸' 옮기는 행위로, \(\displaystyle B\)를 '\(\displaystyle \uparrow \)'로, 즉 '위쪽으로 한 칸' 옮기는 행위로 바꾸면 \(\displaystyle A\)의 개수가 \(\displaystyle B\)개수보다 많야야 한다는 것은 직선 \(\displaystyle y=x\)의 위쪽으로 갈 수 없다는 것을 의미한다.
따라서 \(\displaystyle C_3 \)는 원점 \(\displaystyle \mathrm{O}(0,0)\)에서 직선 \(\displaystyle y=x\)의 위쪽으로 가지 않으면서 점 \(\displaystyle \mathrm{A}(3,3)\)으로 가는 최단 경로의 수를 의미한다.
그림으로 나타내면 아래와 같다.

또, 위에서 본

\(\displaystyle \textcolor {red}{B} \textcolor {blue}{AAABB} ~~\Longleftrightarrow ~~\textcolor {red}{A} \textcolor {blue}{AAABB} \)
\(\displaystyle AB\textcolor {red}{B} \textcolor {blue}{AAB} ~~\Longleftrightarrow ~~\textcolor {red}{BAA} \textcolor {blue}{AAB} \)
\(\displaystyle ABAB\textcolor {red}{B} \textcolor {blue}{A} ~~\Longleftrightarrow ~~\textcolor {red}{BABAA} \textcolor {blue}{A} \)
\(\displaystyle AABB\textcolor {red}{B} \textcolor {blue}{A} ~~\Longleftrightarrow ~~\textcolor {red}{BBAAA} \textcolor {blue}{A} \)

을 그림으로 차래대로 그리면 아래와 같다.

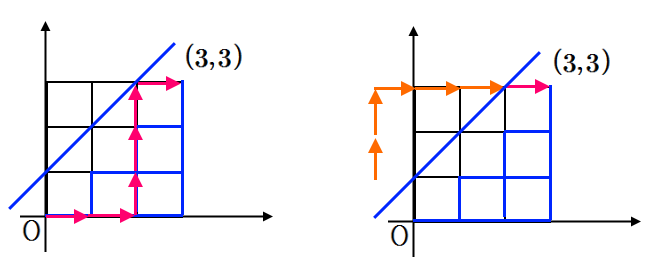
위의 그림에서 보듯이 원점 \(\displaystyle \mathrm {O}(0,0)\)에서 \(\displaystyle (3,3) \)까지로 가는 경로 중 카탈란 수 \(\displaystyle C_3 \)를 만족하지 않는 경로는 반드시 직선 \(\displaystyle y=x+1\)와 최초로 만나는 점 \(\displaystyle \mathrm {P}\)이 반드시 존재한다.  그리고 원점 \(\displaystyle \mathrm {O}(0,0)\)에서 점 \(\displaystyle \mathrm {P}\)까지 가는 경로를 직선 \(\displaystyle y=x+1\)에 대하여 대칭이동하면 점 \(\displaystyle \mathrm {O}'(-1, 1)\)에서 점 \(\displaystyle \mathrm {P}\)까지 가는 경로가 되고 또, 점 \(\displaystyle \mathrm {P}\)에서 \(\displaystyle (3,3)\)까지 가는 경로를 연결하면 결국 \(\displaystyle \mathrm {O}'(-1, 1)\)에서 \(\displaystyle (3,3)\)까지 가는 경로가  \(\displaystyle \mathrm O (0,0)\)에서  \(\displaystyle (3,3)\)까지의 경로 중 카탈란 수를 만족하는 않는 경로를 나타낸다. 위의 그림에서는 오른쪽 그림이다.
위의 과정을 일반화하여 카탈란 수의 일반항을 구해보자.
카탈란 수  \(\displaystyle C_n\)은 원점 \(\displaystyle \mathrm O (0,~0)\)에서 \(\displaystyle (n,~n)\)까지 직선 \(\displaystyle y =x\)를 넘지 않으면서 가는 최단 경로의 수이다.

따라서 직선 \(\displaystyle y =x\)를 넘으면서 \(\displaystyle (n,~n)\)까지 가는 경로의 수는 원점을 직선 \(\displaystyle y=x+1\)에 대하여 대칭이동한 점인 \(\displaystyle (-1,~1)\)에서 \(\displaystyle (n,~n)\)까지 가는 경로의 수이다. 즉

\(\displaystyle {}_{2n} \mathrm {C} _{n-1}= \frac{2n!}{(n-1)! \times (n+1)!}\)

이다. 

따라서 카탈란 수 \(\displaystyle C_n \)은

\(\displaystyle \begin{align} C_n &= {}_{2n} \mathrm{C}_n -{}_{2n} \mathrm{C}_{n-1} \\& =\frac{1}{n+1} {}_{2n} \mathrm{C}_n \end{align}\)

2021.08.03 - [수학과 공부이야기] - [더플러스수학] 카탈란 수 - 점화식(3)

[더플러스수학] 카탈란 수 - 점화식(3)

2021.08.06 - [수학과 공부이야기] - [더플러스수학] 카탈란 수 - 생성함수(4)

[더플러스수학] 카탈란 수 - 생성함수(4)

 
과고1학년, 2학년 대신대비를 위해 더플러스수학학원의 구술시스템에서 실제로 하고 있는 문제를 보시려거나 과학고 3학년 AP미적분학을 준비하고자 하거나 대학교1학년 미적분학에 대해 공부하려고 하면 더플러스수학 프리미엄콘텐츠 를 이용해 보세요.

https://naver.me/FsR64KUy

과학고전문더플러스수학 : 네이버 프리미엄콘텐츠