[더플러스수학학원] 직선이 평면을 분할하는 개수, 평면이 공간을 분할하는 개수, 원이 평면을, 구가 공간을 분할하는 개수에 대하여 [울산과고기출]

울산옥동에 있는 울산과고 전문 더플러스수학학원입니다. 이번에는 수열에 관한 울산과학고 기출문제에 대해 알아보려고 합니다. 직선이 평면을 최대 몇개로 분할하는지? 평면이 공간을 최대 몇개로 분할하는지에 대해 원리를 알아보고, 이것의 응용으로 원이 평면을 분할하는 개수, 차원을 높여 구가 공간을 몇개로 분할하는지에 대해 알아보고자 합니다.

먼저 울산과학고에서 2024년 1학년 2학기 중간고사에 다음과 같은 문제가 나왔습니다.

6. 다음을 보고 물음에 답하시오 [총 5점]

(가) 평면 위의 하나의 원은 평면을 두 개로 분할한다.

(나) 공간에서 하나의 구는 공간을 두 개로 분할한다.

(1) $\displaystyle n$ 개의 원이 한 평면을 최대로 분할하는 개수를 $\displaystyle a_n$ 이라고 하자. $\displaystyle a_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [2점]

(2) $\displaystyle n$ 개의 구가 한 공간을 최대로 분할하는 개수를 $\displaystyle b_n$ 이라고 하자. $\displaystyle b_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [3점]

 

이 문제를 풀기 위해 문제를 먼저

원을 직선으로! 구를 평면으로!

바꿔서 문제를 해결해 보자. 즉, 문제를

다음을 보고 물음에 답하시오 [총 5점]

---

(가) 평면 위의 하나의 직선은 평면을 두 개로 분할한다.

(나) 공간에서 하나의 평면는 공간을 두 개로 분할한다.

---

(1) $\displaystyle n$ 개의 원이 한 평면을 최대로 분할하는 개수를 $\displaystyle a_n$ 이라고 하자. $\displaystyle a_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [2점]

(2) $\displaystyle n$ 개의 구가 한 공간을 최대로 분할하는 개수를 $\displaystyle b_n$ 이라고 하자. $\displaystyle b_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [3점]

 

평면을 직선으로! 직선을 점으로!

 

먼저 위의 문제를 한 차원 낮추어 "평면"을 "직선"으로 "직선"을 "점"으로 바꿔 다음과 같이 바꾸자.

직선 위의 하나의 점은 직선을 두 개로 분할한다.

---

$\displaystyle n$ 개의 점이 한 직선을 최대로 분할하는 개수를 $\displaystyle a_n$ 이라고 하자. $\displaystyle a_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오.

---

먼저 직선 위에 $n $ 개의 점이 추가되면 $n +1$개의 선분으로 직선을 분할한다. 즉, $n$개의 점으로 직선을 $n+1$의 선분으로 분할한다. $n$개의 점으로 직선을 분할하는 선분의 개수를 $a_n$이라 하면 점화식으로 쓰면 

$$a_0=1,~a_{n+1}= a_n + 1$$

이를 풀면 (조합으로 표현한 이유는 나중에 최종 결론은 아름답게 내기 위한 것임)

$$a_n= a_0+\sum_{k=0}^{n-1} 1= 1+n = {}_n \mathrm C_0 +{}_n \mathrm C_1$$

* Note : 조합으로 쓰기 위해 점화식을 $a_0 =1,~a_{n+1}=a_n +1$로 하였다. 이하 모두 동일하다. 고등학교 방식으로 다시 적으면

$a_1=2,~a_{n+1}= a_n + 1$, $\displaystyle a_n= a_1+\sum_{k=1}^{n-1} 1= 2+(n-1)=1+n$

** 여기서 "점"이 "직선"을 분할한다. 즉, 점이 하나 추가되면 직선을 하나 더 분할한다. 예를 들어 보면

일차원인 직선에서 점을 하나 추가하면 직선이 하나더 분할되듯이 이것을 이차원으로 확장하면 "선분"이 하나 추가되면 "평면"이 하나더 분할된다. 다음의 그림을 참조하자.

점에 의해 직선이 하나 더 분할 되듯이 선분이 하나 더 추가됨에 따라 위의 그림에서 보듯이 영역이 1개였던 부분이 영역이 추가되어 2개가 되었다. 여기서 주의해야 하는 것은 직선이 아니라 선분이 하나 추가됨에 따라 영역이 1개 더 추가된다는 것이다.

직선이 1개 추가되면 선분이 몇개 더 추가되는지 보면 추가된 선분의 개수만큼 영역이 추가된다. 이해가 잘 될지? 즉, 위의 그림을 직선이 추가되는 것으로 그림을 그리면 다음과 같다.

물론 위에서 영역이 무한하므로 파란색으로 칠해진 선분은 선분이 아니라 반직선을 의미하지만 그냥 선분으로 말한다.

이제 1차원에서 한 것을 2차원으로 확장해 보자. 

새로운 직선 $l_3$이 추가됨에 따라 추가된 선분의 개수는 $3$개이다. 그 이유는 기존의 $2$개의 직선과 직선 $l_3$가 만나는 점의 개수는 ${}_2 \mathrm C _1 =2$개 이므로 이 $2$개의 점에 의해 위의 1차원에서 했듯이 $l_3$를 $3={}_2 \mathrm C_0 +{}_2 \mathrm C_1 $개의 선분으로 분할한다. 따라서 이 선분 $3$개는 영역을 $3$개 더 추가한다. 즉, 일차원에서 점이 추가됨에 따라 선분이 몇개로 분할되는지가 2차원에서 영역이 몇개 더 추가되는지가 결정된다. ㅠㅠ

이제 이를 일반화하면 직선 $l$개에 의해 평면이 분할되는 영역의 최대의 개수를 $b_n$이라 하면 $b_0=1$, 즉 직선이 하나도 없으면 평면은 $1$개의 영역으로 분할된다.

직선 $n+1$개의 직선으로 평면이 분할된 영역의 최대의 개수 $b_{n+1}$에 대해 점화식을 고찰해보자.

아래 그림에서 보듯이 먼저 직선 $n$개의 직선으로 평면이 최대한 분할되어 있다고 하자. 여기에 직선 $l_{n+1}$을 추가한다고 하자.

추가된 영역의 개수는 직선 $l_{n+1}$에 의해 추가된 선분의 개수만큼 더 생긴다. 그리고 추가된 선분의 개수는 직선 $l_{n+1}$이 추가됨에 따라 만들어진 점의 개수에 의해 결정된다. 즉 $a_n=n+1={}_n \mathrm C_0 + {}_{n} \mathrm C_1$이다.

따라서 점화식은

$$b_0=1,~b_{n+1}=b_n +a_n ,~ a_n = n+1 ={}_n \mathrm C_0 +{}_n \mathrm C_1 $$

이다.  일반항을 구하면

$$ \begin{aligned}b_n &= b_0+ \sum_{k=0}^{n-1} a_k = 1+ \sum_{k=0}^{n-1} {k+1}\\&= 1+ \frac{n(n-1)}{2} + n \\&= {}_n \mathrm C_0 +{}_n \mathrm C_1 + {}_n \mathrm C_2 \end{aligned}$$

이다.

이제 2차원에서 3차원으로 확장하자.

또 다시 반복하자.

일차원에서는 직선 위에 추가된 점의 개수가 직선을 추가적으로 분할하는 선분의 개수를 결정한다.

또, 이차원에서는 직선이 새롭게 추가됨에 따라 만들어진 선분의 개수가 추가된 영역의 개수를 결정한다.

이제 3차원에서는 새로이 추가된 평면에 의해 만들어진 평면 위에 나누어진 영역의 개수가 추가된 공간의 영역의 개수를 결정한다. 

예를 들어 아래와 같은 만약 세 평면으로 공간을 나눠져 있다고 가정하자. 삼각형 $\mathrm{PQR}$로 이루어진 평면 $\pi_1$, 삼각형 $\mathrm{PRS}$로 이루어진 평면 $\pi_2$, 삼각형 $\mathrm{PSQ}$로 이루어진 평면 $\pi_3$로 공간이 나눠져 있다고 하면,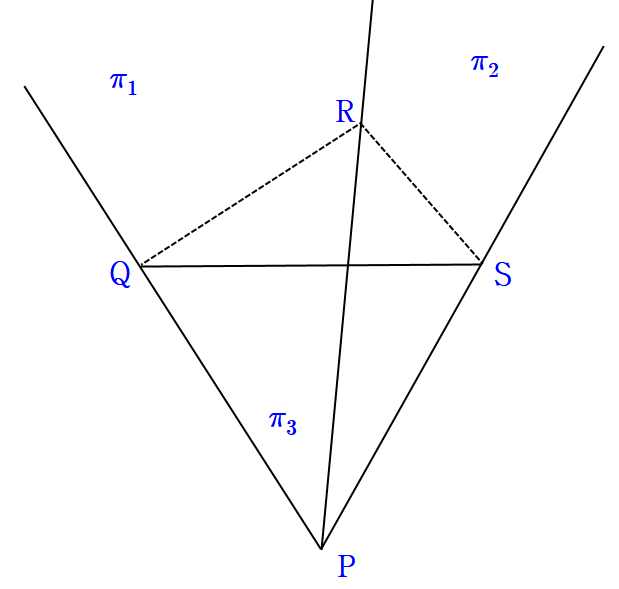

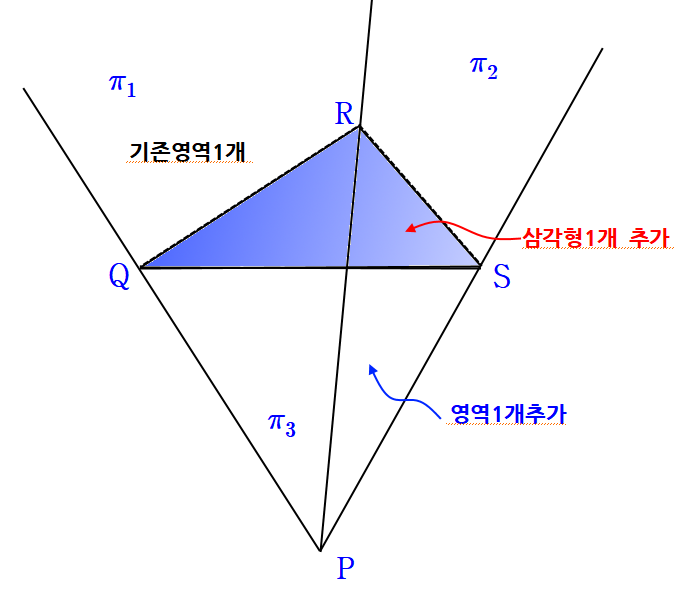
예를 들어 여기에서 세 점 $\mathrm{Q,~R,~S}$를 지나는 삼각형으로 공간을 분할한다면 위의 공간은 삼각뿔 $\mathrm {PQRS}$로 이루어진 영역과 그 밖의 무한한 영역으로 나누어 진다. 따라서 새로운 영역이 하나 추가된다.

이를 통해 새로운 평면 $\pi_4$가  기존의 평면 ($\pi_1 ,~\pi_2 ,~\pi_3$)과 만나서 생기는 영역의 개수만큼 공간을 나눈다. 왜냐하면 기존공간의 영역을 평면의 영역(위에서는 삼각형)으로 나눠 새롭게 하나 더 생기게 만든다. 공간적으로 생각해보세요.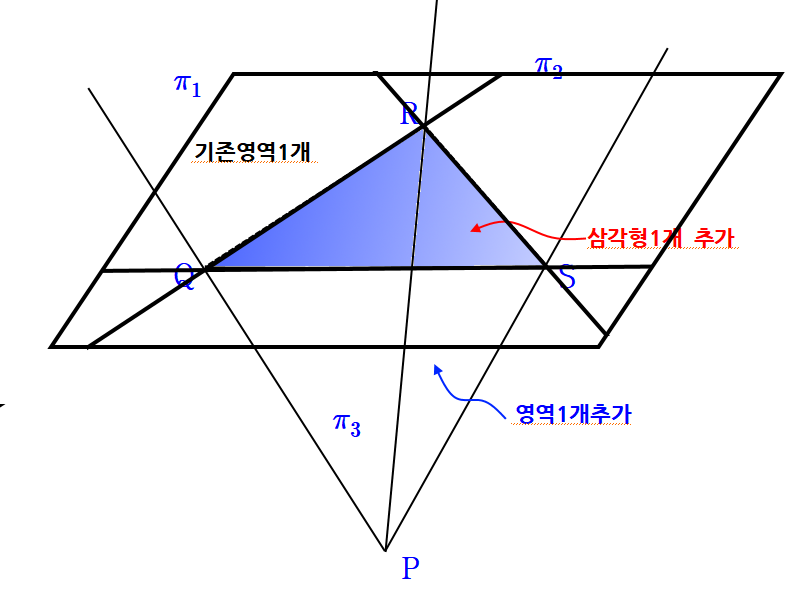 

교선 $\mathrm {QR,~RS,~SQ}$로 세 점 $\mathrm {QRS}$을 지나는 평면을 어떻게 나누는지를 그림으로 나누면 아래와 같다. 아래 그림에서 만들어진 영역의 개수가 새로 생기는 공간에서의 영역의 개수이다. 즉, $7$개 이다.

이 과정을 일반화하여 아래 그림에서 직선으로 보이는 $\pi_1 ,~\pi_2 ,~\pi_3 ,~\cdots p_{n-1},~\pi_n $는 모두 평면이고 파란색의 $\pi_{n+1}$은 새롭게 추가된 평면이라고 생각하자. 그러면 아래 그림에서 직선처럼 보이는 평면에 의해 새롭게 추가된 영역은 $b_{n}$이다. 그림을 유심히 잘 봅시다. 입체로 그리기에는 글쓴이가 능력이 없어. 죄송

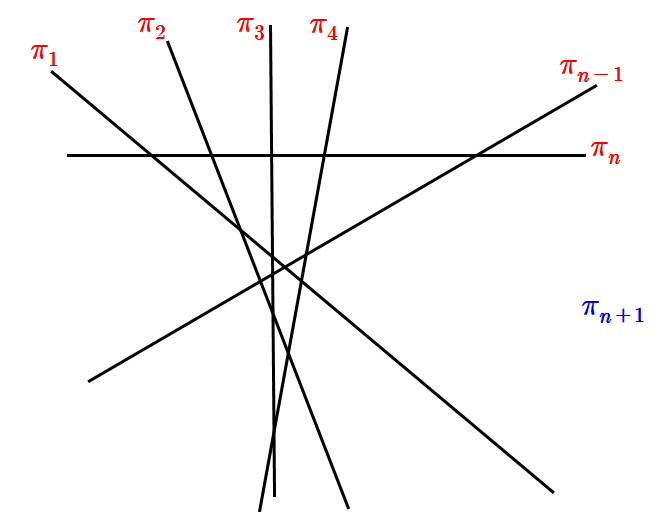
$n$개의 평면으로 공간이 최대한 나눠지는 영역의 개수를 $c_n$이라 하면 점화식은 다음과 같이 표현된다.

$$c_0=1,~c_{n+1} =c_n + b_n= c_n + {}_n \mathrm C_0 +{}_n \mathrm C_1 + {}_n \mathrm C_2 $$

이를 풀면

$$\begin{aligned} c_{n} &=c_0 +\sum_{k=0}^{n-1} b_k \\&= 1+ \sum_{k=0}^{n-1} \left\{{}_k \mathrm C_0 + {}_k \mathrm C_1 + {}_k \mathrm C_2 \right\} \\&= 1+{}_n \mathrm C_1 + {}_n \mathrm C_2 + {}_n \mathrm C_3\\&= {}_n \mathrm C_0+{}_n \mathrm C_1 + {}_n \mathrm C_2 + {}_n \mathrm C_3 \end{aligned}$$

즉, $c_{n}  = {}_n \mathrm C_0+{}_n \mathrm C_1 + {}_n \mathrm C_2 + {}_n \mathrm C_3 $

 

위의 과정을 정리해보면 일차원인 직선에서 점을 $n$개를 추가하면 직선이 분할되는 개수 $ a_{n} = {}_n \mathrm C_0+{}_n \mathrm C_1$이다. 왜 위와 같이 될까?  $   {}_n \mathrm C_0$은 $n$개의 점 중 $0$개를 선택하는 것은 그냥 직선 자체로  $1$개,  $   {}_n \mathrm C_1$은 $n$개의 점 중 $1$개를 선택한 개수만큼 선분이 만들어 진다.

또, 이차원인 평면에서 직선을 $n$개를 추가하면 평면이 분할되는 개수 $ b_{n} = {}_n \mathrm C_0+{}_n \mathrm C_1 +{}_n \mathrm C_2$이다.

$   {}_n \mathrm C_0$은 $n$개의 직선 중 $0$개를 선택하는 것은 그냥 평면 그 자체로  $1$개,  $   {}_n \mathrm C_1$은 $n$개의 직선 중 $1$개를 선택한 개수만큼 영역이 만들어 진다. 또, $   {}_n \mathrm C_2$은 $n$개의 직선 중 $2$개를 선택한 개수는 직선이 만나는 점의 개수만큼 영역이 생긴다. 즉 평면 하나, 직선의 개수만큼, 만나는 점의 개수만큼 평면이 분할 된다.

또, 삼차원인 평면에서 평면을 $n$개를 추가하면 공간이 분할되는 개수 $ c_{n} = {}_n \mathrm C_0+{}_n \mathrm C_1 +{}_n \mathrm C_2 +{}_n \mathrm C_3$이다.

$   {}_n \mathrm C_0$은 $n$개의 평면 중 $0$개를 선택하는 것은 그냥 공간 그 자체로  $1$개,  $   {}_n \mathrm C_1$은 $n$개의 평면 중 $1$개를 선택한 개수만큼 영역이 만들어 진다. 또, $   {}_n \mathrm C_2$은 $n$개의 평면 중 $2$개를 선택한 개수는 평면이 만나는 직선의 개수만큼 영역이 생긴다. 또, 세 평면이 만나서 생기는 점의 개수만큼 영역이 더 생긴다. 즉 공간, 평면의 개수, 직선의 개수만큼, 만나는 점의 개수만큼 공간이 분할 된다.

위의 내용을 기반으로 이제 울산과고문제를 풀어보자.

6. 다음을 보고 물음에 답하시오 [총 5점]

---

(가) 평면 위의 하나의 원은 평면을 두 개로 분할한다.

(나) 공간에서 하나의 구는 공간을 두 개로 분할한다.

---

(1) $\displaystyle n$ 개의 원이 한 평면을 최대로 분할하는 개수를 $\displaystyle a_n$ 이라고 하자. $\displaystyle a_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [2점]

(2) $\displaystyle n$ 개의 구가 한 공간을 최대로 분할하는 개수를 $\displaystyle b_n$ 이라고 하자. $\displaystyle b_n$ 을 $\displaystyle n$ 에 대한 식으로 나타내시오. [3점]

 

(풀이) (1) $n$개의 원이 평면을 나누는 개수  $\displaystyle a_n$ 이라 하자.

$a_1=2$

$n$개의 원이 있다고 할 때, $n+1$번째의 원을 그리면 기존의 $n$개의 원과 각각 $2$개씩 만나므로 총 $2n$개의 점으로 만나고 이 $2n$개의 점이 $n+1$번째의 원을 $2n$개의 호로 나누므로 추가적으로 더 나누어진 영역의 수는 $2n$개 이다. 따라서 점화식은

$\displaystyle a_{n+1} = a_n + 2n$

이를 풀면 

$$\begin{aligned} a_{n} &=a_1 +\sum_{k=1}^{n-1} 2k \\&= 2+ \sum_{k=0}^{n-1} 2k\\&= 1+2\times \frac{n(n-1)}{2}\\&= n^2 -n+2\end{aligned}$$

(2) $\displaystyle n$ 개의 구가 한 공간을 최대로 분할하는 개수를 $\displaystyle b_n$이라 하자.

$b_1 = 2$

$n$개의 구이 있다고 할 때, $n+1$번째의 구을 그리면 기존의 $n$개의 구와 만나는 영역의 개수는 (1)에서 구한 $a_n$과 같으므로 점화식은

$\displaystyle b_{n+1} = b_n + a_n = b_n + n^2 -n+2$

이를 풀면 

$$\begin{aligned} b_{n} &=b_1 +\sum_{k=1}^{n-1} (k^2 -k+2) \\&= 2+ \frac{n(n-1)(2n-1)}{6} -\frac{n(n-1)}{2} +2(n-1) \end{aligned}$$