[수학의 기초] 구점원, 오일러 직선, 세르보어 정리 — 자소서 탐구 주제(1)

울산과학고를 준비하는 중3이라면, 자기소개서에 단순한 성적 말고도 “내가 어떤 수학적 탐구를 했는가”를 보여주기 위해 자소서에 구점원, 오일러 직선, 세르보어 정리 등을 탐구주제로 선택합니다. 특히 울산 옥동에 있는 수학학원인 울산과고전문 더플러스수학학원에 자소서를 준비하는 학생들도 예외없이 이 주제를 선택했습니다.

이에 학생들이 스스로 문제들을 증명하여 소집면접 때 어떤 과정을 통해 이해했고, 거기서 무엇을 배웠는가에 대해 답변할 수 있게 최대한 자세히 증명과정을 서술하겠습니다. 한줄 한줄 잘 이해하기를 바랍니다. 이것은 외운다고 해결되지 않습니다.

먼저 구점원에 대해 알아보자.

(정의) 구점원(Nine-Point Circle, Euler Circle)
삼각형 $\displaystyle \mathrm{ABC}$에서 각 꼭짓점에서 대변에 내린 수선의 발을 각각 $\displaystyle \mathrm{D,~E,~F}$라 하고, 또, 세 변 $\displaystyle \mathrm{\overline{BC},~\overline{CA},~\overline{AB}}$의 중점을 각각 $\displaystyle \mathrm {P,~Q,~R}$이라 하자. 또, 수심 $\displaystyle \mathrm H$와 세 꼭짓점
$\displaystyle \mathrm{A,~B,~C}$의 중점을 각각 $\displaystyle \mathrm{L,~M,~N}$이라 하면 이 아홉개의 점
$\displaystyle \mathrm{D,~E,~F, ~P,~Q,~R,~L,~M,~N}$은 모두 하나의 원 위에 놓여있다.
이 원을 구점원(Nine-Point_Circle or Euler Circle)이라고 부른다.
또, 구점원의 중심은 삼각형의 외심 $\mathrm O$과 수심 $\mathrm H$의 중점에 위치한다. 구점원의 반지름은 외접원의 반지름의 $\displaystyle \frac 1 2$이다.

 

위의 그림에서 보듯이 삼각형 안에 특별한 9개의 점을 찍어보자.

1. 세 변의 한가운데 점(중점 $ 3 $ 개)
2. 세 꼭짓점에서 반대쪽 변으로 내린 수선이 만나는 점(발 $ 3 $ 개)
3. 꼭짓점과 삼각형 안의 수심을 연결했을 때, 그 중간에 있는 점(중점 $ 3 $ 개)

이렇게 총 $9 $ 개 점을 찍으면, 신기하게도 이 $ 9 $ 개 점이 하나의 원 위에 정확히 올라가게 됩니다. 이 원을 구점원이라고 부릅니다.

게다가 이 원의 중심은 “외심과 수심을 잇는 선분의 한가운데”에 있고, 반지름은 삼각형을 둘러싼 큰 원(외접원)의 반지름의 절반이다.

 

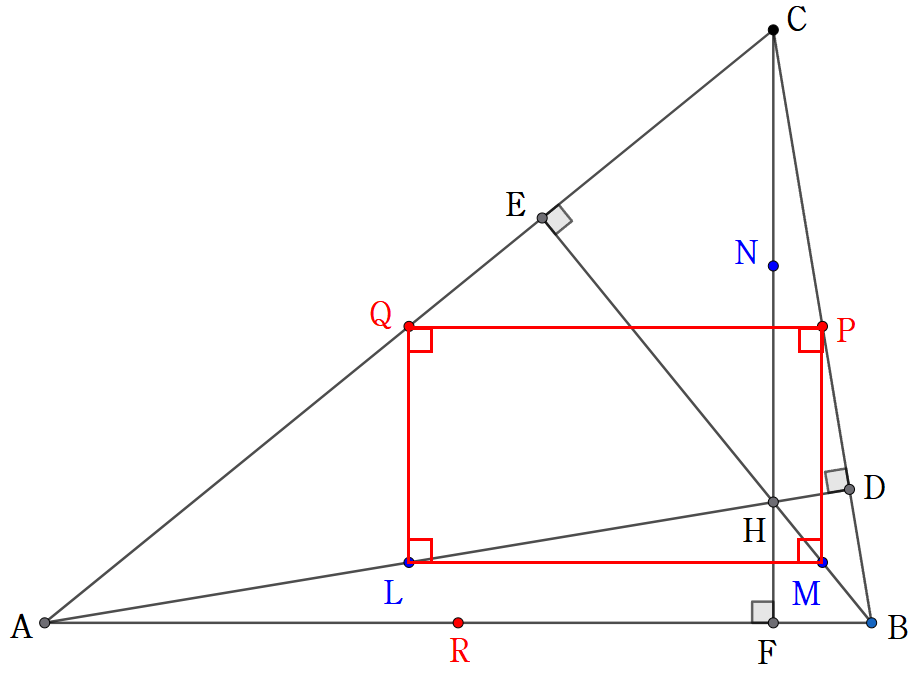
위의 그림에서 보듯이 먼저 사각형 $\displaystyle \mathrm{ LMPQ}$가 직사각형임을 보이자.

$\displaystyle \mathrm {AC}$의 중점 $\displaystyle \mathrm {Q}$, $\displaystyle \mathrm {AH}$의 중점 $\displaystyle \mathrm {L}$이므로 중점연결정리에 의해 $\displaystyle \mathrm {CF}$와 $\displaystyle \mathrm {QL}$은 평행하고

$\displaystyle \mathrm {\overline{QL}} = \frac{1}{2} \overline{\mathrm{CH}}$

또, $\displaystyle \mathrm {\triangle BHC}$에서 중점연결정리에 의해 $\displaystyle \mathrm {CH}$와 $\displaystyle \mathrm {PM}$은 평행하고

$\displaystyle \mathrm {\overline{PM}} = \frac{1}{2} \overline{\mathrm{CH}}$

또, $\displaystyle \mathrm {\triangle HAB}$와 $\displaystyle \mathrm {\triangle CAB}$ 에서 각각 중점연결정리에 의해 $\displaystyle \mathrm {AB}$와 $\displaystyle \mathrm {LM}$, $\displaystyle \mathrm { Q P}$ 은 평행하고 $\displaystyle \mathrm { CF}\bot \mathrm{AB}$이므로 사각형 $\displaystyle \mathrm{ LMPQ}$가 직사각형이다.

따라서 네 점  $\displaystyle \mathrm{ L,~M,~P,~Q}$은 대각선을 지름으로 하는 원 위에 존재한다. 

위의 그림에서 보듯이 $\displaystyle \mathrm {\angle QPM=\angle QEM=90^{\circ}}$, $\displaystyle \mathrm {\angle PML=\angle PQL=90^{\circ}}$이므로 이제 점 $\displaystyle \mathrm {D,~E}$도 동일한 원 위의 점이 된다.

한편 다음의 그림을 보자.

 

위의 그림에서 사각형 $\displaystyle \mathrm{ LMPQ}$가 직사각형임인 것과 동일한 이유로 사각형 $\displaystyle \mathrm{ LRPN}$도 직사각형이다. 따라서 아래 그림에서 보듯이 $\displaystyle \mathrm {\angle LRP=\angle LDP=90^{\circ}}$, $\displaystyle \mathrm {\angle NPR=\angle NFR=90^{\circ}}$이므로 이제 점 $\displaystyle \mathrm {D,~F}$도 동일한 원 위의 점이 된다.

이제 위의 원이 있는 두 그림을 동시에 아래와 같이 그려보자.

 

여기서 두 원의 지름이 공통으로 $\displaystyle \mathrm{\overline{LP}}$이므로 위의 두 원은 서로 같다. 즉, 9개의 점은 동일한 원 위에 존재한다. 즉 구점원이다. 그리고 선분 $\displaystyle \mathrm{\overline{LP}}$, $\displaystyle \mathrm{\overline{QM}}$, $\displaystyle \mathrm{\overline{NR}}$은 구점원의 지름이므로 각각의 선분의 중점이 구점원의 중심이 된다.

또, 구점원의 반지름의 길이는 삼각형 $\displaystyle \mathrm{ABC}$의 외접원의 반지름의 $\displaystyle \frac 1 2 $이다. 왜냐하면 아래 그림에서 보듯이 구점원은 삼각형 $\displaystyle \mathrm {PQR} $의 외접원이다. 그런데 삼각형 $\displaystyle \mathrm {ABC} $와 삼각형의 각변의 중점을 연결한 삼각형인  $\displaystyle \mathrm {PQR} $은 서로 닮았고 닮음비가 $2:1$이기 때문이다.

2025.09.01 - [수학과 공부이야기] - [수학의 기초] 구점원, 오일러 직선, 세르보어 정리 — 자소서 탐구 주제(2)