[더플러스수학] 2017년 가 교육청 7월 30번

상수항을 포함한 모든 항의 계수가 유리수인 이차함수 $ f ( x) $가 있다. 함수 $ g ( x) $가

$$ g ( x)= \left | f ' ( x) \right | e ^ {f ( x)} $$

일 때, 함수 $ g ( x) $는 다음 조건을 만족시킨다.

---

(가) 함수 $ g ( x) $는 $ x=2 $에서 극솟값을 갖는다.

(나) 함수 $ g ( x) $의 최댓값은 $ 4 \sqrt {e} $이다.

(다) 방정식 $ g ( x)=4 \sqrt {e} $의 근은 모두 유리수이다.

---

$ \left | f ( -1) \right | $의 값을 구하시오. [4점]

 

https://youtu.be/TlgOb62KUmM

 

 

 

 

정답 및 풀이를 보려면 아래를 클릭하세요.

 

정답 71

[출제의도] 미분을 활용하여 함수 추론하기

$ f ( x)=a ( x-m) ^ {2} +n $이라 하자.

$ f ' \left ( x \right ) =2a \left ( x-m \right ) $이고 $ f '' \left ( x \right ) =2a $이다.

두 곡선 $ y=f ( x) $와 $ y= \left | f ' ( x) \right | $는 각각 직선 $ x=m $에 대하여 대칭이므로

함수 $ g ( x)= \left | f ' \left ( x \right ) \right | e ^ {f ( x)} $의 그래프도 직선 $ x=m $에 대하여 대칭이다.

(ⅰ) $ x>m $인 경우$ a>0 $이면 함수 $ y=f ' \left ( x \right ) e ^ {f ( x)} $는 실수 전체에서 증가하므로 함수 $ g ( x) $의 최댓값이 존재하지 않는다.그러므로 조건 (나)에 의하여 $ a<0 $이다.

$ g ' \left ( x \right )  =- \left ( f ' \left ( x \right ) e ^ {f ( x)} \right ) ' $

$ g ' \left ( x \right ) =- \left [ f '' \left ( x \right ) + \left\{ f ' \left ( x \right ) \right\} ^ {2} \right ] e ^ {f ( x)} $$ g ' \left ( x \right )  = \left\{ -4a ^ {2} ( x-m) ^ {2} -2a \right\} e ^ {f ( x)} $

방정식 $ g ' \left ( x \right ) =0 $을 만족하는 $ x $는 한 개이고 그 값을 $ p $$ \left ( p>m \right ) $이라 하자. 함수 $ g \left ( x \right ) $는 $ x=p $에서 극댓값을 갖고, 그 값이 최댓값이다.

(ⅱ) $ x<m $인 경우함수 $ y=g ( x) $의 그래프는 직선 $ x=m $에 대하여 대칭이므로 함수 $ g \left ( x \right ) $는 $ x=2m-p $에서 극댓값을 갖고, 그 값이 최댓값이다.

(ⅰ), (ⅱ)에 의하여 함수 $ y=g ( x) $의 그래프의 개형은 다음과 같다.

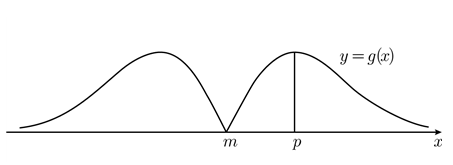
$ g ( m)=0 $이고, 함수 $ g ( x) $는 $ x=2 $에서 극솟값을 가지므로 $ m=2 $이다.

함수 $ g ( x) $는 $ x=p $에서 최댓값이 $ 4 \sqrt {e} $이므로

$ g ( p)= \left | f ' \left ( p \right ) \right | e ^ {f ( p)} =4 \sqrt {e} $

이다.

상수항을 포함한 모든 항의 계수가 유리수이므로

$ f ' \left ( p \right ) =2a ( p-2)=-4 $ …… ㉠

$ f ( p)=a \left ( p-2 \right ) ^ {2} +n= \frac {1} {2} $ …… ㉡

또한 함수 $ g ( x) $는 $ x=p $에서 극댓값을 가지므로 $ g ' \left ( p \right ) =0 $에서

$ 2a ( p-2) ^ {2} +1=0 $ …… ㉢

㉠, ㉡, ㉢에 의하여 $ n=1 $, $ p= \large \frac {9} {4} $이므로 $ a=-8 $

$ f ( x)=a ( x-m) ^ {2} +n=-8 ( x-2) ^ {2} +1 $

따라서 $ \left | f ( -1) \right | =71 $