[수학의 기초] 확률과 통계 경우의 수 구하는 특이한 방법들('menage problem'을 해결하기 위해)-1

 

 

1. $1$부터 $n$까지의 서로 다른 정수 중에서 이웃하지 않는 서로 다른 $k$를 뽑는 방법의 수는 $$\textcolor{red}{\displaystyle {}_{n-k+1} \mathrm{C}_{k}}$$

 

(증명) 서로 다른 $k$개의 수를 $x_1 ,~x_2 ,~\cdots,~x_k$라 두면 이 수들이 서로 이웃해서는 안되므로 $i=1,2,\cdots,{k-1}$인 $i$에 대하여 $x_i$ 와 $x_{i+1}$ 사이에는 적어도 $1$개의 숫자가 들어가야 한다. 그런데 $x_1$ 앞과 $x_k$ 뒤에는 $0$개 이상 들어 가도 된다.

$n$개 중 $k$개의 수가 아닌 것의 개수는 $n-k$개이다. 이 $n-k$개를 모두 같은 빈 $\boxed{~~}$ 로 표시하자.

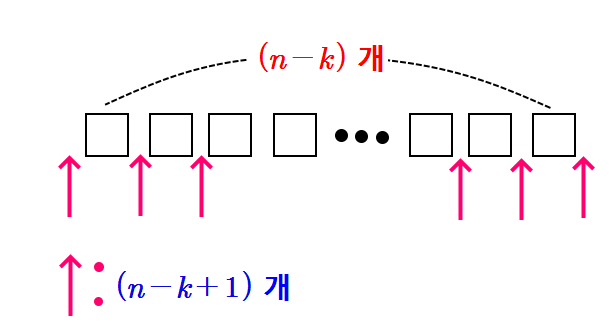
그러면 위의 그림에서 볼 수 있듯이 $\boxed{~~}$와 $\boxed{~~}$ 사이와 맨 앞과 맨 뒤 의 $n-k+1$개 중에 서로 다른 숫자가 들어갈 자리인 $k$개를 선택하면 된다. 즉 개수는

$$\displaystyle {}_{n-k+1} \mathrm{C}_{k}$$

 

다르게는 $x_1$앞에 들어갈 빈 $\boxed{~~}$의 개수를 $a_0$, $x_1$과 $x_2$사이에 들어갈 빈 $\boxed{~~}$의 개수를 $a_1$개, $\cdots$m  , $x_i$ 와 $x_{i+1}$ 사이에 들어갈 빈 $\boxed{~~}$의 개수를 $a_i$개라 하자. 또 $i$가 $i=1,2,\cdots,{k-1}$이므로 $x_k$ 뒤에 들어갈 빈 $\boxed{~~}$의 개수를 $a_{k}$개라 하자.

$$\displaystyle a_0 +a_1 + \cdots+a_k = n-k$$

여기서 $a_0 ,~a_k$는 $0$이상이고, $a_1 ,a_2 ,\cdots,a_{k-1} \ge1$이므로 $a_1 =a_1'+1$, $a_2 =a_2'+1$, $\cdots$, $a_{k-1} =a_{k-1}'+1$라 두면

$$\displaystyle a_0 +a_1' + \cdots+a_{k-1}'+a_k = n+1$$

이 방정식의 해의 개수는

$$\displaystyle {}_{k+1} \mathrm{H}_{n+1}={}_{n-k+1}\mathrm {C}_{n+1} ={}_{n-k+1}\mathrm{C}_{k}$$

이다.

 

2. $1$부터 $n$까지의 서로 다른 정수가 원탁 위에 있을 때, 이웃하지 않는 서로 다른 $k$를 뽑는 방법의 수는  $$\textcolor{red}{\displaystyle \frac{n}{n-k}{}_{n-k} \mathrm{C}_{k}}$$

 

(증명)