[삼사기출] 2017학년도 나형 14번-일대일대응

두 집합 $\displaystyle A= \left\{ 1,~2,~3,~4 \right\} $, $\displaystyle B= \left\{ 2,~3,~4,~5 \right\} $에 대하여 두 함수 $\displaystyle f~:~A \rightarrow B $, $\displaystyle g~:~B \rightarrow A $가 다음 조건을 만족시킨다.

(가) $\displaystyle f ( 3)=5 $, $\displaystyle g ( 2)=3 $ (나) 어떤 $\displaystyle x \in B $에 대하여 $\displaystyle g ( x)=x $이다. (다) 모든 $\displaystyle x \in A $에 대하여 $\displaystyle ( f \circ g \circ f) ( x)=x+1 $이다.

$\displaystyle f ( 1)+g ( 3) $의 값은? [4점] [2017년 사관학교 나형 14]

① $\displaystyle 5 $

② $\displaystyle 6 $

③ $\displaystyle 7 $

④ $\displaystyle 8 $

⑤ $\displaystyle 9 $

 

풀이) 아래 그림에서 보듯이 먼저 $g(4)=4$이어야 함을 보이기 위해 함수 $f,~g$가 일대일 대응임을 보이자.

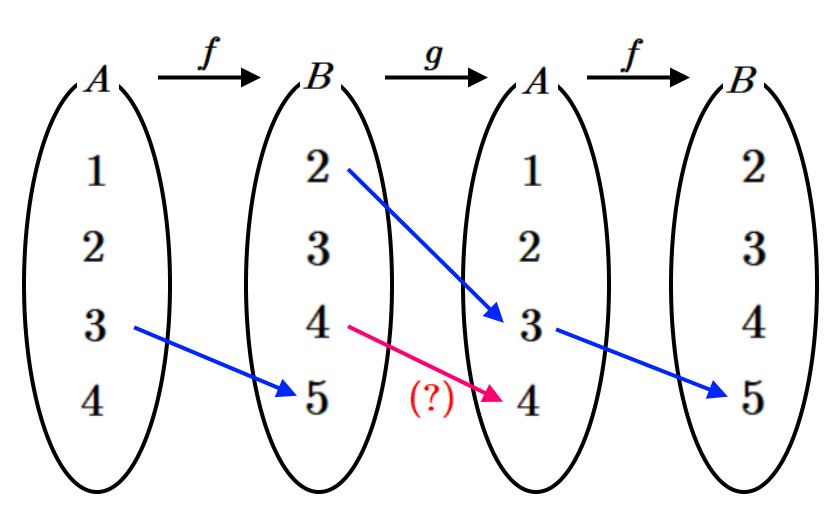
함수 $\displaystyle f~:~A \rightarrow B $, $\displaystyle g~:~B \rightarrow A $에 대해 조건 (다) "모든 $\displaystyle x \in A $에 대하여 $\displaystyle ( f \circ g \circ f) ( x)=x+1 $이다."를 만족한다는 사실에서 함수 $f$가 일대일 대응임을 먼저 보이자. (이전글 참조)

2020/03/27 - [수학과 공부이야기] - [수학의 기초] 함수에 대하여(1) - 함수의 정의와 합성

2020/03/29 - [수학과 공부이야기] - [수학의 기초] 함수에 대하여(2) - 함수의 종류

2020/03/29 - [수학과 공부이야기] - [수학의 기초] 함수에 대하여(3) - 일대일대응 역함수

1) 함수 $f$가 일대일함수이다.

(증명) 먼저 함수 $\displaystyle ( f \circ g \circ f) ( x)=x+1 $는 일대일함수이다. 즉 $y=x+1$은 일대일함수이다. (증명 생략)

여기서 함수 $f$가 일대일함수가 아니라고 가정하면 집합 $A$의 어떤 두 원소 $a,~b ~(a \neq b)$가 존재하여 $f(a)=f(b)$이다. 따라서 $$\displaystyle ( f \circ g) (f ( a))=(f \circ g )(f (b)) \Leftrightarrow ( f \circ g \circ f) ( a)= ( f \circ g \circ f) ( b) $$이다.

그런데 $\displaystyle ( f \circ g \circ f) ( a)=a+1 $, $\displaystyle ( f \circ g \circ f) ( b)=b+1 $이므로

$$b+1 =a+1 \Longleftrightarrow a=b$$

이것은 $a \neq b$에 모순이다.

2) 함수 $f$가 치역과 공역이 같은 함수이다.

(증명) 먼저 함수 $\displaystyle ( f \circ g \circ f) ( x)=x+1 $는 치역과 공역이 같은 함수이다. 즉 $y=x+1$은 치역과 공역이 같은 함수이다. (증명 생략)

여기서 함수 $f$가 치역과 공역이 같은 함수가 아니라고 가정하면 함수 $f$의 공역이 집합 $B$이므로

집합 $B$의 어떤 원소  $k$가 존재하여 $f$의 정의역의 임의의 원소 $x$에 대하여 $f(x) \neq k$ $~\cdots\cdots ~(\mathrm{i})$

즉 여기서 $k$는 함수 $f$에 대해 대응되지 않는 공역의 원소이다.

그런데 함수 $\displaystyle ( f \circ g \circ f) ( x)=x+1 $에 $x=k-1$을 대입하면

$$\displaystyle ( f \circ g \circ f) ( k-1)=(k-1)+1=k~\Longleftrightarrow ~f( (g \circ f)(k-1))=k $$

이다. 함수 $g \circ f$의 공역은 집합 $A$이므로 합성함수의 정의에 의해 $(g \circ f)(k-1) \in A$이다. 그런데 이것은 (i)과 모순이다. 

따라서 함수 $f$가 치역과 공역이 같은 함수이다.

 

또, 함수 $g$도 일대일 대응임을 보이자.

$h(x)=x+1$이라 하면 함수 $h ~:~A \rightarrow B$는 일대일 대응이다.  위에서 보였듯이 함수 $f$도 일대일대응이므로 역함수도 존재한다. 

$$\displaystyle \begin{align} ( f \circ g \circ f) ( x)=x+1 & \Longleftrightarrow ( f \circ g \circ f) ( x)=h \\&\Longleftrightarrow g= f ^{-1} \circ h \circ f^{-1} \end{align} $$

함수 $f,~h$가 일대일대응이므로 $f^{-1},~h$도 일대일대응이다. 따라서 함수 $g= f ^{-1} \circ h \circ f^{-1} $도 일대일대응이다. (증명은 이전글 참조)

2020/03/29 - [수학과 공부이야기] - [수학의 기초] 함수에 대하여(2) - 함수의 종류

 

함수 $g$가 일대일 대응이고 조건 (나)에서 $g(4)=4$이다.

가)에서 $\displaystyle f ( 3)=5, ~g ( 2)=3 $

다)에서

$\displaystyle x=4 $ 대입하면

$$\displaystyle \begin{align} ( f \circ g \circ f) ( 4)=5 ~&\Rightarrow ~ f ( (g \circ f)( 4))=5 \\& \Rightarrow (g \circ f ( 4))=3 \\ & \Rightarrow f ( 4)=2 \end{align}$$

$\displaystyle x=1 $ 대입하면

$$\displaystyle \begin{align} ( f \circ g \circ f) ( 1)=2 ~&\Rightarrow ~ f ( (g \circ f)( 1))=2 \\& \Rightarrow (g \circ f ( 1))=4 \\ & \Rightarrow f ( 1)=4 \end{align}$$

똑같은 방법으로

$\displaystyle x=3 $ 대입하면 $\displaystyle g ( 5)=1 $

$\displaystyle x=2 $ 대입하면 $\displaystyle f ( 2)=3,~g ( 3)=2 $

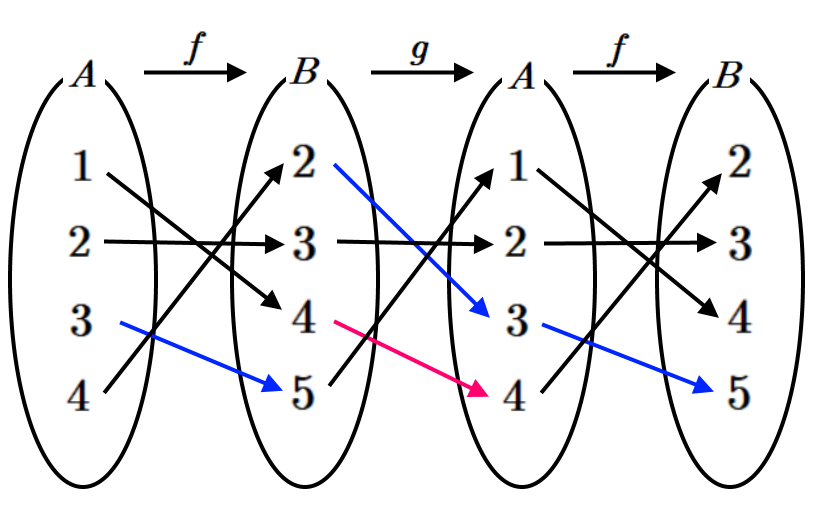
$\displaystyle \therefore f ( 1)+g ( 3)=4+2=6 $

따라서 이를 그림으로 나타내면 아래와 같다.