[더플러스수학] 카탈란 수 -활용(5)

 

이제 카탈란 수를 이용하여 경우의 수를 구하는 문제를 찾아보자.

문제1. 한국과 일본이 야구시합을 해서 한국이 $ 5 $대 $ 4 $로 이겼다. 한국이 일본에 리드를 당하지 않고서 즉, 이기거나 비길 수는 있어도 역적은 당하지 않은 채 시합에서 이길 경우의 수를 구하여라.

(풀이)

 

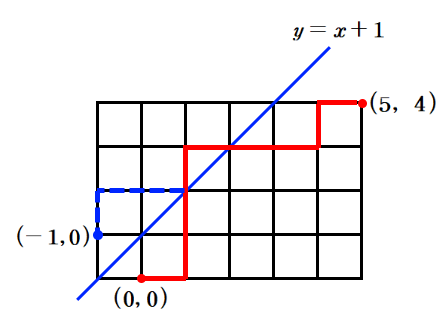
한국이 일본에 \(5\) 대 \(4\)로 이기는 총 경우의 수는 위의 그림에서 \((0,~0)\)에서 \((5,~4)\)에 도달하는 경우의 수

\(\displaystyle \frac{9!}{5! \times 4!}={}_9 \mathrm{C}_5 \)

이다. 이 경우의 수 중 역전을 허용하지 않으면서 \((5,~4)\)에 도달하려면 위의 경우에서 역전을 허용하면서 \( (5,~4)\)에 도달하는 경우의 수를 빼 주면 된다.

위의 그림에서 빨간 경로는 역전을 허용하면서 \((5,~4)\)에 도달하는 한 경로이다. 역전을 허용하는 경로는 항상 직선 \(y=x+1\) 과 최초로 만나는 경우가 있다. 직선 \(y=x+1\)와 최초로 만날 때까지의 경로를 직선 \(y=x+1\)에 대하여 대칭하면 결국 역전을 허용하여 \( (5,~4)\)에 도달하는 경로의 수는 점\( (-1,~1)\)에서 \( (5,~4)\)에 이르는 경로의 수와 같으므로 그 수는

\(\displaystyle \frac{9!}{6! \times 3!}={}_9 \mathrm{C}_6 \)

이다. 따라서 구하는 경우의 수는

\(\displaystyle \frac{9!}{5! \times 4!}- \frac{9!}{6! \times 3!}\)

이다.

 

 

문제2. 흰 바둑돌 $ 5 $개, 검은 바둑돌 $ 5 $개를 일렬로 나열할 때, 나열하는 순간 순간 마다 흰 바둑돌이 항상 검은 바둑돌보다 많거나 같은 것을 유지하면서 나열하는 방법의 수를 구하여라.

(풀이)

(풀이) 이 문제는 카탈란 수 \(C_5 \)와 같으므로

\(\displaystyle C_5 = \frac{1}{6} {}_{10} \mathrm {C}_5\)

이다.

 더플러스수학학원
울산 남구 대공원입구로21번길 45-1 2층
https://naver.me/xIhg4CMX

더플러스수학학원 : 네이버

 

더플러스수학학원 신정지점
울산 남구 문수로423번길 8 309호
https://naver.me/FTOL1Hgt

더플러스수학학원 신정지점 : 네이버