[더플러스수학] 3차함수의 접선의 갯수 [옥동수학학원]

3차함수의 접선이 개수

삼각함수 $\displaystyle f(x)=ax^3 +bx^2 +cx+d~( a > 0)$와 변곡점에서의 접선을 기준으로 평면 위의 점에서 삼차함수에 그을 수 있는 접선의 개수는 아래의 그림과 같다.
 

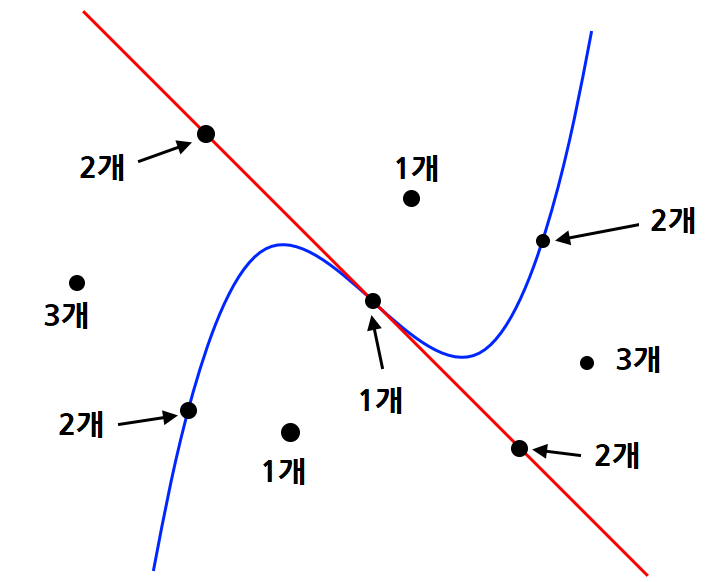
이것을 증명하기 위해 삼차함수의 변곡점을 $\displaystyle (\alpha,~\beta )$ 라 할 때,

$\displaystyle f''(x)=6a(x-\alpha)$

라 두면 적분을 통해

$\displaystyle f'(x)=3a(x-\alpha)^2 + b$
$\displaystyle f(x)=a(x-\alpha)^3 + b(x-\alpha)+ \beta$

로 표현할 수 있다. 여기서 $\displaystyle f(x)$를 $\displaystyle x$축으로 $\displaystyle -\alpha$, $\displaystyle y$축으로 $\displaystyle -\beta$만큼 평행이동한 함수를 $\displaystyle g(x)$라 하면 $\displaystyle g(x)$는

$\displaystyle g(x)=ax^3 +bx$

이다. $\displaystyle g(x)$의 변곡점의 좌표는 $\displaystyle (0,~0)$이고, 변곡점에서의 접선의 방정식 $\displaystyle l(x)$는 $\displaystyle l(x)=bx$이다.
이제 $\displaystyle (p,~q)$에서 곡선 $\displaystyle g(x)$에 그은 접점을 $\displaystyle (t,~g(t))$라 하면

$\displaystyle \frac{g(t)-q}{t-p}= g'(t)$
$\displaystyle g(t)-q= g'(t)(t-p)$
$\displaystyle g(t)- g'(t)(t-p)-q=0$

이다. 여기서 $\displaystyle (p,~q)$의 위치에 따라 위의 방정식의 근 $\displaystyle t$의 개수가 결정되는데 그 개수가 접선의 개수이다. 
$\displaystyle h(t)= g(t)- g'(t)(t-p)-q$라 두고 이 그래프의 개형을 그려보자.
먼저 미분하면 $\displaystyle h'(t)=g'(t)- g''(t)(t-p)-g'(t)=-g''(t)(t-p)=0$에서 

$\displaystyle g''(t)=0$ 또는 $\displaystyle  t=p$

$\displaystyle g(t)$의 변곡점의 좌표는 $\displaystyle (0,~0)$이므로 $\displaystyle h'(t)=0$의 근은

$\displaystyle t=0$ 또는 $\displaystyle t=p$

또, 여기서 $\displaystyle g(t)$의 최고차항의 계수 $\displaystyle a$는 양수이다.
첫째 $\displaystyle p>0$일 때, $\displaystyle y=h(t)$의 증감표를 그래프로 그리면 아래 그림과 같다.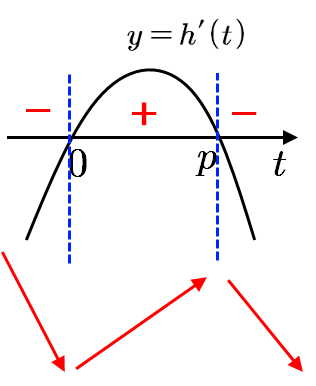 

변곡점 $\displaystyle (0, ~0)$에서의 접선이 방정식 $\displaystyle l(x)=g'(0)x$이다. 따라서 이 때 함숫값을 구하면

$\displaystyle \begin{align} h(0)&=g(0)-g'(0)((0-p)-q\\&=p g'(0)-q \\&=l(p)-q \end{align}$
$\displaystyle \begin{align} h(p)&=g(p)-g'(p)((p-p)-q\\&=g(p)-q \end{align}$

이다. 

 
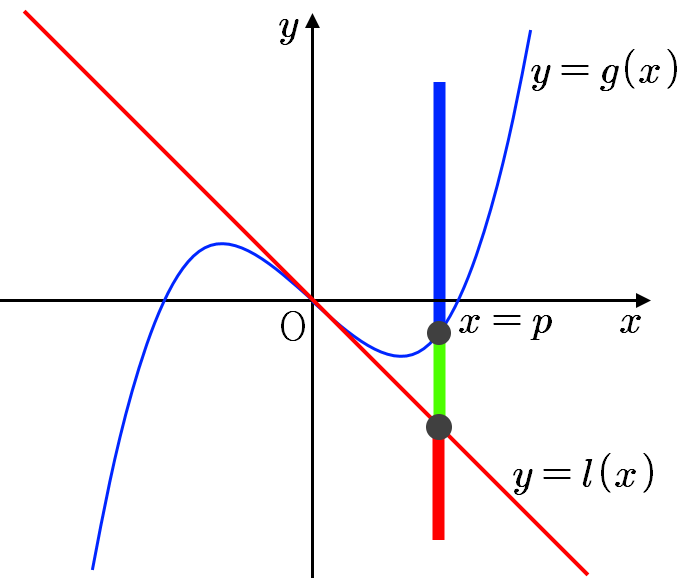
위의 그림에서 보듯이 점 $\displaystyle (p,~q)$가 파란색 범위에 있을 때, 즉 $\displaystyle q> g(p)$일 때
$\displaystyle q>l(p)$이므로 $\displaystyle  h(0) <0,~h(p)<0$이므로 $\displaystyle y=h(x)$의 극댓값과 극솟값이 모두 음이므로 $\displaystyle h(x)=0$의 근의 갯수는 오직 하나이다. 
따라서 접점의 개수가 하나이므로 접선을 오직 하나 그을 수 있다.
점 $\displaystyle (p,~q)$이 연두색의 위치에 있을 때, 즉 $\displaystyle l(p)<q< g(p)$일 때는 극댓값이 양, 극솟값이 음이므로 $\displaystyle h(x)=0$의 근의 갯수는 서로 다른 세 개다.
따라서 접점의 개수가 세개이므로 접선을 세 개 그을 수 있다.
점 $\displaystyle (p,~q)$이 빨간색의 위치에 있을 때, 즉 $\displaystyle q< l(p),~q< g(p)$일 때는 극댓값과 극솟값이 모두 양이므로 $\displaystyle h(x)=0$의 근의 갯수는 오직 하나이다.
따라서 접점의 개수가 하나이므로 접선을 오직 하나 그을 수 있다.
점 $\displaystyle (p,~q)$가 $\displaystyle y=g(x)$,~점 $\displaystyle y=l(x)$에 있을 때는 극댓값 또는 극솟값이 점 $\displaystyle 0$이므로 $\displaystyle h(x)=0$의 근은 중근 하나와 실근 하나를 갖는다.
따라서 접점의 개수가 두개므로 접선을 두 개 그을 수 있다.
둘째, $\displaystyle p=0$일 때, $\displaystyle h'(t)=g'(t)- g''(t)t-g'(t)=-tg''(t) \leq 0$이므로 $\displaystyle h(t)$는 감소함수이므로 $\displaystyle h(t)=0$의 개수는 오직하나이다. 따라서 접선의 개수는 오직 하나이다.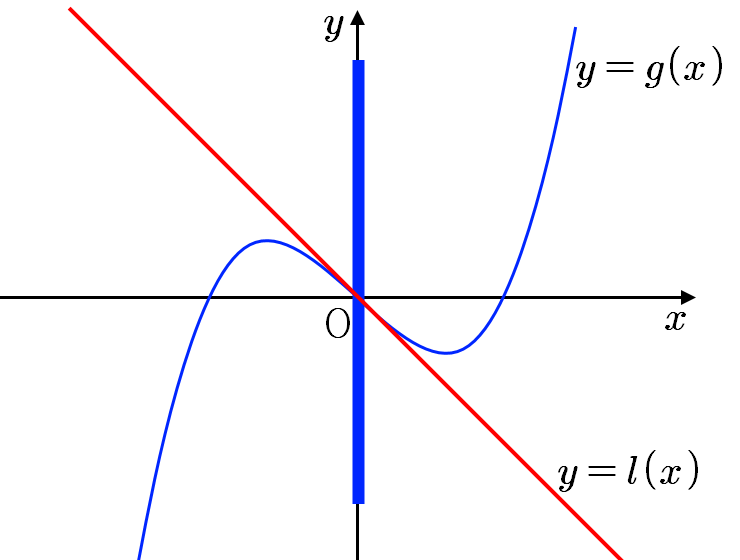

 
세째, $\displaystyle p<0$일 때, 삼차함수는 변곡점에 대칭이고 변곡점이 $\displaystyle (0,~0)$이므로 첫번째를 원점에 대칭하면 된다.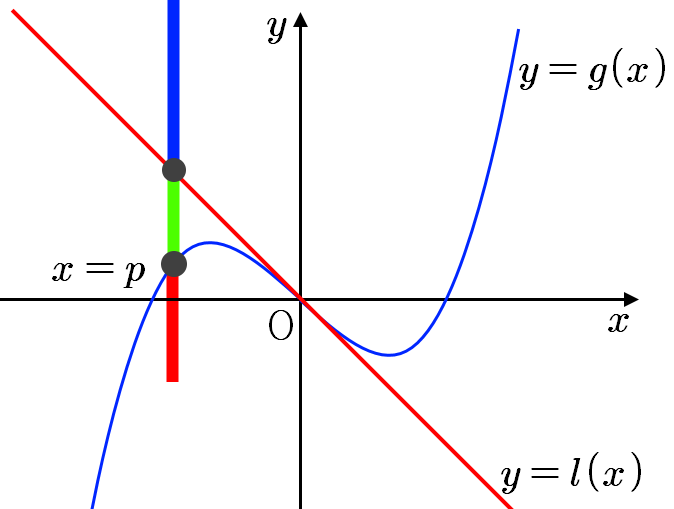 

이상에 변곡점이 원점일 때, 평면위의 점에서 곡선에 그은 접선의 개수를 구했다. 이것을 $\displaystyle x,~y$축으로 평행이동하면 맨 위의 그래프에서 보듯이 삼차함수에 그을 수 있는 접선의 개수를 구할 수 있다.
울산과고전문 더플러스수학학원 

https://naver.me/xb76xao4
 
과학고 내신대비와 대학입시를 위해서는 다음의 글을 참조하세요. 다양한 글이 있습니다.
과고1학년, 2학년 대신대비를 위해 더플러스수학학원의 구술시스템에서 실제로 하고 있는 문제를 보시려거나 과학고 3학년 AP미적분학을 준비하고자 하거나 대학교1학년 미적분학에 대해 공부하려고 하면 더플러스수학 프리미엄콘텐츠 를 이용해 보세요.

https://naver.me/FsR64KUy

과학고전문더플러스수학 : 네이버 프리미엄콘텐츠

더플러스수학 https://www.youtube.com/@THEPLUSMATH/channels
더플러스수학 블로그 https://plusthemath.tistory.com/
더플러스수학 네이버블로그 https://m.blog.naver.com/plusthemath