[수학의 기초] 평균값의 정리(1)

평균값의 정리에 대하여 알아보고 롤의 정리를 이용하여 평균값의 정리를 증명해 보자.

롤의 정리

함수 $\displaystyle f(x)$가 닫힌구간 $\displaystyle [a,~b]$에서 연속이고 열린구간 $\displaystyle (a,~b)$에서 미분가능할 때, $\displaystyle f(a)=f(b)$이면 

$\displaystyle f'(c)=0$

인 $\displaystyle c$가 열린구간 $\displaystyle (a,~b$에 적어도 하나 존재한다.

(증명)

함수 $\displaystyle f(x)$가 닫힌구간 $\displaystyle [a,~b]$에서 연속이므로 최대 최소의 정리 의 정리를 이용하여 증명한다.

먼저 함수$\displaystyle f(x)$가 열린구간 $\displaystyle (a,~b)$에 속하는 점 $\displaystyle c$에서 최댓값 또는 최솟값을 가질 때 와 그렇지 않을 때로 나누어서 증명하자.

(1) 열린구간 $\displaystyle (a,~b)$에 속하는 점 $\displaystyle c$에서 최댓값 또는 최솟값을 가질 때

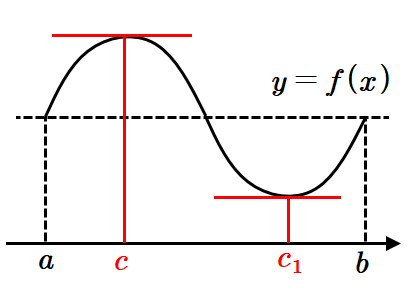
닫힌구간 $\displaystyle [a,~b]$에서 $\displaystyle f(c)$가 최댓값일 때,

$\displaystyle a \leq x \leq c$에서 $\displaystyle f(x) \leq f(c)$이므로

$\displaystyle f(x) - f(c) \leq 0$      $\displaystyle \frac{f(x) - f(c)}{x-c} \geq 0 ~~\cdots\cdots ~①$   

$\displaystyle x=c \in (a,~b)$에서 함수 $\displaystyle f(x)$는 미분가능하므로 ①의 양변에 극한 ( $\displaystyle   \lim\limits_{x \rightarrow c -}$ )를 취하면

$\displaystyle f'(c)=\lim\limits_{x \rightarrow c-}\frac{f(x) - f(c)}{x-c} \geq 0$

$\displaystyle c \leq x \leq b$에서 $\displaystyle f(x) \leq f(c)$이므로 위와 똑같이 하면

$\displaystyle f'(c)=\lim\limits_{x \rightarrow c-}\frac{f(x) - f(c)}{x-c} \leq 0$

따라서 $\displaystyle f'(c)=0$이다.

닫힌구간 $\displaystyle [a,~b]$에서 $\displaystyle f(c)$ 최솟값을 가질 때도 위와 같이 하면 $\displaystyle f'(c)=0$이다.

(2) 그렇지 않을 때 즉, (1)을 부정하면

$\displaystyle \sim \left( \right.$ 열린구간 $\displaystyle (a,~b)$에 속하는 점 $\displaystyle c$에서 최댓값 또는 최솟값을 가질 때  $\displaystyle   \left. \right)$

다른 말로 밑줄 친 부분은 다음과 같이 표현할 수 있다.

어떤 $\displaystyle c \in (a,~b)$가 존재하여 최댓값 또는 최솟값을 갖는다.

이것을 부정하면 "어떤"의 부정은 "모든", "임의의"이므로

임의의 $\displaystyle c \in (a,~b)$에 대하여 최댓값을 갖지 않고 최솟값도 갖지 않는다.

즉, 최댓값과 최솟값을 갖는 $\displaystyle x$는 $\displaystyle a$와 $\displaystyle b$이다. 그런데 $\displaystyle f(a)=f(b)$이므로 

함수 $\displaystyle f(x)$는 구간 $\displaystyle [a,~b]$에서 상수함수이다. 

따라서 구간 $\displaystyle (a,~b)$에 속하는 모든 점에서 미분하면 $\displaystyle 0$이므로 $\displaystyle f'(c)=0$인 $\displaystyle c \in (a,~b)$가 존재한다.