[수학의 기초] 함수의 극한의 엄밀한 정의(1) $\epsilon-\delta$, $\displaystyle p \rightarrow q$와 $\displaystyle \sim p ~or~ q$와 그 부정

과학고 AP 수업을 할 때, 극한이 $\displaystyle \epsilon-\delta$로 정의되는데 이 속에 조건 $\displaystyle p \rightarrow q$과 모든($\displaystyle \Large \forall$)과 어떤($\displaystyle \Large \exists$)등이 포함되어 있다. 즉,

극한의 엄밀한 정의

---

$\displaystyle \lim\limits_{x \rightarrow c} f(x)=L$ 

For all $\displaystyle \epsilon >0$, there exists some $\displaystyle \delta =\delta (\epsilon)$ such that for all $\displaystyle x$,

$\displaystyle 0<\left| x-c \right|<\delta ~~\Longrightarrow~~\left| f(x)-L \right| < \epsilon$

 

우리말로 쓰면 다음과 같이 표현할 수 있다.

임의의 $\displaystyle \epsilon >0$에 대하여 적당한 $\displaystyle \delta =\delta (\epsilon)$가 존재하여

$\displaystyle 0<\left| x-c \right|<\delta$을 만족하는 모든 $\displaystyle x$는 $\displaystyle\left| f(x)-L \right| < \epsilon$을 만족한다.

---

 

 

또, 이것의 부정 즉, $\displaystyle \lim\limits_{x \rightarrow c} f(x) \neq L$은

---

There exist some $\displaystyle \epsilon>0$ such that for every $\displaystyle \delta>0$, there exists $\displaystyle x_0$ which satisfies

$\displaystyle 0<\left| x_0-c \right|<\delta$ and $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$

우리말로 하면

적당한(어떤)  $\displaystyle \epsilon>0$를 잘 잡으면 모든 $\displaystyle \delta>0$에 대하여 적당한(어떤) $\displaystyle x_0$가 존재하여 $\displaystyle 0<\left| x_0-c \right|<\delta$ 이고 $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$이다.

직역을 하면

적당한(어떤)  $\displaystyle \epsilon>0$가 존재하여 $\displaystyle c$부근에서 아무리 $\displaystyle \delta > 0$를 잡아도 $\displaystyle 0<\left| x_0-c \right|<\delta$ 이고 $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$ 를 만족하는 $\displaystyle x_0$가 적어도 하나 존재한다.

---

 

위에서 보듯이

for all x,

$\displaystyle 0<\left| x-c \right|<\delta ~~\Longrightarrow~~\left| f(x)-L \right| < \epsilon$

에서 나타난 $\displaystyle p \rightarrow q$의 부정이

there exists $\displaystyle x_0$ which satisfies

$\displaystyle 0<\left| x_0-c \right|<\delta$ and $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$

으로 표현되는 이유에 관심을 가져보자.

즉, $\displaystyle p$ and $\displaystyle \sim q$

 

이제 수학 하 명제편에서

$\displaystyle p \longrightarrow q$

의 참 거짓을 확인해보자. 여기서 $\displaystyle p,~q$는 조건으로써 전체 집합 $\displaystyle U$에서 정의되고 진리집합이 각각 $\displaystyle P,~Q$라고 하자. 그러면

$\displaystyle P \subset Q$이면 $\displaystyle p \rightarrow q$가 참이고   $\displaystyle \cdots\cdots~①$

$\displaystyle P \not\subset Q$이면 $\displaystyle p \rightarrow q$가 거짓이다.  $\displaystyle \cdots\cdots~②$

먼저 ①의 $\displaystyle P \subset Q$에서 부분집합의 정의에는 다음의 명제가 포함되어 있다.

모든 $\displaystyle x \in U$에 대하여

$\displaystyle x \in P$이면 $\displaystyle x \in Q$    $\displaystyle \cdots\cdots~③$

즉, 위의 명제가 참이면  $\displaystyle P \subset Q$이다.

따라서 ①의 부정, 즉 ③을 부정하면

어떤 $\displaystyle x_0 \in U$에 대하여

$\displaystyle x_0 \in P$이고 $\displaystyle x_0 \not\in Q$    $\displaystyle \cdots\cdots~④$

즉 

$\displaystyle x_0 \in P$이고 $\displaystyle x_0 \not\in Q$

를 만족하는 $\displaystyle x_0 \in U$가 적어도 하나 존재한다. (물론 이 예를 우리는 반례-counterexample이라고 부른다.)

이것을 만족하면 우리는 $\displaystyle P \not\subset Q$이라 한다.

이제 이것을 집합의 포함관계와 드모르간의 법칙으로 정리해보자.

모든 $\displaystyle x  \in U$에 대하여 $\displaystyle  x \in p \rightarrow x \in q$ 

$\displaystyle \Longleftrightarrow$  $\displaystyle P \subset Q$ 

$\displaystyle \Longleftrightarrow$   $\displaystyle \sim \left\{ \right.$ $\displaystyle P \not\subset Q$이다. $\displaystyle \left.\right\}$   

$\displaystyle \Longleftrightarrow$ $\displaystyle \sim \left\{   x_0 \in P \right.$ 이고 $\displaystyle x_0  \not\in Q$를 만족하는 $\displaystyle x_0 \in U$가 존재한다. $\displaystyle \left.\right\}$

$\displaystyle \Longleftrightarrow$  모든 $\displaystyle x  \in U$에 대하여  $\displaystyle   x  \not\in P$ 이거나 $\displaystyle x \in Q$이다. 

$\displaystyle \Longleftrightarrow$  모든 $\displaystyle x  \in U$에 대하여  $\displaystyle   x   \in P^c$ 이거나 $\displaystyle x \in Q$이다. 

$\displaystyle \Longleftrightarrow$  모든 $\displaystyle x  \in U$에 대하여  $\displaystyle   x \in ( P^c \cup Q)$ 

$\displaystyle \Longleftrightarrow$  모든 $\displaystyle x  \in U$에 대하여  $\displaystyle   \sim p$ 또는 $\displaystyle q$이다.

 

이제  정수전체의 집합 $\displaystyle \mathbb{Z}$에서 명제 "$\displaystyle x$가 $\displaystyle 4$의 배수이면  $\displaystyle x$는 $\displaystyle 2$의 배수이다."을 가지고 이것이 "모든 $\displaystyle x \in \mathbb{Z}$에 대하여 $\displaystyle 4$의 배수가 아니거나 $\displaystyle 2$의 배수이다."와 동치(필요충분조건)를 위의 논리로 보여보자.

"$\displaystyle 4$의 배수이면  $\displaystyle 2$의 배수이다."

$\displaystyle \Longleftrightarrow$ "$\displaystyle 4$의 배수를 만족하는 모든 수는 $\displaystyle 2$의 배수이다."

$\displaystyle \Longleftrightarrow$  $\displaystyle \sim$ "어떤 $\displaystyle x_0 \in \mathbb{Z}$가 존재하여 $\displaystyle 4$의 배수이고  $\displaystyle 2$의 배수는 아니다."

$\displaystyle \Longleftrightarrow$   "모든 $\displaystyle x \in \mathbb{Z}$에 대하여 $\displaystyle 4$의 배수가 아니거나 $\displaystyle 2$의 배수이다."

 

정리하면 명제 $\displaystyle p \rightarrow q$는 $\displaystyle \sim p$ 또는 $\displaystyle q$와 동치이므로 명제 $\displaystyle p \rightarrow q$을 부정하면 $\displaystyle   p$ 그리고 $\displaystyle \sim q$이다.

물론 명제 $\displaystyle p \rightarrow q$에는 $\displaystyle p$를 만족하는 "모든"을 내포하고 있다. 또 그것의 부정인 "$\displaystyle   p$ 그리고 $\displaystyle \sim q$"에는 "어떤" 것이 존재하고 있다는 것을 포함하고 있다는 것에 주의하자.

$\displaystyle \Large{  \sim (p \rightarrow q) ~~\Longleftrightarrow ~p ~and ~\sim q }$

 

이제 구체적인 예를 가지고 극한값이 아님을 보이자.

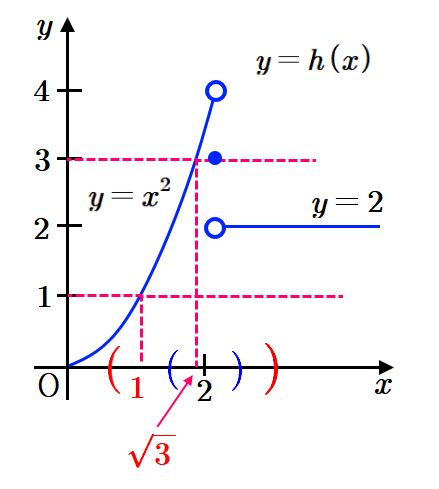
$\displaystyle h(x)=\begin{cases} x^2 &(0<x <2)\\3&(x=2) \\2&(>2)\end{cases}$에 대하여 $\displaystyle \lim\limits_{x \rightarrow 2} h(x) \neq 2$임을 보이자.

$\displaystyle \lim\limits_{x \rightarrow c} h(x) \neq L$은 다음과 같다. 

적당한(어떤)  $\displaystyle \epsilon>0$가 존재하여 $\displaystyle c$부근에서 아무리 $\displaystyle \delta > 0$를 잡아도 $\displaystyle 0<\left| x_0-c \right|<\delta$ 이고 $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$ 를 만족하는 $\displaystyle x_0$가 적어도 하나 존재한다.

여기서 핵심은 극한값 $\displaystyle L$을 중심으로 $\displaystyle \epsilon>0$을 어떻게 잡으며, 그에 따라 $\displaystyle 0<\left| x_0-c \right|<\delta$ 이고 $\displaystyle \left| f(x_0)-L \right| \geq \epsilon$을 만족하는 $\displaystyle x_0$가 $\displaystyle \delta>0$에 관계없이 존재함을 보이는 것이다.

예를 들어 위의 그림에서 극한값 $\displaystyle y=2$를 중심으로 $\displaystyle \epsilon$을 $\displaystyle1$로 하자. 이제 우리는 $\displaystyle \left|f(x_0)-2\right| \geq 1$ 즉,

$\displaystyle f(x_0)\leq 1,~f(x_0 )\geq3$    $\displaystyle \Longrightarrow$ $\displaystyle x_0 \leq 1$ 또는 $\displaystyle x_0 \geq \sqrt3$    $\displaystyle \cdots\cdots ~(\mathrm{i})$

을 만족하고 어떻게 $\displaystyle \delta>0$를 잡든 관계없이 

$\displaystyle 0<\left|x_0 -2\right|<\delta$   $\displaystyle \cdots\cdots ~(\mathrm{ii})$

를 만족하는 $\displaystyle x_0$를 잡을 수 있어야 한다.

그림을 보면 $\displaystyle \delta$를 어떻게 잡든 관계없이 $\displaystyle \sqrt3$보다 크고 $\displaystyle 2$보다 작은 실숫값은 항상 존재한다. 그 값을 $\displaystyle x_0$라 하면 $\displaystyle x_0$는 $\displaystyle (\mathrm{i})$, $\displaystyle  (\mathrm{ii})$를 동시에 만족하므로

$\displaystyle \lim\limits_{x \rightarrow 2} h(x) \neq 2$

이다.

$\displaystyle \delta$가 $\displaystyle  2-\sqrt3$보다 크면 $\displaystyle x_0$를 $\displaystyle 2-\sqrt3 <x_0<2$을 만족하는 $\displaystyle x_0$를 잡으면 되고

만약 $\displaystyle \delta$가 $\displaystyle  2-\sqrt3$보다 작으면 $\displaystyle x_0$를 $\displaystyle \left|x_0 -2\right|< \delta$를 만족하는 $\displaystyle2$보다 작은 $\displaystyle x_0$를 잡으면 된다.

ㅠㅠ