[2020년3월 가형 미적분 30번] [더플러스수학]

#2020년_3월_가형_모의고사_30번 #미적분킬러문항 문제에 대한 여러가지 풀이 입니다.

최고차항의 계수가 $\displaystyle 4$인 삼차함수 $\displaystyle f ( x)$와 실수 $\displaystyle t$에 대하여 함수 $\displaystyle g ( x)$를 

$\displaystyle g ( x)= \int _ {t} ^ {x} {f ( s)} ds$

라 하자. 상수 $\displaystyle a$에 대하여 두 함수 $\displaystyle f ( x)$와 $\displaystyle g ( x)$가 다음 조건을 만족시킨다.

---

(가) $\displaystyle f '  ( a)=0$

(나) 함수 $\displaystyle \left | g ( x)-g ( a) \right |$가 미분가능하지 않은 $\displaystyle x$의 개수는 $\displaystyle 1$이다.

---

실수 $\displaystyle t$에 대하여 $\displaystyle g ( a)$의 값을 $\displaystyle h ( t)$라 할 때, $\displaystyle h ( 3)=0$이고 함수 $\displaystyle h ( t)$는 $\displaystyle t=2$에서 최댓값 $\displaystyle 27$을 가진다. $\displaystyle f ( 5)$의 값을 구하시오. [4점]

 

 

https://youtu.be/qyXy-ucm-mw(풀이1)

https://youtu.be/bqNYjfLhEOY(풀이2)

 

 

 

(풀이3) 정답 432

[출제의도] 정적분으로 정의된 함수를 이용하여 문제를 해결한다.

$\displaystyle f ( x)$가 최고차항의 계수가 $\displaystyle 4$인 삼차함수이므로 

$\displaystyle g ( x)= \int _ {t} ^ {x} {} f ( s)ds$는 최고차항의 계수가 $\displaystyle 1$인 사차함수이고 실수 전체의 집합에서 함수 $\displaystyle g ( x)-g ( a)$는 미분가능하다. 

$\displaystyle g ( x) \geq g ( a)$일 때, $\displaystyle \left | g ( x)-g ( a) \right | =g ( x)-g ( a)$

$\displaystyle g ( x) < g ( a)$일 때, $\displaystyle \left | g ( x)-g ( a) \right | = - \left\{ g ( x)-g ( a) \right\}$

이므로 함수 $\displaystyle \left | g ( x)-g ( a) \right |$은 $\displaystyle g ( x)-g ( a) \neq 0$인 모든 $\displaystyle x$에서 미분가능하다.

$\displaystyle g ( x)-g ( a)=0$를 만족시키는 $\displaystyle x$의 값을 $\displaystyle k$라 하면,

$\displaystyle g ( k)=g ( a)$이므로 

$\displaystyle \frac {\left | g ( x)-g ( a) \right | - \left | g ( k)-g ( a) \right |} {x-k} = \frac {\left | g ( x)-g ( k) \right |} {x-k}$

(ⅰ) $\displaystyle x=k$의 좌우에서 $\displaystyle g ( x)-g ( a)$의 부호가 같을 때

$\displaystyle \lim\limits _ {x \rightarrow k-} {} \frac {\left | g ( x)-g ( k) \right |} {x-k} = \lim\limits _ {x \rightarrow k+} {} \frac {\left | g ( x)-g ( k) \right |} {x-k}$

이므로 함수 $\displaystyle \left | g ( x)-g ( a) \right |$는 $\displaystyle x=k$에서 미분가능하다.

(ⅱ) $\displaystyle x=k$의 좌우에서 $\displaystyle g ( x)-g ( a)$의 부호가 다르고 $\displaystyle f ( k)=0$일 때

$\displaystyle \lim\limits _ {x \rightarrow k-} {} \frac {\left | g ( x)-g ( k) \right |} {x-k} = \lim\limits _ {x \rightarrow k+} {} \frac {\left | g ( x)-g ( k) \right |} {x-k}$

이므로 함수 $\displaystyle \left | g ( x)-g ( a) \right |$는 $\displaystyle x=k$에서 미분가능하다.

(ⅲ) $\displaystyle x=k$의 좌우에서 $\displaystyle g ( x)-g ( a)$의 부호가 다르고 $\displaystyle f ( k) \neq 0$일 때,

$\displaystyle \lim\limits _ {x \rightarrow k-} {} \frac {\left | g ( x)-g ( a) \right |} {x-k} \neq \lim\limits _ {x \rightarrow k+} {} \frac {\left | g ( x)-g ( a) \right |} {x-k}$

이므로 함수 $\displaystyle \left | g ( x)-g ( a) \right |$는 $\displaystyle x=k$에서 미분가능하지 않다.

(나)에서 함수 $\displaystyle \left | g ( x)-g ( a) \right |$가 미분가능하지 않은 $\displaystyle x$의 개수가 $\displaystyle 1$이므로

$\displaystyle g ( x)-g ( a)=0$, $\displaystyle g '  ( x)=f ( x) \neq 0$

인 $\displaystyle x$가 단 하나 존재한다는 것을 알 수 있다.

그러므로 사차함수 $\displaystyle y=g ( x)$는 단 하나의 극솟값을 갖고 함수 $\displaystyle g ( x)$의 그래프와 직선 $\displaystyle y=g ( a)$는 서로 다른 두 점에서 만난다.

$\displaystyle g '  ( x)=0$인 방정식 $\displaystyle g ( x)-g ( a)=0$의 근을 $\displaystyle \alpha$, 함수 $\displaystyle g ( x)$가 극솟값을 가질 때의 $\displaystyle x$의 값을 $\displaystyle \beta$라 하면 $\displaystyle \alpha$, $\displaystyle \beta$의 대소관계에 따라 다음과 같이 두 경우로 나눌 수 있다.

(ⅰ) $\displaystyle \alpha < \beta$인 경우 (단, $\displaystyle g ( \gamma )=g ( \alpha )$, $\displaystyle \beta < \gamma$)

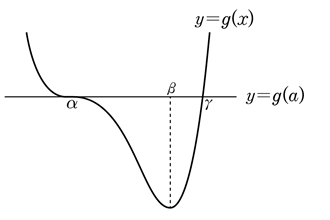
함수 $\displaystyle y=g ( x)$의 도함수 $\displaystyle y=f ( x)$의 그래프를 그려 보면

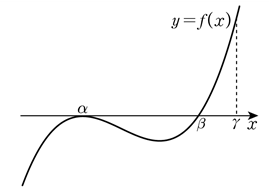
$\displaystyle g ( \alpha )=g ( \gamma )=g ( a)$이므로 $\displaystyle \alpha =a$ 또는 $\displaystyle \gamma =a$(가)에서 $\displaystyle f '  ( a)=0$이므로 $\displaystyle \alpha =a$이다.

따라서 $\displaystyle f ( x)=4 \left ( x-a \right ) ^ {2} \left ( x- \beta \right )$이다.

$\displaystyle h ( t)=g ( a)= \int _ {t} ^ {a} {f ( s)} ds$$\displaystyle = - \int _ {a} ^ {t} {} f ( s)ds$에서

$\displaystyle h '  ( t)= -f ( t)$함수 $\displaystyle h ( t)$가 $\displaystyle t=2$에서 최댓값, 즉 극댓값을 가지므로 $\displaystyle h '  ( 2)= -f ( 2)=0$

따라서 $\displaystyle a=2$ 또는 $\displaystyle \beta =2$이다.

$\displaystyle a=2$이면 $\displaystyle h ( 2)= \int _ {2} ^ {2} {f ( t)} dt=0 \neq 27$ 이므로 $\displaystyle a \neq 2$$\displaystyle \beta =2$이면

$\displaystyle h ( 3)= \int _ {3} ^ {a} {f ( s)} ds=0$이고,$\displaystyle h ( 2)= \int _ {2} ^ {a} {f ( s)} ds=27$이므로

$\displaystyle h ( 2)-h ( 3)= \int _ {2} ^ {3} {f ( s)} ds=27$이다.

$\displaystyle \begin{align} \int _ {2} ^ {3} {f ( s)} ds &= \int _ {2} ^ {3} {4 \left ( s-a \right ) ^ {2} \left ( s-2 \right )} ds \\&  = \int _ {2} ^ {3} {4 \left\{ s ^ {3} -2 \left ( a+1 \right ) s ^ {2} + \left ( a ^ {2} +4a \right ) s-2a ^ {2} \right\} } ds \\& = \left [ s ^ {4} - \frac {8} {3} \left ( a+1 \right ) s ^ {3} +2 \left ( a ^ {2} +4a \right ) s ^ {2} -8a ^ {2} s \right ] _ {2} ^ {3} \\&  =65- \frac {152} {3} \left ( a+1 \right ) +10 \left ( a ^ {2} +4a \right ) -8a ^ {2} \\&  =2a ^ {2} - \frac {32} {3} a+ \frac {43} {3}  =27 \end{align}$

이므로

$\displaystyle 3a ^ {2} -16a-19=0$

$\displaystyle \left ( a+1 \right ) \left ( 3a-19 \right ) =0$$\displaystyle a= -1$ 또는 $\displaystyle a= \frac {19} {3}$$\displaystyle a < 2$이므로

$\displaystyle a= -1$이다.

$\displaystyle f ( x)=4 \left ( x+1 \right ) ^ {2} \left ( x-2 \right )$라 하면 함수 $\displaystyle f ( x)$는 주어진 조건을 만족시킨다.

(ⅱ) $\displaystyle \alpha > \beta$인 경우 (단, $\displaystyle g ( \gamma )=g ( \alpha )$, $\displaystyle \gamma < \beta$)

함수 $\displaystyle y=g ( x)$의 도함수 $\displaystyle y=f ( x)$의 그래프를 그려 보면

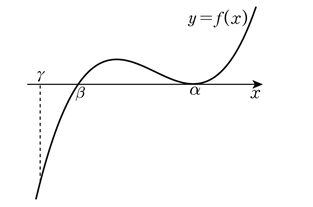
(가)에서 $\displaystyle f '  ( a)=0$이므로 $\displaystyle \alpha =a$이다.

따라서 $\displaystyle f ( x)=4 \left ( x-a \right ) ^ {2} \left ( x- \beta \right )$이다.$\displaystyle \alpha < \beta$인 경우와 마찬가지로 $\displaystyle \beta =2$이다.

$\displaystyle f ( x)=4 \left ( x-a \right ) ^ {2} \left ( x-2 \right )$$\displaystyle a \neq 3$이면 $\displaystyle h ( 3)= \int _ {3} ^ {a} {} f ( s)ds \neq 0$이므로 $\displaystyle a=3$

따라서 $\displaystyle f ( x)=4 \left ( x-3 \right ) ^ {2} \left ( x-2 \right )$이고

$\displaystyle h ( 2)$$\displaystyle = \int _ {2} ^ {a} {} f ( s)ds$$\displaystyle = \int _ {2} ^ {3} {} 4 \left ( s-3 \right ) ^ {2} \left ( s-2 \right ) ds$$\displaystyle = \frac {1} {3}$$\displaystyle h ( 2) \neq 27$이므로

주어진 조건을 만족시키는 함수 $\displaystyle f ( x)$가 존재하지 않는다.

따라서 $\displaystyle f ( x)=4 \left ( x+1 \right ) ^ {2} \left ( x-2 \right )$이다.

$\displaystyle f ( 5)=4 \times 36 \times 3=432$