[킬러문항] 2018학년도 가형 6월 30번 [더플러스수학]

실수 $ a $와 함수 $ f \left ( x \right ) =\ln \left ( x ^ {4} +1 \right ) -c $ ($ c>0 $인 상수)에 대하여 함수 $ g \left ( x \right ) $를

$$ g \left ( x \right ) = \int _ {a} ^ {x} {f \left ( t \right ) dt} $$

라 하자. 함수 $ y=g \left ( x \right ) $의 그래프가 $ x $축과 만나는 서로 다른 점의 개수가 $ 2 $가 되도록 하는 모든 $ a $의 값을 작은 수부터 크기순으로 나열하면 $ \alpha _ {1} ,~ \alpha _ {2} ,~ \cdots ,~ \alpha _ {m} $ ($ m $은 자연수)이다. $ a= \alpha _ {1} $일 때, 함수 $ g \left ( x \right ) $와 상수 $ k $는 다음 조건을 만족시킨다.

---

(가) 함수 $ g \left ( x \right ) $는 $ x=1 $에서 극솟값을 갖는다.

(나) $ \displaystyle  \int _ {\alpha _ {1} } ^ {\alpha _ {m} } {g \left ( x \right ) dx} =k \alpha _ {m} \int _ {0} ^ {1} {\left | f \left ( x \right ) \right | dx} $

---

$ mk \times e ^ {c} $의 값을 구하시오. [4점]

 

https://youtu.be/LlkLarDTwPM

 

 

 

정답 및 풀이를 보려면 아래를 클릭하세요.

 

정답 $16$

$ f \left ( x \right ) =\ln \left ( x ^ {4} +1 \right ) -C $, $ g ' \left ( x \right ) =f \left ( x \right ) $,

$\displaystyle f ' \left ( x \right ) = \frac {4x ^ {3} } {x ^ {4} +1} $

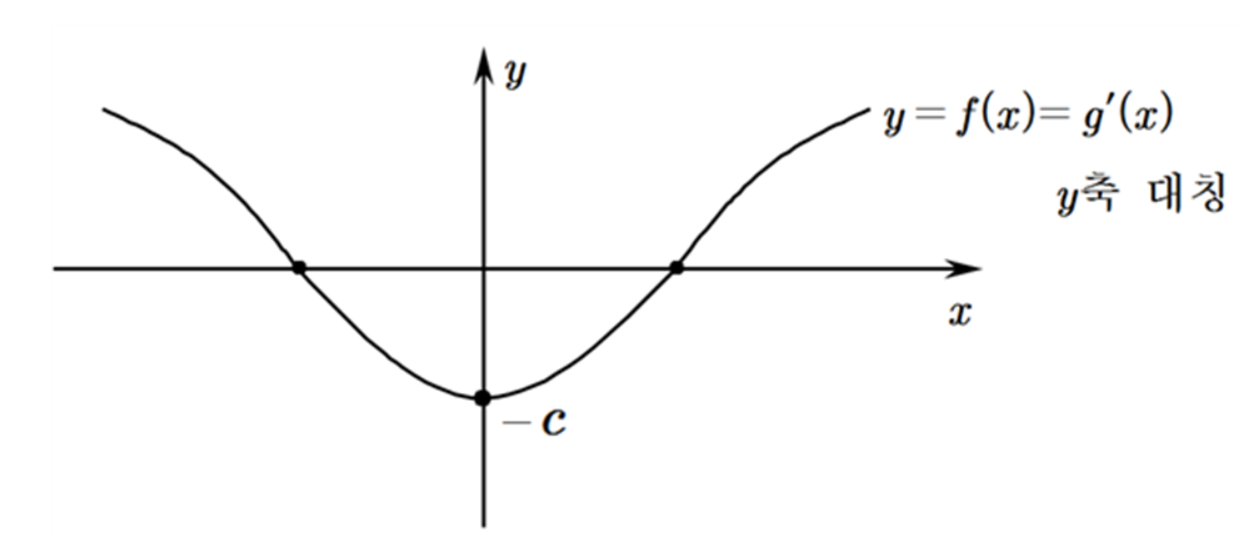
$ g \left ( x \right ) $는 $ x=1 $에서 극솟값을 가지므로

$ g ' ( 1)=f ( 1)=0 $

$ \ln 2-c=0 $

$ \therefore c=\ln 2 $

 

 

위의 그림에서 보듯이 $ y=f ( x) $는 $ y $축에 대칭인 함수이고 $ x=1 $에서 극솟값을 가지므로 $ y=f ( x) $가 $ x $축과 만나는 점은 $ ( \pm 1,~0) $이다. 이 때, $ \alpha _ {2} =-1,~ \alpha _ {3} =1 $이라 하자.

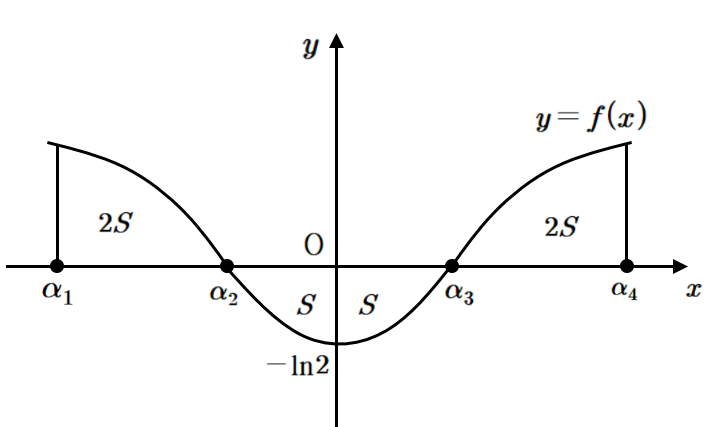
$\displaystyle g ( x)= \int _ {a} ^ {x} {} f ( x)dx=0 $인 점이 두 개만 있을 $ a $값을 구해보자. 먼저 $ g ( a)=0 $이므로 $ x=a $에서 $ g ( x) $가 $ 0 $이다. 또, $ x=0 $에서 $ x= \alpha _ {3} =1 $까지 $ f ( x) $와 $ x $축으로 둘러싸인 부분의 넓이를 $ S $라 하면, 즉 $ \displaystyle \int _ {0} ^ {1} {} f ( x)dx=-S $

그림에서 보듯이 $ x= \alpha _ {3} $에서 $ x $축의 양의 방향으로 $ f ( x) $와 $ x $축으로 둘러싸인 부분의 넓이가 $ 2S $인 점을 $ \alpha _ {4} $라 하고, $ x < -1 $인 점에서 $ x= \alpha _ {2} =-1 $까지 $ f ( x) $와 $ x $축으로 둘러싸인 부분의 넓이가 $ 2S $인 지점을 $ \alpha _ {1} $이라 하자.

그러면 $ \displaystyle g ( x)= \int _ {a} ^ {x} {} f ( x)dx=0 $를 만족하는 점이 두 개인 $ a $의 값은 $ \alpha _ {1} ,~ \alpha _ {2} ,~ \alpha _ {3} ,~ \alpha _ {4} $이다.

따라서 $ m=4 $이다. 또, $ f ( x) $가 $ y $축에 대칭이므로 $ \alpha _ {4} =- \alpha _ {1} $이다.

$ a= \alpha _ {1} $이라 두면 $ f ( x) $가 $ y $축에 대칭인 함수이므로 $ \displaystyle g ( x)= \int _ {\alpha _ {1} } ^ {x} {f ( t)dt} $는 $ \displaystyle g ( 0)= \int _ {\alpha _ {1} } ^ {0} {f ( x)dx} =2S+ ( -S)=S \neq 0 $이므로 원점에 대칭인 함수, 즉 기함수는 아니다. 그러나 $\displaystyle g ( x)=S+ \int _ {0} ^ {x} {f ( t)dt} $를 표현하면 여기서 $ \displaystyle h ( x)= \int _ {0} ^ {x} {} f ( t)dt $는 원점에 대칭인 함수이다. ($ \because $$ x $대신 $ -x $를 대입하고 $ f ( x) $가 $ f ( -x)=f ( x) $임을 이용하고 $ -t=s $로 치환하면 원점에 대칭임을 보일 수 있다.) ㅠㅠ 글로 표현하려하니 힘드네!!!

이제 $\displaystyle \int _ {\alpha _ {1} } ^ {\alpha _ {4} } {g \left ( x \right ) dx} $을 구해보자.

$ h ( x) $가 원점에 대칭인 함수이므로

$$ \int _ {\alpha _ {1} } ^ {\alpha _ {4} } {h \left ( x \right ) dx} = \int _ {\alpha _ {1} } ^ {- \alpha } {h ( x)dx=0} $$

이다. 또, $ \displaystyle S= \int _ {0} ^ {1} {} \left | f ( x) \right | dx $이다.

따라서

$\begin{align}  \int _ {\alpha _ {1} } ^ {\alpha _ {4} } g \left ( x \right ) dx &= \int _ {\alpha _ {1} } ^ {\alpha _ {4} }  S+h ( x) dx \\&= \int _ {\alpha _ {1} } ^ {- \alpha _ {1} }  S+h ( x)dx  =S ( - \alpha _ {1} - \alpha _ {1} )+0  \\&=-2S \alpha _ {1} =2 \alpha _ {4} \int _ {0} ^ {1}   |f ( x)|dx \end{align}$

$ \therefore k=2 $

$ \therefore mk \times e ^ {c} =4 \times 2 \times e ^ {\ln 2} =16 $