[평가원기출]2021학년도 9월 평가원 가형 21번-킬러문항[더플러스수학]

 

닫힌구간 $\displaystyle [-2 \pi ,~2 \pi ]$에서 정의된 두 함수

$$\displaystyle f ( x)=\sin kx+2 ,~ g ( x)=3\cos 12x$$

에 대하여 다음 조건을 만족시키는 자연수 $\displaystyle k$의 개수는? [$\displaystyle 4$점]

---

실수 $\displaystyle a$가 두 곡선 $\displaystyle y=f ( x)$, $\displaystyle y=g ( x)$의 교점의 $\displaystyle y$좌표이면  $$\displaystyle \left\{ \,x\,|\,f ( x)=a\, \right\} \subset \left\{ \,x\,|\, g ( x)=a\, \right\}$$ 이다.

---

① $\displaystyle 3$

② $\displaystyle 4$

③ $\displaystyle 5$

④ $\displaystyle 6$

⑤ $\displaystyle 7$

 

문제와 풀이 전부를 보시려면 다음 링크를.....https://plusthemath.tistory.com/395

https://youtu.be/YNo3MwDewCo(구독과 좋아요를...)

 

 

정답 및 풀이

자연수 $\displaystyle k$에 대하여 $\displaystyle f ( x)$의 주기는 $\displaystyle \frac {2 \pi } {k}$, $\displaystyle g ( x)$의 주기는 $\displaystyle \frac {2 \pi } {12} = \frac {\pi } {6}$이다.

만약 $\displaystyle k=12$일 때 그림을 그려보면

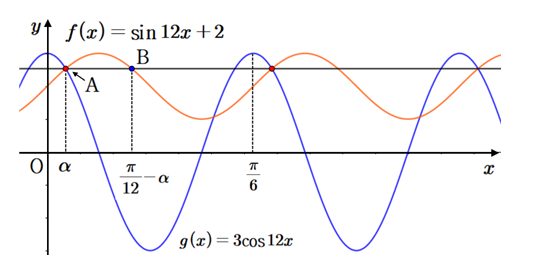
위의 그림에서 보듯이 점 $\displaystyle \mathrm { A}$와 다른 점 $\displaystyle \mathrm { B }$가 $\displaystyle f$와 $\displaystyle y=a$의 교점이 더 생기므로

$$\displaystyle \left\{ \,x \,|\,f ( x)=a \,\right\} \,\not\subset \,\left\{ \,x \, |\,g ( x)=a\, \right\}$$

마찬가지로 $\displaystyle k>12$일 때도 $\displaystyle g$의 한 주기인 $\displaystyle \frac {\pi } {6}$에서 $\displaystyle g ( x)=a$를 만족하지 않지만 $\displaystyle f ( x)=a$를 만족하는 $\displaystyle x$가 존재하므로 안 된다.

$\displaystyle k=6$일 때를 그려보면

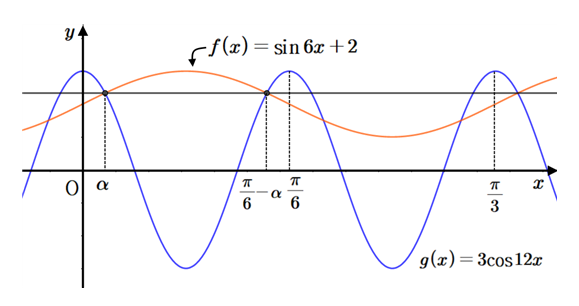
$\displaystyle y=a$와 $\displaystyle y=f ( x)$가 만나는 점은 모두 $\displaystyle y=a$와 $\displaystyle y=g ( x)$와 만나는 점이 되므로 $\displaystyle k=6$은 주어진 조건을 만족한다. 즉 $\displaystyle f ( x)=a$를 만족하는 근이 $\displaystyle \alpha$라 하면 $\displaystyle \frac {\pi } {6} - \alpha$도 근이므로 $\displaystyle g ( \alpha )=g \left ( \frac {\pi } {6} - \alpha \right )$를 만족해야 한다. 그런데 $\displaystyle 3\cos 12 \left ( \frac {\pi } {6} - \alpha \right ) =3\cos \left ( 2 \pi -12 \alpha \right ) =3\cos 12 \alpha$이므로 $\displaystyle \alpha \in \left\{ \,x\,|\,g ( x)=a \,\right\}$

마찬가지로 하면 $\displaystyle k=3$, $\displaystyle k=2$, $\displaystyle k=1$이면 된다.

이를 정리하면 자연수 $\displaystyle k$에 대하여 함수 $\displaystyle f ( x)$의 주기가 $\displaystyle \frac {2 \pi } {k}$이므로 $\displaystyle f ( x)=a$의 근을 $\displaystyle \alpha$라 하면 $\displaystyle f ( x)=a$의 다른 한 근은 $\displaystyle \frac {\pi } {k} - \alpha$도 근이다. 따라서 조건 $\displaystyle \left\{\,x\,|\,f ( x)=a \,\right\} \subset \left\{\, x\,|\,g ( x)=a \,\right\}$을 만족하려면 $\displaystyle x= \alpha ,~ \frac {\pi } {k} - \alpha$도 $\displaystyle g ( x)=a$의 근이어야 한다. 즉

$$\displaystyle g ( \alpha )=g \left ( \frac {\pi } {k} - \alpha \right ) ,~ 3\cos 12 \alpha =3\cos 12 \left ( \frac {\pi } {k} - \alpha \right )$$

$$\displaystyle 3\cos 12 \alpha =3\cos \left ( \frac {12 \pi } {k} -12 \alpha \right )$$

$$\displaystyle \therefore ~ \frac {12 \pi } {k} =2n \pi  ~( ~n 은 ~정수)$$

$$\displaystyle \therefore ~ 6=kn$$

따라서 $\displaystyle k$는 $\displaystyle 6$의 약수이므로 $\displaystyle 1,~2,~3,~6$인 $\displaystyle 4$가지이다.