[더플러스수학]2019년 울산과고2 심화수학 기출 20번 -gambler's ruin

 

$n$개의 동전을 가지고 있는 $A$와 무한한 동전을 가지고 있는 $B$가 서로 게임을 한다. 한 게임마다 각자 $1$개의 동전을 걸고 게임에서 이긴 사람이 모두 가진다. $A$가 한 게임에서 이길 확률은 $p$이며 $A$와 $B$가 같은 게임을 무한히 반복한다고 하자. 이 때, $A$가 모든 동전을 잃을 확률을 아래와 같음을 증명하시오.

$\displaystyle p \leq \frac{1}{2}$이면 $1$

$\displaystyle  p > \frac{1}{2}$이면 $\displaystyle \left( \frac{1-p}{p}\right)^n$

 

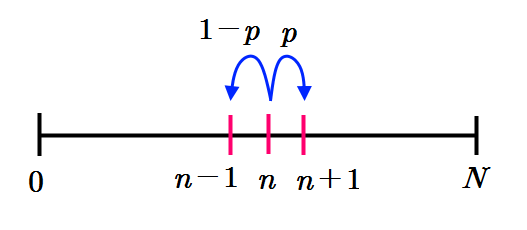
$P_n$을 $A$가 현재 $n$개의 동전을 가지고 게임에 참가하여 모든 동전을 잃을 확률이라 하자. 또, $B$가 무한개의 동전을 가지고 있는 것으로 하지 않고 $A$와 $B$ 두 사람이 가지고 있는 동전의 합을 $N$개라고 하자. 즉 $B$는 $N-n$개의 동전을 가지고 있다.

이렇게 가정하여 $P_n$을 구하고 $N \rightarrow \infty$하면 위의 결과를 얻을 수 있다.

이제 점화식을 만들자. $n$개의 동전을 가지고 동전을 모두 잃을 확률은

$(\mathrm{i})$ 첫번째 게임에서 동전을 잃는 경우

이 때 확률은 $1-p$이고 이 상황(동전의 개수:$n-1$개)에서 모든 동전을 잃을 확률 $P_{n-1}$이므로 확률은

$$\displaystyle (1-p)\times P_{n-1}$$

$(\mathrm{ii})$ 첫번째 게임에서 동전을 얻을 경우

이 때 확률은 $p$이고 이 상황(동전의 개수:$n+1$개)에서 모든 동전을 잃을 확률 $P_{n+1}$이므로 확률은

$$\displaystyle p\times P_{n+1}$$

두 사건은 배반서건이므로 $(\mathrm{i}),~(\mathrm{ii})$에 의해 $P_{n}$은

$$\displaystyle P_{n}= (1-p)\times P_{n-1}+p \times P_{n+1}~~\cdots\cdots ①$$

또 초기조건으로 $A$가 $0$개의 동전을 가지고 게임에 참가하면 게임을 할 수 없으므로 확률은 $P_0 =1$이다. 또, $A$가 $N$개의 동전을 가지고 게임에 참가하면 게임을 더이상 진행하지 않고 게임이 끝나므로 확률은 $P_N =0$이다.

①의 점화식을 풀자.

$$\displaystyle p P_{n+1}-P_{n}+(1-p)P_{n-1}=0$$

$$\displaystyle p (P_{n+1}-P_{n})=(1-p)(P_{n}-P_{n-1})$$

$$\displaystyle P_{n+1}-P_{n}=\frac{1-p}{p}(P_{n}-P_{n-1})$$

$$\begin{align} \therefore~ P_{n} &= P_0 + \sum_{i=1}^{n} (P_1 -P_0 )\left(\frac{1-p}{p}\right)^{i-1} \\&= P_0 + \frac{(P_1 -P_0)\left\{1-\left(\frac{1-p}{p}\right)^n \right\}}{1-\frac{1-p}{p}}\\&= 1 + \frac{(P_1 -1)\left\{1-\left(\frac{1-p}{p}\right)^n \right\}}{1-\frac{1-p}{p}} ~~\cdots\cdots ② \end{align}$$

한편 $P_N =0$이므로 ②에 $n=N$을 대입하면

$$\begin{align} 0=P_{N} = 1 + \frac{(P_1 -1)\left\{1-\left(\frac{1-p}{p}\right)^N \right\}}{1-\frac{1-p}{p}} \end{align}$$

$$-1+\frac{1-p}{p} = (P_1 -1)\left\{1-\left(\frac{1-p}{p}\right)^N \right\}$$

$$\therefore ~\frac{-1+\frac{1-p}{p}}{ 1-\left(\frac{1-p}{p}\right)^N  } = P_1 -1 ~~\cdots\cdots~③$$

③을 ②에 대입하여 정리하면

$$\therefore~ P_{n} =  1 - \frac{1-\left(\frac{1-p}{p}\right)^n }{ 1-\left(\frac{1-p}{p}\right)^N}$$

여기서 $\frac{1-p}{p}>1$일 때, 즉 $p <\frac{1}{2}$일 때, $\lim\limits_{N \rightarrow \infty} \left( \frac{1-p}{p}\right)^N =\infty$이므로 

$$\lim\limits_{N \rightarrow \infty}P_n =1$$

또, $\frac{1-p}{p}<1$일 때, 즉 $p >\frac{1}{2}$일 때, $\lim\limits_{N \rightarrow \infty} \left( \frac{1-p}{p}\right)^N =0$이므로 

$$\lim\limits_{N \rightarrow \infty}P_n = \left( \frac{1-p}{p}\right)^n$$

$p=\frac{1}{2}$일 때, ①에서 $p=\frac{1}{2}$을 대입하면

$$\displaystyle P_{n}= \frac{  P_{n-1}+ \times P_{n+1}}{2}$$

수열 $\left\{ P_n \right\}$은 등차수열이고 $P_0 =1,~P_N=0$이므로

$$P_n = 1+ n \times \left(\frac{-1}{N}\right)$$

따라서

$$\lim\limits_{N \rightarrow \infty}P_n = 1$$

이를 모두 정리하면

$\displaystyle p \leq \frac{1}{2}$이면 $1$

$\displaystyle  p > \frac{1}{2}$이면 $\displaystyle \left( \frac{1-p}{p}\right)^n$