[옥동수학학원][울산과고기출] 에르미트 항등식과 그 증명방법들(1)[더플러스수학]

이 글에는 에르미트 항등식에 대한 증명을 하려고 한다. 울산 옥동에 있는 울산과고전문 수학학원 더플러스수학학원입니다. 울산과고 기출문제 중에 하나입니다. 2017년 1학년 1학기 중간고사에 나왔다. 
$$\displaystyle \left [ x \right ] + \left [ x+ \frac {1} {n} \right ] + \left [ x+ \frac {2} {n} \right ] + \cdots + \left [ x+ \frac {n-1} {n} \right ] = \left [ nx \right ]$$ 임을 보이시오. (단, $\displaystyle [x]$ 는 $\displaystyle x$ 를 넘지 않는 가장 큰 정수이다.)[6점]  [2017 과고1 1학기 중간 주11]
위의 항등식을 샤를 에르미트가 만든 항등식으로 그 이름을 따서 '에르미트 항등식'이라고 한다.
https://youtu.be/nAyjopeVhAU(구독과 좋아요!!)

크게 두가지 방법으로 증명하는데

(i) 가우스기호-바닥함수의 성질을 이용한 증명방법

 

(ii) 주기함수임을 보이는 대수적-해석적 증명방법

 

이 있다. 어제 울산예비과고생들과 2017년 학교 기출문제를 풀이하는 과정에서 첫번째 방법은 원장인 내가, 두번째 방법은 곽샘이 증명했다. 그 내용을 정리해보기로 한다.

 

(i) 가우스기호($\displaystyle \mathrm{ \large {[~]}}$)-바닥함수(floor integer function $\displaystyle \mathrm{\large{\lfloor ~ \rfloor}}$)의 성질을 이용한 방법

*여기서는 바닥함수 기호를 쓰지 않고 가우스기호를 사용하여 증명한다.
먼저 일반화하지 않고 $\displaystyle n=4$일 때를 보이고 이를 이용하여 일반화하자. 그 과정이 학생들이 이해하기가 좀 더 쉽다. 즉
$$\displaystyle \left [ x \right ] + \left [ x+ \frac {1} {4} \right ] + \left [ x+ \frac {2} {4} \right ] +  \left [ x+ \frac {3} {4} \right ] = \left [ 4x \right ] ~\cdots\cdots~(\mathrm{i})$$  
위의 항등식을 증명하기 위해 먼저 $\displaystyle x=m+\alpha$ ($\displaystyle m$은 정수, $\displaystyle 0 \leq \alpha <1$)로 두자. 그러면 소수부분 $\displaystyle \alpha$에 $\displaystyle 0,~\frac{1}{4},~\frac{2}{4}, ~\frac{3}{4}$를 더하여 가우스기호를 취하기 때문에 $\displaystyle \alpha$의 범위를 $$\displaystyle 0\leq \alpha< \frac{1}{4}, ~ \frac{1}{4} \leq \alpha < \frac{2}{4},~\frac{2}{4} \leq \alpha < \frac{3}{4},~\frac{3}{4} \leq \alpha< 1$$ 로 나누어서 증명한다.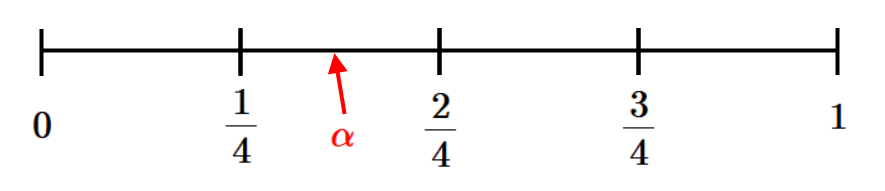

예를 들어 위의 그림에서 보듯이 $\displaystyle  \frac{1}{4} \leq \alpha < \frac{2}{4}$에 있다고 하면, 이 $\displaystyle \alpha$에 $\displaystyle 0,~\frac{1}{4}, ~ \frac{2}{4},~\frac{3}{4}$를 더하여 소수부분이 $\displaystyle 1$를 넘는 경우는 $\displaystyle \frac{3}{4}$를 더한 경우로 $\displaystyle 1$개 존재한다. 따라서
$$\displaystyle \left [ x \right ] =m,~\left [ x+ \frac {1} {4} \right ]=m,~ \left [ x+ \frac {2} {4} \right ]=m,~  \left [ x+ \frac {3} {4} \right ] =\textcolor{red}{m+1}$$
이므로 $\displaystyle(\mathrm{i})$의 좌변은 $\displaystyle 3m+(m+1)=4m+1$이다.
우변에 있는 $\displaystyle 4x$의 범위는 $\displaystyle m + \frac{1}{4} \leq x <m+ \frac{2}{4}$이므로 $$\displaystyle 4m+1\leq 4x<4m+2$$
이다. 그러므로 $\displaystyle(\mathrm{i})$의 우변 $\displaystyle \left[ 4x \right]$는 $$\displaystyle \left[4x \right]=\textcolor {red}{4m+1}$$
따라서 $\displaystyle  \frac{1}{4} \leq \alpha < \frac{2}{4}$일 때 $\displaystyle(\mathrm{i})$이 증명되었다.
$\displaystyle  \alpha$가 $\displaystyle  0 \leq \alpha < \frac{1}{4}$, $\displaystyle  \frac{2}{4} \leq \alpha < \frac{3}{4}$, $\displaystyle  \frac{3}{4} \leq \alpha < 1$일 때도 동일하게 증명된다.
이 과정을 일반화하여 서술해보면 다음과 같다. 
$\displaystyle  \frac{i}{4} \leq \alpha < \frac{i+1}{4}~(i=0,~1,~2,~3)$일  때, $\displaystyle \alpha$에 $\displaystyle 0,~\frac{1}{4}, ~ \frac{2}{4},~\frac{3}{4}$를 더하여 소수부분이 $\displaystyle 1$를 넘는 경우는 $\displaystyle \frac{4-i}{4}$에서 $\displaystyle \frac{4-1}{4}$까지를 더한 경우로 $\displaystyle (4-1)-(4-i)+1=\textcolor {red}{i}$개 존재한다. 따라서 좌변은 
$$\displaystyle (m+1)\times (\textcolor{red}{i})+m(\textcolor {red}{4-i})= \textcolor{red}{4m+i}$$
이다.
우변에 있는 $\displaystyle 4x$의 범위는 $\displaystyle m + \frac{\textcolor{red}{i}}{4} \leq x <m+ \frac{\textcolor {red}{i+1}}{4}$이므로  $$\displaystyle 4m+\textcolor{red}{i}\leq 4x<4m+\textcolor {red}{i+1}$$
이다. 그러므로 $\displaystyle(\mathrm{i})$의 우변 $\displaystyle \left[ 4x \right]$는  $$\displaystyle \left[4x \right]=\textcolor {red}{4m+i}$$
따라서 증명되었다. 
위에서 $\displaystyle n=4$일 때 증명했다면 이제 $\displaystyle n$으로 일반화하자.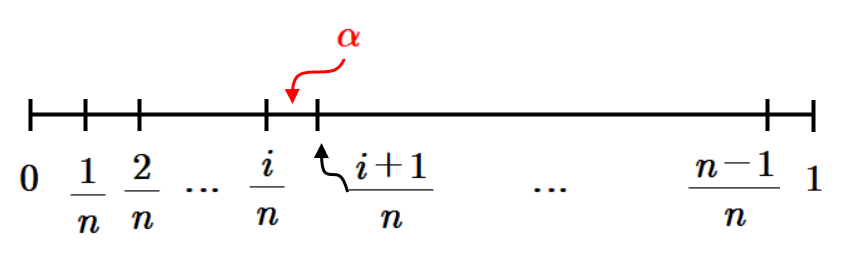

먼저 $\displaystyle x=m+\alpha$ ($\displaystyle m$은 정수, $\displaystyle 0 \leq \alpha <1$)로 두자. 그러면 소수부분 $\displaystyle \alpha$에 $\displaystyle  \frac{i}{n}$ ($\displaystyle i=0,~1,~2,~\cdots,~(n-1)$)를 더하여 가우스기호를 취하기 때문에 $\displaystyle i=0,~1,~2,~\cdots,~(n-1)$인 $\displaystyle i$에 대하여 $\displaystyle \alpha$의 범위를  $$\displaystyle \frac{i}{n} \leq \alpha< \frac{i+1}{n}$$ 로 나누어서 증명하자.
$\displaystyle  \frac{i}{n} \leq \alpha < \frac{i+1}{n}~(i=0,~1,~2,~\cdots,~n-1)$일  때, $\displaystyle \alpha$에 $\displaystyle 0,~\frac{1}{n}, ~ \frac{2}{n},~\cdots ,~\frac{n-1}{n}$를 더하여 소수부분이 $\displaystyle 1$를 넘는 경우는 $\displaystyle \frac{n-i}{n}$에서 $\displaystyle \frac{n-1}{4}$까지를 더한 경우로 $\displaystyle (n-1)-(n-i)+1=\textcolor {red}{i}$개 존재한다. 따라서 좌변은 
$$\displaystyle (m+1)\times (\textcolor{red}{i})+m(\textcolor {red}{n-i})= \textcolor{red}{nm+i}$$
이다.
우변에 있는 $\displaystyle 4x$의 범위는 $\displaystyle m + \frac{\textcolor{red}{i}}{n} \leq x <m+ \frac{\textcolor {red}{i+1}}{n}$이므로  $$\displaystyle n m+\textcolor{red}{i}\leq nx<nm+\textcolor {red}{i+1}$$
이다. 그러므로 $\displaystyle(\mathrm{i})$의 우변 $\displaystyle \left[ nx \right]$는  $$\displaystyle \left[nx \right]=\textcolor {red}{nm+i}$$
따라서 증명되었다. 
다음에는 주기함수의 성질을 이용하여 증명해보자.
2020/12/31 - [분류 전체보기] - [울산과고기출] 에르미트 항등식과 그 증명방법들(2)[더플러스수학]


과고1학년, 2학년 대신대비를 위해 더플러스수학학원의 구술시스템에서 실제로 하고 있는 문제를 보시려거나 과학고 3학년 AP미적분학을 준비하고자 하거나 대학교1학년 미적분학에 대해 공부하려고 하면 더플러스수학 프리미엄콘텐츠 를 이용해 보세요.

https://naver.me/FsR64KUy

과학고전문더플러스수학 : 네이버 프리미엄콘텐츠