[수학의 기초] 카발리에리의 원리-정적분의 활용

https://youtu.be/FnwgXBIVTOA(구독과 좋아요)

카발리에리의 원리(Cavalieri's Principle)

같은 높이를 갖는 입체들이 각 높이에서 동일한 넓이를 가진다면 똑같은 부피를 갖는다.

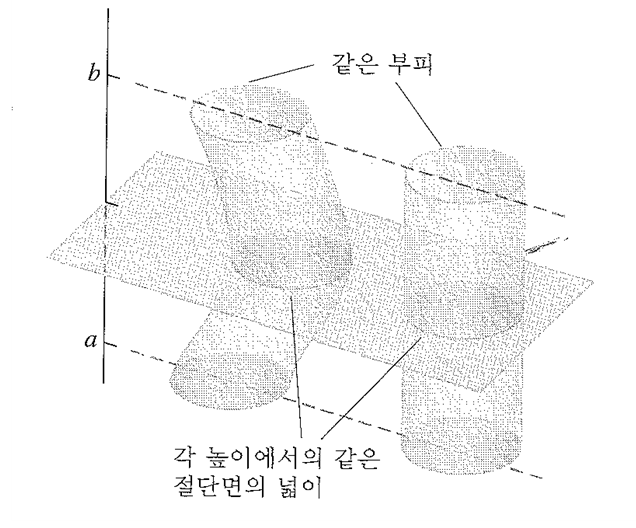
절단면의 넓이함수 $\displaystyle A ( x)$와 구간 $\displaystyle [a,~b]$가 두 입체들에 대해서 똑같은 조건이기 때문에 이 원리는 부피의 정의로부터 두 입체의 부피가 명백히 같다는 것을 말한다.

 

---

다음 문제를 읽고 물음에 답하여라.(카발리에리의 원리)

(1) 곡선으로 둘러싸인 높이가 같은 두 개의 도형 $\displaystyle \mathrm {M,~N}$이 있다. 일정한 직선 $\displaystyle \mathrm {XY}$에 평행인 직선을 그렸을 때 $\displaystyle \mathrm M$의 내부에 있는 부분의 길이와 $\displaystyle \mathrm N$의 내부에 있는 부분의 길이의 비가 항상 $\displaystyle m:n$이라고 한다. $\displaystyle \mathrm M$과 $\displaystyle \mathrm N$의 넓이 사이에는 어떤 관계가 있는지 설명하여라.

(2) 문제 (1)의 결과를 이용하여 타원 $\displaystyle \frac {x ^ {2} } {a ^ {2} } + \frac {y ^ {2} } {b ^ {2} } =1$(단, $\displaystyle a>b>0$)의 넓이를 구하여라.

(3) 그림과 같이 반지를 $\displaystyle r$인 두 개의 통나무로 된 원기둥이 축이 직교하면서 교차한다. 두 원기둥의 공통 부분의 부피를 문제 (1)의 결과를 이용하여 구하려고 한다. 그 방법을 설명하여라.

---

 

 

---

[2012학년도 아주대 논술 예시문제]

※ 다음 그림을 참조하여 [문제 1-3,4]에 답하라.

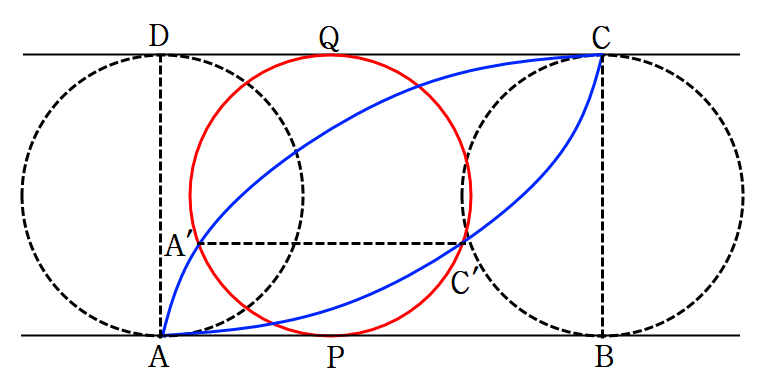
위 그림에서, 곡선$\displaystyle \mathrm{AA ' C}$ 는 $\displaystyle \mathrm A$에서 접하고 있던 반지름 $\displaystyle r$인 원이 선분 $\displaystyle {\overline {\mathrm{AB}} }$ 를 따라 $\displaystyle \mathrm B$까지 굴러갈 때 원 위의 점 $\displaystyle \mathrm A$가 그린 싸이클로이드 곡선이고, 곡선 $\displaystyle \mathrm{CC ' A }$는 $\displaystyle \mathrm C$에서 접하고 있던 반지름 $\displaystyle r$인 원이 선분 $\displaystyle {\overline {\mathrm{CD}} }$를 따라 $\displaystyle \mathrm D$까지 굴러갈 때 원 위의 점 $\displaystyle \mathrm C$가 그린 싸이클로이드 곡선이다. 단, $\displaystyle {\overline {\mathrm{AD}} }$와 $\displaystyle {\overline {\mathrm{BC}} }$는 이 원들의 지름이고, $\displaystyle \mathrm{A '}$과 $\displaystyle \mathrm{C '}$은 그림과 같이 $\displaystyle \mathrm{P}$와 $\displaystyle \mathrm{Q}$에 동시에 접하는 반지름 $\displaystyle r$인 원 위에 있다.

[문제 1-3] (15점) 선분 $\displaystyle \mathrm{ A ' C '}$이 선분 $\displaystyle \mathrm{AB}$에 평행함을 보여라.

 

[문제 1-4] (10점) 카발리에리의 원리와 [문제 1-3]의 결과를 이용하여 싸이클로이드 곡선 $\displaystyle \mathrm{AA ' C}$와 선분 $\displaystyle \mathrm{AB}$ 그리고 원의 지름 $\displaystyle \mathrm{BC}$로 둘러싸인 영역의 넓이를 구하라.

---