[수학의 기초] [정적분의 정의] 2008학년도 연세대 모의논술 [더플러스수학]

2008학년도 연세대 모의논술 문제를 통해 정적분의 정의를 이용하여 곡선의 길이를 구하는 공식을 여러가지 방식으로 유도해 본다.

youtu.be/QuhLNX7rK4A(구독과 좋아요)

2008학년도 연세대 모의논술

제시문을 읽고 물음에 답하시오. (40점)

함수 $\displaystyle f ( x) $의 도함수 $\displaystyle f ' ( x) $가 닫힌구간 $\displaystyle \left [ a,~b \right ] $에서 연속이고, $\displaystyle y=f ( x) $의 그래프가 [그림 1]과 같을 때, 다음 물음에 답하시오.

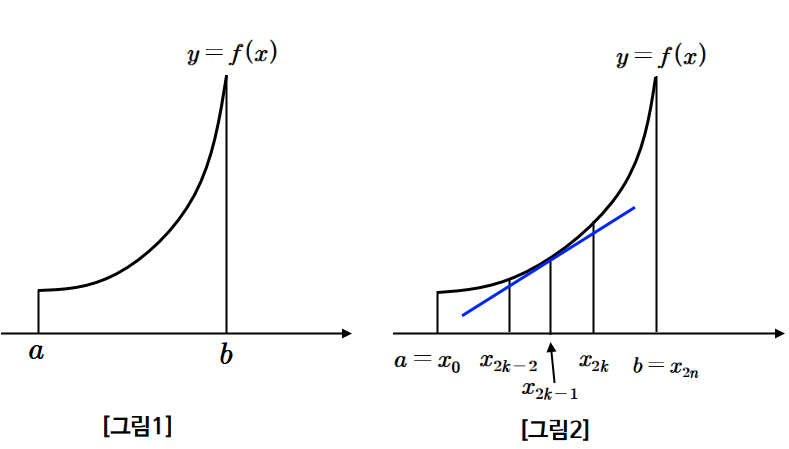
[문제 1-1] 곡선 $\displaystyle y=f ( x) $ 위의 점 $\displaystyle ( a,~f ( a)) $부터 점 $\displaystyle ( b,~f ( b)) $까지의 곡선의 길이를 정적분의 정의를 이용하여 구하시오. (10점)

 

[문제 1-2] [그림 2]는 [그림 1]의 닫힌구간 $\displaystyle \left [ a,~b \right ] $를 $\displaystyle 2n $개의 균등한 소구간으로 나눈 그래프이다. 이때, 점 $\displaystyle ( x _ {2k-1} ,~f ( x _ {2k-1} )) $에서의 접선의 식을 $\displaystyle y=g _ {k} ( x) $이라고 하자.  접선 위의 점 $\displaystyle ( x _ {2k-2} ,~g ( x _ {2k-2} )) $와 점 $\displaystyle ( x _ {2k} ,~g ( x _ {2k} )) $사이의 거리를 $\displaystyle l _ {k} $라고 할때, $$\displaystyle \lim\limits _ {n \rightarrow \infty } {\sum\limits _ {k=1} ^ {n} l _ {k} } $$의 값을 구하시오. (20점)

 

[문제 1-3] 위의 [1-1]과 [1-2]의 결과를 비교분석하고, [1-1]과 같은 결론을 유도할 수 있는 다른 방법에 대하여 논하시오. (10점)