2021학년도 연세대 수리논술 자연2

[문제 1] 한 개의 주사위를 $\displaystyle 3$번 던져 나온 눈의 수를 차례로 $\displaystyle a,~b,~c$라 하자. 이차방정식 $\displaystyle x^2 +y^2 +ax+by+6=0$이 원을 나타낼 때, 방정식 $\displaystyle x+2y+c=0$이 나타내는 직선이 이 원의 넓이를 이등분할 확률을 구하시오. [10점]

 

 

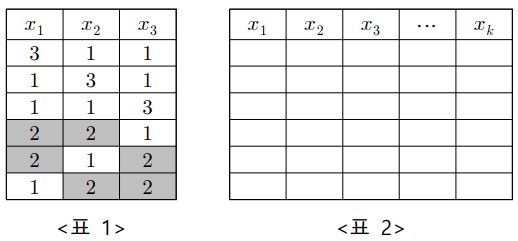
[문제 2] 방정식 $\displaystyle x_1 +x_2 +x_3 = 5$를 만족시키는 양의 정수해를 <표 1>과 같이 나타냈을 때, 숫자 $\displaystyle 2$가 나오는 횟 수는 $\displaystyle 6$이다. 자연수 $\displaystyle n$에 대하여 방정식 $\displaystyle x_1 +x_2 +x_3 +\cdots +x_k = n$을 만족시키는 양의 정수해를 <표 2>와 같이 나열하였을 때, 자연수 $\displaystyle r$ ($\displaystyle 1 \leq r \leq n-k+1$)가 나오는 횟수를 $\displaystyle n,~k,~r$를 이용하여 나타내시오. (단, $\displaystyle k$는 $\displaystyle 2 \leq k \leq n$인 자연수이다.) [12점]

 

 

 

[제시문] 어떤 삼각형 $\displaystyle \mathrm{ABC}$가 있을 때, 사각형 $\displaystyle \mathrm{PQRS}$가 직사각형이 되도록 삼각형 $\displaystyle \mathrm{ABC}$의 세 변 위의 네 점 $\displaystyle \mathrm{P,~Q,~R,~S}$를 선택한다. 다음 물음에 답하시오.

[문제 3-1] 사각형 PQRS의 넓이가 최대일 때, 삼각형 $\displaystyle \mathrm{ABC}$의 넓이와 사각형 $\displaystyle \mathrm{PQRS}$의 넓이의 차가 $\displaystyle 43$이라 하자. 이 때, 삼각형 $\displaystyle \mathrm{ABC}$의 넓이를 구하시오. [5점]

[문제 3-2] 사각형 $\displaystyle \mathrm{P'Q'R'S'}$이 다음 조건을 만족시킬 때, 삼각형 $\displaystyle \mathrm{ABC}$의 넓이를 구하시오. [15점]

(가) 사각형 $\displaystyle \mathrm{P'Q'R'S'}$은 직사각형이고 네 꼭짓점은 삼각형 $\displaystyle \mathrm{ABC}$와 사각형 $\displaystyle \mathrm{PQRS}$의 변 위에 있다. 그리고 두 사각형 $\displaystyle \mathrm{PQRS}$와 $\displaystyle \mathrm{P'Q'R'S'}$의 내부가 서로 겹치는 부분은 없다.

(나) 두 사각형 $\displaystyle \mathrm{PQRS}$와 $\displaystyle \mathrm{P'Q'R'S'}$의 넓이의 합이 최대일 때, 삼각형 $\displaystyle \mathrm{ABC}$의 넓이에서 두 사각형 $\displaystyle \mathrm{PQRS}$와 $\displaystyle \mathrm{P'Q'R'S'}$의 넓이의 합을 뺀 값은 $\displaystyle 47$이다.

 

 

 

[제시문] 좌표평면에서 네 직선 $\displaystyle x= -\frac{1}{3},~x+y=2,~y= \frac{1}{5},~y= \frac{4}{3}$로 이루어지는 사각형을 $\displaystyle D$라 하자. 자연수 $\displaystyle n$에 대하여, 네 변이 좌표축에 평행한 정사각형 중에서 한 변의 길이가 $\displaystyle \frac{1}{2^n }$이고 각 꼭짓점의 $\displaystyle x$좌표와 $\displaystyle y$좌표에 $\displaystyle 2^n$을 곱하여 각각 정수가 되는 정사각형들의 모임을 집합 $\displaystyle S_n$이라 하자. 다음 물음에 답하시오.

[문제 4-1] $\displaystyle S_n$의 원소 중에서 사각형 $\displaystyle D$의 둘레 및 내부에 포함되는 모든 정사각형의 개수를 $\displaystyle f(n)$이라 하고, 실수 $\displaystyle \alpha$에 대하여 수열 $\displaystyle \left\{ b_n \right\}$을 $\displaystyle b_n = \alpha n +\ln f(n)$이라 하자. 수열 $\displaystyle \left\{ b_n \right\}$이 수렴하도록 하는 $\displaystyle \alpha$의 값을 구하고, 이때 극한값 $\displaystyle \lim\limits _{n  \rightarrow \infty} b_n$을 구하시오. [8점]

[문제 4-2] $\displaystyle S_n$의 원소 중에서 사각형 $\displaystyle D$의 둘레와 두 점 이상에서 만나는 모든 정사각형의 개수를 $\displaystyle g(n)$이라 하고, 실수 $\displaystyle \beta$에 대하여 수열 $\displaystyle \left\{ c_n \right\}$을 $\displaystyle c_n = \beta n +\ln g(n)$이라 하자. 수열 $\displaystyle \left\{ c_n \right\}$이 수렴하도록 하는 $\displaystyle \beta$의 값을 구하고, 이때 극한값 $\displaystyle \lim\limits _{n  \rightarrow \infty} c_n$을 구하시오. [10점]