[수학의 기초] 일대일 대응인 연속함수는 그 역함수도 연속함수이다.

과학고 AP-Calculus수업에서 다음 명제와 부딪혔다. 이것을 증명해 보자.

정리  열린 구간 \(\displaystyle  (a,~b)\)에서 정의된 일대일 대응인 연속함수 \(\displaystyle f\)를 생각하자. 그러면 함수 \(\displaystyle f\)의 역함수인 \(\displaystyle f^{-1} \)도 연속함수이다.

 

위의 명제를 증명하기 위해서는 먼저 다음의 보조정리를 증명한다.

열린 구간 \(\displaystyle  (a,~b)\)에서 정의된 일대일 대응인 연속함수 \(\displaystyle  f\)는 그 구간에서 증가함수이거나 감소함수이다.

 

(증명) 귀류법으로 증명하자. 만약 함수 \(\displaystyle  f\)가 증가함수도 감소함수도 아니라고 가정하면

아래의 두 경우가 존재한다. 두 경우 모두 연속함수의 성질인 사잇값의 정리로 모순을 유도할 수 있다.

(i) 어떤 세 점 \(\displaystyle  x_1 ,~x_2 ,~x_3 ~(x_1 <x_2 <x_3 )\)이 존재하여

\(\displaystyle  f (x_1 )<f(x_3 )<f(x_2 )\) 또는 \(\displaystyle  f (x_2 )<f(x_1 )<f(x_3 )\)

를 만족한다.

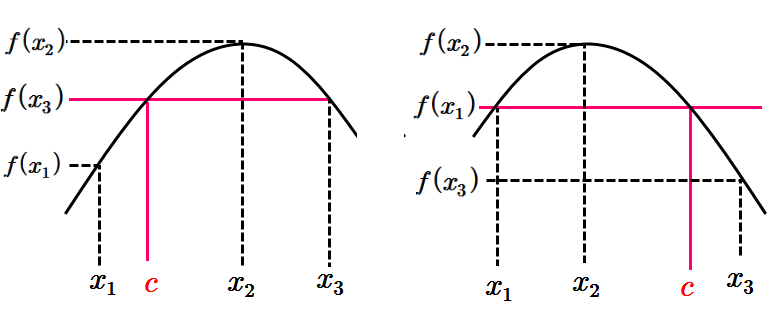
첫번째 그림에서 함수 \(\displaystyle f\)가 연속이고 \(\displaystyle f(x_1)<f(x_3 )<f(x_2 )\)이므로 사잇값의 정리에 의해

\(\displaystyle f(c)=f(x_3 )\)

를 만족하는 \(\displaystyle c\)가 구간 \(\displaystyle (x_1 ,~x_2 \)에 적어도 하나 존재한다.

그런에 이것은 함수 \(\displaystyle f\)가 \(\displaystyle 1-1\) 대응이라는 가정에 모순이다.

따라서 모든 \(\displaystyle  x_1 ,~x_2 ,~x_3 ~(x_1 <x_2 <x_3 )\)에 대하여 \(\displaystyle  f (x_1 )<f(x_2 )<f(x_3 )\)이어야 한다. 즉 증가함수이어야 한다.

또, 두 번째 그림에서는 위와 동일하게 하면 함수 \(\displaystyle f\)가 감소함수이어야 한다.

 

(ii) 어떤 세 점 \(\displaystyle  x_1 ,~x_2 ,~x_3 ~(x_1 <x_2 <x_3 )\)이 존재하여

\(\displaystyle  f (x_3 )<f(x_1 )<f(x_2 )\) 또는 \(\displaystyle  f (x_2 )<f(x_3 )<f(x_1 )\)

를 만족한다.

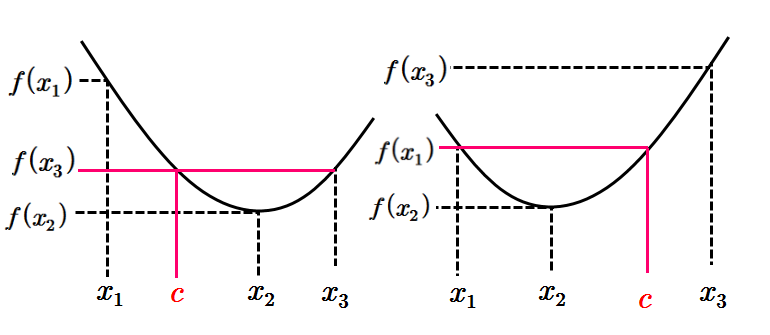
이 경우도 위의 (i)과 같이 하면 \(\displaystyle 1-1\)대응이라는 사실에 모순이 된다.

 

이제 \(\displaystyle f^{-1}\)가 연속함수임을 보이자.

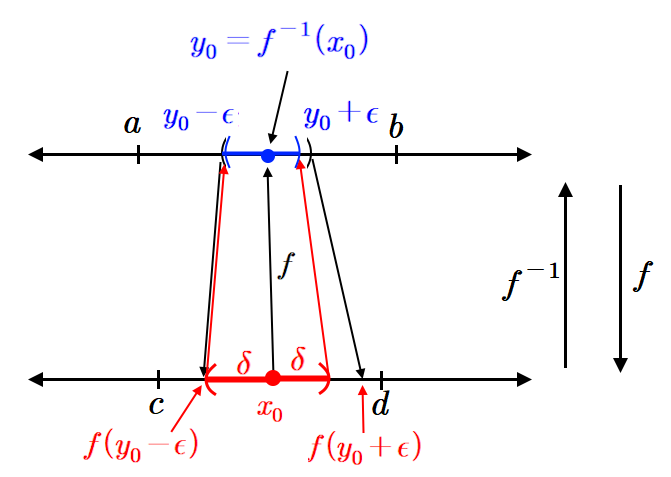
함수 \(\displaystyle f :(a,~b) \longrightarrow (c,~d)\)의 역함수 \(\displaystyle f^{-1}\)은

\(\displaystyle f^{-1}: (c,~d) \longrightarrow (a,~b)\)

이므로 \(\displaystyle f^{-1}\)의 정의역 \(\displaystyle (c,~d)\)의 임의의 원소 \(\displaystyle  x_0 \)에 대해 \(\displaystyle f^{-1}(x_0 ) =y_0 \in (a,~b)\)라 하자.

\(\displaystyle x=x_0 \)에서 함수 \(\displaystyle f^{-1}\)이 연속임을 보이자.

먼저 임의의 \(\displaystyle \epsilon>0\)에 대하여 구간 \(\displaystyle (y_0 -\epsilon,~y_0 +\epsilon) \subset (a,~b)\)을 생각해보자.

보조정리에 의해 일대일 대응인 연속함수 \(\displaystyle f\)는 증가함수(또는 감소함수)이므로 역함수 \(\displaystyle f^{-1}\)도 증가함수(또는 감소함수)이다. 따라서 \(\displaystyle y_0 -\epsilon < y_0 < y_0 +\epsilon \)에서

\(\displaystyle  f (y_0 -\epsilon) <  f(y_0)= x_0 <   f (y_0 +\epsilon)\)

여기서 \(\displaystyle \delta=\min \left\{ x_0 -  f(y_0-\epsilon),~f (y_0+\epsilon)-x_0 \right\}\)라 하면 다음 부등식이 성립한다.

\(\displaystyle  f (y_0 -\epsilon) \leq x_0 -\delta < x_0 < x_0 +\delta \leq f  (y_0 +\epsilon)\)

함수 \(\displaystyle f^{-1}\)가 증가함수이고 \(\displaystyle f^{-1}\circ f=I \) 임을 이용하면

\(\displaystyle  y_0 -\epsilon=f^{-1}(f(y_0 -\epsilon)) \leq f^{-1}(x_0 -\delta) <f^{-1} ( x_0)=y_0  < f^{-1}( x_0 +\delta ) \leq  f^{-1} (f(y_0 +\epsilon))=y_0 + \epsilon\)

즉, $\displaystyle ( f^{-1}( x_0 -\delta),~f^{-1}(x_0+\delta) )\subset  (y_0-\epsilon ,~y_+\epsilon) $

\(\displaystyle \left| x-x_0 \right|<\delta\)를 만족하는 모든 \(\displaystyle x\)는 \(\displaystyle \left| f^{-1} (x)-f^{-1}(x_0 ) \right| <\epsilon\)

을 만족하므로

역함수 \(\displaystyle f^{-1} \)는 \(\displaystyle x=x_0 \)에서 연속이다.