[킬러문항 21번] 2012년 가형 4월 교육청 21번 [더플러스수학]

https://tv.kakao.com/v/401140813

 

함수 $ f \left ( x \right ) =\ln \left ( 2x ^ {2} +1 \right ) $에 대하여 옳은 것만을 <보기>에서 있는 대로 고른 것은? [4점] [2012년 4월]

---

ㄱ. 모든 실수 $ x $에 대하여 $ f ' ( -x)=-f ' ( x) $이다.

ㄴ. $ f \left ( x \right ) $의 도함수 $ f ' \left ( x \right ) $의 최댓값은 $ \sqrt {2} $이다.

ㄷ. 임의의 두 실수 $ x _ {1} $, $ x _ {2} $에 대하여 $ \left | f \left ( x _ {1} \right ) -f \left ( x _ {2} \right ) \right | \leq \sqrt {2} \left | x _ {1} -x _ {2} \right | $이다.

---

① ㄱ                           ② ㄷ                            ③ ㄱ, ㄴ

④ ㄴ, ㄷ                       ⑤ ㄱ, ㄴ, ㄷ

 

 

정답 및 풀이를 보려면 아래를 클릭하세요.

 

 

정답 및 풀이

ㄱ. $ f ' \left ( x \right ) = \frac {4x} {2x ^ {2} +1} $이므로 $ f ' ( -x)=-f ' ( x) $ (참)

ㄴ. $$ f ' ' \left ( x \right ) = \frac {4 \left ( 2x ^ {2} +1 \right ) -4x \cdot 4x} {\left ( 2x ^ {2} +1 \right ) ^ {2} } = \frac {4 \left ( 1-2x ^ {2} \right )} {\left ( 2x ^ {2} +1 \right ) ^ {2} } $$

$ f ' ' \left ( x \right ) =0 $에서 $ x=- \frac {1} {\sqrt {2} } $ 또는 $ x= \frac {1} {\sqrt {2} } $

$$ \begin{array}{c|ccccc} x & \cdots & -\frac{1}{\sqrt{2}} & \cdots & \frac{1}{\sqrt{2}} & \cdots \\ \hline f’(x) & - & 0 & + & 0 & - \\ \hline f(x) & \nearrow & -\sqrt{2} & \searrow & \sqrt{2} & \nearrow\end{array}$$

$ \lim\limits _ {x \rightarrow - \infty } {f ' \left ( x \right )} = \lim\limits _ {x \rightarrow \infty } {f ' \left ( x \right )} =0 $이므로 $ y=f ' \left ( x \right ) $의  그래프는 그림과 같다.

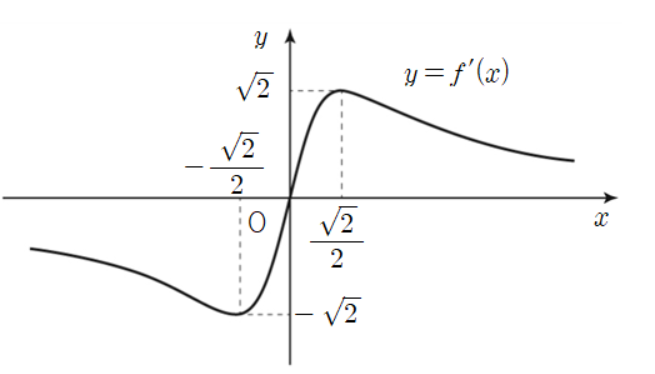
따라서 함수 $ f ' \left ( x \right ) $의 최댓값은 $ \sqrt {2} $이다. (참)

ㄷ. ⅰ) $ x _ {1} =x _ {2} $일 때, 주어진 부등식은 성립한다.

ⅱ)$ x _ {1} \neq x _ {2} $일 때, 닫힌 구간 $ \left [ x _ {1} ,~x _ {2} \right ] $에서 평균값의 정리에 의하여 $ \frac {f \left ( x _ {1} \right ) -f \left ( x _ {2} \right )} {x _ {1} -x _ {2} } =f ' \left ( c \right ) $인 $ c $가 열린 구간 $ \left ( x _ {1} ,~x _ {2} \right ) $에서 적어도 하나 존재한다.

ㄱ, ㄴ에 의하여 $ - \sqrt {2} \leq f ' \left ( x \right ) \leq \sqrt {2} $이므로

$$ \left | \frac {f \left ( x _ {1} \right ) -f \left ( x _ {2} \right )} {x _ {1} -x _ {2} } \right | = \left | f ' \left ( c \right ) \right | \leq \sqrt {2} $$이다.

$ \therefore $ ⅰ), ⅱ)에 의하여 임의의 두 실수 $ x _ {1} ,~x _ {2} $에 대하여 $ \left | f \left ( x _ {1} \right ) -f \left ( x _ {2} \right ) \right | \leq \sqrt {2} \left | x _ {1} -x _ {2} \right | $ (참)

따라서 옳은 것은 ㄱ, ㄴ, ㄷ