-
[평가원기출] 2011학년도 가형 9월 11번수능 모의고사 2019. 10. 5. 21:32
실수 전체의 집합에서 연속인 함수 $ f \left ( x \right ) $가 있다. $ 2 $ 이상인 자연수 $ n $에 대하여 폐구간 $ [0,1] $을 $ n $등분한 각 분점 (양 끝점도 포함)을 차례대로 $ 0=x _ {0} ,~x _ {1} ,~x _ {2} , ~\cdots ,~x _ {n-1} ,~x _ {n} =1 $이라 할 때, 옳은 것만을 <보기>에서 있는 대로 고른 것은? [4점][2010년 9월]
ㄱ. $ n=2m $ ($ m $은 자연수)이면 $ \sum\limits _ {k=0} ^ {m-1} \frac {f \left ( x _ {2k} \right )} {m} \leq \sum\limits _ {k=0} ^ {n-1} \frac {f \left ( x _ {k} \right )} {n} $이다.
ㄴ. $ \lim\limits _ {n \rightarrow \infty } {\sum\limits _ {k=1} ^ {n} \frac {1} {n} \left\{ \frac {f \left ( x _ {k-1} \right ) +f \left ( x _ {k} \right )} {2} \right\} = \int _ {0} ^ {1} {f \left ( x \right ) dx} } $
ㄷ. $ \sum\limits _ {k=0} ^ {n-1} \frac {f \left ( x _ {k} \right )} {n} \leq \int _ {0} ^ {1} {f \left ( x \right ) dx} \leq \sum\limits _ {k=1} ^ {n} \frac {f \left ( x _ {k} \right )} {n} $
① ㄱ ② ㄴ ③ ㄷ
④ ㄱ, ㄴ ⑤ ㄴ, ㄷ
https://tv.kakao.com/v/402658602

정답 및 풀이를 보려면 아래를 클릭하세요.
...더보기정답 ②
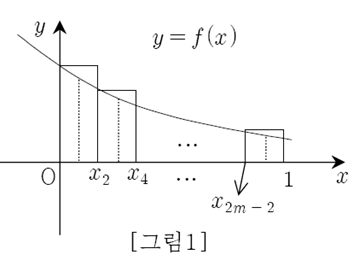
ㄱ. (반례)
$ x _ {2k+2} -x _ {2k} = \frac {2} {2m} = \frac {1} {m} $이므로
$ \sum\limits _ {k=0} ^ {m-1} \frac {f ( x _ {2k} )} {m} $은 [그림1]의 직사각형들의 넓이의 합을 나타낸다.
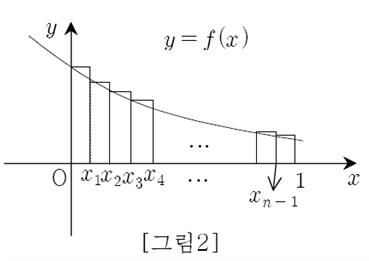
$ x _ {k+1} -x _ {k} = \frac {1} {n} $이므로
$ \sum\limits _ {k=0} ^ {n-1} \frac {f ( x _ {k} )} {n} $은 [그림2]의 직사각형들의 넓이의 합을 나타낸다.
따라서, $ \sum\limits _ {k=0} ^ {m-1} \frac {f ( x _ {2k} )} {m} > \sum\limits _ {k=0} ^ {n-1} \frac {f ( x _ {k} )} {n} $이다. (거짓)
ㄴ. $ x _ {k} = \frac {k} {n} $이므로
$ \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} \frac {1} {n} \left\{ \frac {f ( x _ {k-1} )+f ( x _ {k} )} {2} \right\} $
$ = \frac {1} {2} \left\{ \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} f ( x _ {k-1} ) \frac {1} {n} + \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} f ( x _ {k} ) \frac {1} {n} \right\} $
$ = \frac {1} {2} \left\{ \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} f \left ( \frac {k-1} {n} \right ) \frac {1} {n} + \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} f \left ( \frac {k} {n} \right ) \frac {1} {n} \right\} $
$ = \frac {1} {2} \left\{ \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=0} ^ {n-1} f \left ( \frac {k} {n} \right ) \frac {1} {n} + \lim\limits _ {n \rightarrow \infty } {} \sum\limits _ {k=1} ^ {n} f \left ( \frac {k} {n} \right ) \frac {1} {n} \right\} $
$ = \frac {1} {2} \left\{ \int _ {0} ^ {1} {} f ( x)dx+ \int _ {0} ^ {1} {} f ( x)dx \right\} $
$ = \int _ {0} ^ {1} {} f ( x)dx $ (참)
ㄷ. (반례) ㄱ의 [그림2]에서
$ \int _ {0} ^ {1} {} f ( x)dx $는 곡선 $ y=f ( x) $와 $ x $축 및 두 직선 $ x=0,x=1 $로 둘러싸인 부분의 넓이이고, $ \sum\limits _ {k=0} ^ {n-1} \frac {f ( x _ {k} )} {n} $은 직사각형들의 넓이의 합을 나타내므로
$ \sum\limits _ {k=0} ^ {n-1} \frac {f ( x _ {k} )} {n} > \int _ {0} ^ {1} {} f ( x)dx $ (거짓)
따라서, 보기 중 옳은 것은 ㄴ이다.
'수능 모의고사' 카테고리의 다른 글
[평가원 기출] 2015학년도 나형 6월 30번 (0) 2019.10.12 [평가원기출] 2007학년도 가형 9월 12번 (0) 2019.10.05 [킬러문항] 2017학년도 가형 6월 평가원 21번 [더플러스수학] (0) 2019.09.23 [킬러문항 21번] 2012년 가형 4월 교육청 21번 [더플러스수학] (0) 2019.09.23 [2019학년도 나형 6월30번] 평가원 나형 6월30번 (0) 2019.09.11