[삼사관학교 기출] 2016학년도 A 삼사 21번

https://tv.kakao.com/v/402947937

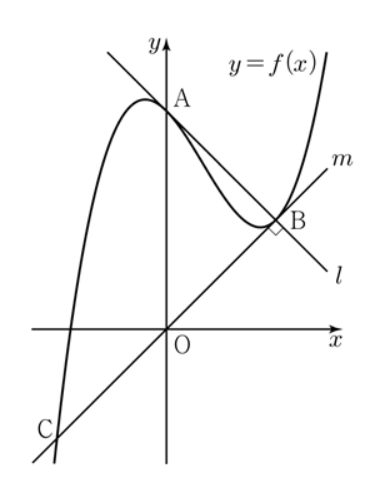
최고차항의 계수가 $ 1 $인 삼차함수 $ f ( x) $에 대하여 곡선 $ y=f ( x) $가 $ y $축과 만나는 점을 $ \rm A $라 하자. 곡선 $ y=f ( x) $ 위의 점 $ \rm A $에서의 접선을 $ l $이라 할 때, 직선 $ l $이 곡선 $ y=f ( x) $와 만나는 점 중에서 $ \rm A $가 아닌 점을 $ \rm B $라 하자. 또, 곡선 $ y=f ( x) $ 위의 점 $ \rm B $에서의 접선을 $ m $이라 할 때, 직선 $ m $이 곡선 $ y=f ( x) $와 만나는 점 중에서 $ \rm B $가 아닌 점을 $ \rm C $라 하자. 두 직선 $ l $, $ m $이 서로 수직이고 직선 $ m $의 방정식이 $ y=x $일 때, 곡선 $ y=f ( x) $ 위의 점 $ \rm C $에서의 접선의 기울기는? (단, $ f ( 0)>0 $이다.) [4점][2016년 사관학교]

① $ 8 $                           ② $ 9 $                          ③ $ 10 $

④ $ 11 $                          ⑤ $ 12 $

 

 

 

정답 및 풀이를 보려면 아래를 클릭하세요.

 

정답 ②

(풀이)

점 $ \rm B $, $ \rm C $의 $ x $좌표를 각각 $ b $, $ c $라 하면

직선 $ m $과 곡선 $ y=f ( x) $가 두 점 $ \rm B $, $ \rm C $에서 만나고 $ f ( x) $가 최고차항의 계수가 $ 1 $인 삼차함수이므로

$$ f ( x)-x= ( x-b) ^ {2} ( x-c) ~\cdots\cdots~(\mathrm{i})$$

로 놓을 수 있다.

점 $ \rm B $는 직선 $ y=x $ 위의 점이므로 좌표는 $ ( b,~b) $이다. 직선 $ l $은 점 $ \rm B $를 지나며 직선 $ y=x $와 수직이므로 기울기가 $ -1 $이다. 따라서 직선 $ l $의 방정식은 $ y=-x+2b $이다.

점 $ \rm A $는 직선 $ l $의 $ y $절편이므로 점 $ \rm A $의 좌표는 $ ( 0,~2b) $, 즉 $ f ( 0)=2b $이다.

문제의 조건에서 $ f ( 0)>0 $이므로 $ b>0 $이다.

($\mathrm{i}$)의 양변에 $ x=0 $을 대입하면

$$ f ( 0)  =-b ^ {2} c=2b $$

$$ \therefore~bc=-2 ~ (\because~ b>0 )~\cdots\cdots(\mathrm{ii})$$

직선 $ l $은 점 $ \rm A $에서 곡선 $ y=f ( x) $와 접하므로 $ f ' ( 0)=-1 $이다.

($\mathrm{i}$)의 양변을 $ x $에 대하여 미분하면

$$ f ' ( x)-1=2 ( x-b) ( x-c)+ ( x-b) ^ {2} ~\cdots\cdots (\mathrm{iii})$$

($\mathrm{iii}$) 의 양변에 $ x=0 $을 대입하면

$$ f ' ( 0)-1   =2bc+b ^ {2}   =-2 $$

$$ b ^ {2} =2 ~ (\because~ (\mathrm{ii}))$$

$$ \therefore~b= \sqrt {2} ~ ~(\because~ b>0 )$$

$ b= \sqrt {2} $를 ($\mathrm{ii}$)에 대입하면 $ c=- \sqrt {2} $

구하는 값은 $ f ' ( c) $이므로 ($\mathrm{iii}$)에 $ x=c $를 대입하면

$$ f ' ( c)-1= ( c-b) ^ {2} = ( -2 \sqrt {2} ) ^ {2} =8 $$

$$\because~ f ' ( c)=9 $$

 

<다른 풀이>

$\mathrm {A}$의 $x$좌표는 $0$이고 $\mathrm {B}$의 좌표를 $(\alpha,~f(\alpha))$로 놓자. 또, $\mathrm {C}$의 좌표를 $(\beta,~f(\beta))$로 놓자. 그러면 직선 $y=l(x)$과 $y=f(x)$에서 $y$를 소거한 $3$차 방정식

$$f(x)=l(x),~~f(x)-l(x)=0~\cdots\cdots ~(\mathrm {i})$$

의 근은 $0,~\alpha,~\alpha$이다.

또, 직선 $y=x$과 $y=f(x)$에서 $y$를 소거한 $3$차 방정식

$$f(x)=x,~~f(x)-x=0~\cdots\cdots~(\mathrm{ii})$$

의 근은 $\beta,~\alpha,~\alpha$이다. 두 삼차방정식 (i), (ii)의 3차항의 계수와 2차항의 계수는 서로 같으므로 세 근의 합은 서로 같다. 즉

$$0+0+\alpha=\beta+\alpha+\alpha$$

$$\therefore~\beta=-\alpha$$

따라서 (ii)는 다음과 같이 놓을 수 있다.

$$f(x)-x=(x+\alpha)(x-\alpha)^2,~~f(x)=(x+\alpha)(x-\alpha)^2 +x~\cdots\cdots~(\mathrm{iii})$$

한편 점 $\mathrm A$에서의 접선은 직선 $y=x$와 서로 수직이므로 $f '(0)=-1$이다.

(iii)에서 $$f'(x)=  (x-\alpha)^2 +2(x+\alpha)(x-\alpha) +1 ~\cdots\cdots ~(\mathrm{iv})$$

$$f'(0)=\alpha^2 -2\alpha^2 +1=-1,~\therefore ~\alpha^2 =2$$

$\alpha >0$이므로 $\alpha=\sqrt2$이다.

따라서 (iv)에서 $f'(x )$는

$$f'(x)=  (x-\sqrt2 )^2 +2(x+\sqrt2 )(x-\sqrt2 ) +1   $$

$f'(-\sqrt2 )$는 $$\begin{align}f'(2)&=  (-\sqrt2 -\sqrt2 )^2 +2(-\sqrt2 +\sqrt2 )(-\sqrt2-\sqrt2 ) +1 \\&=9 \end{align} $$

$$\therefore~f'(-\sqrt2 )=9 $$

 

과학고 내신대비와 대학입시를 위해서는 다음의 글을 참조하세요. 다양한 글이 있습니다.

http://mathhowtosolveit.com/%EA%B3%BC%ED%95%99%EA%B3%A0-%ED%95%99%EB%85%84%EB%B3%84-%EB%82%B4%EC%8B%A0%EB%8C%80%EB%B9%84-%EC%98%88%EC%83%81%EB%AC%B8%EC%A0%9C

더플러스수학https://www.youtube.com/@THEPLUSMATH/channels

더플러스수학 블로그https://plusthemath.tistory.com/

더플러스수학 네이버블로그 https://m.blog.naver.com/plusthemath