조합론적 증명

조합론적 증명(combinatorial proof)
https://en.wikipedia.org/wiki/Combinatorial_proof
A proof by double counting. A combinatorial identity is proven by counting the number of elements of some carefully chosen set in two different ways to obtain the different expressions in the identity. Since those expressions count the same objects, they must be equal to each other and thus the identity is established.
 
조합론에서 조합수학의 항등식을 다음과 같이 증명하는 것이다.
한가지 대상을 서로 다른 두가지 방식으로 개수를 셈으로써 좌-우의 식(Left-Hand-Side=Right-Hand-Side)이 같음을 보이는 것이다.
조합론적으로 항등식을 증명하기 위해는 세고자 하는 대상을 서로 다른 방법으로 표현하는 것이 필요하다. 즉 “좌변의 식이 대상을 세는 방법” = “우변의 식이 대상을 세는 방법”
 

1. $$\textcolor{red}{{}_n \mathrm C _r = {}_n \mathrm C_{n-r}}$$

 
좌변 : $n$명의 대입지원자 중 $k$명을 합격시키는 방법의 수
우변 : $n$명의 대입지원자 중 $n-k$명을 불합격시키는 방법의 수
 
또는
좌변 : $n$명 중 사탕을 줄 $k$명을 선택하는 방법의 수
우변 : $n$명의 중 사탕을 주지 않을 $n-k$명을 선택하는 방법의 수
 
2. 파스칼의 항등식
$n \geq r \geq 1$인 정수 $n,~r$에 대하여
$$\textcolor{red}{{}_n \mathrm C _r = {}_{n-1} \mathrm C_{r-1}+{}_{n-1} \mathrm C_{r}}$$
 
좌변 : 월드컴 축구 경기를 응원하기 위하여 철수를 포함한 $n$명 중에서 face-painting할 $k$명 선택하는 방법의 수
$${}_{n} \mathrm C_{r}$$
우변 :
($\mathrm{i}$) 철수와 $k-1$명을 선택하여 모두 $k$명을 face-painting하는 경우의 수
($\mathrm{ii}$) 철수를 제외한 $k$명을 선택하여 모두 $k$명을 face-painting하는 경우의 수
($\mathrm{i}$)과 ($\mathrm{ii}$)는 공통부분이 없으므로 합의 법칙에 의해
$${}_{n-1} \mathrm C_{r-1}+{}_{n-1} \mathrm C_{r}$$
$$\therefore ~{}_{n} \mathrm C_{r} = {}_{n-1} \mathrm C_{r-1}+{}_{n-1} \mathrm C_{r}$$
 
3. 반더몬드 항등식 (Vandermonde's Identity)
$$\textcolor{red}{{}_{m+n} \mathrm C _{r} =  \sum_{k=0}^{r} {}_m \mathrm C_k ~ {}_n \mathrm C _{r-k} }$$
 
$m$명의 남자와 $n$명의 여자로 이루어진 집합에서
좌변 : 총 $m+n$명 중 $r$명을 뽑는 방법의 수
우변 :

남자	$0$	$1$	$2$	$\cdots$	$k$	$\cdots$	$r$
여자	$r$	$r-1$	$r-2$	$\cdots$	$r-k$	$\cdots$	$0$
개수	${}_{m} \mathrm C_{ 0} \times {}_{n}\mathrm C _{r}$	${}_{m} \mathrm C_{ 1} \times {}_{n}\mathrm C _{r-1}$	${}_{m} \mathrm C_{ 2} \times {}_{n}\mathrm C _{r-2}$	$\cdots$	${}_{m} \mathrm C_{ k} \times {}_{n}\mathrm C _{r-k}$	$\cdots$	${}_{m} \mathrm C_{ r} \times {}_{n}\mathrm C _{0}$

 
서울대 본고사 문제
https://plusthemath.tistory.com/135

[서울대 본고사] 1994학년도 서울대 본고사 문제

 
따름 정리
$${}_{2n} \mathrm C _{n} =  \sum_{k=0}^{n} \left \{ {}_n \mathrm C_k \right\}^2$$
 
예 비슷한 상황을 만들어서 다음을 보여보자.
$${}_{2n} \mathrm C _{2} = 2 {}_n \mathrm C_2 +n^2$$
 
예
$${}_{n+1} \mathrm C _{r+1} = \sum_{k=r}^{n} {}_k \mathrm C_r$$
 
집합 $S=\left\{1,~2,~3,~\cdots,~n,~n+1 \right\}$를 생각하자. 이 집합의 부분집합의 개수를 두가지 방법으로 세어보자.
좌변 : 집합 $S$의 부분집합 중 원소의 개수가 $r+1$개인 부분집합의 개수는 $n+1$개의 원소 중 $r+1$개를 뽑는 조합의 수와 같다.
$${}_{n+1}\mathrm C _{r+1}$$
우변 : 집합 $S$의 부분집합 중 원소의 개수가 $r+1$개인 부분집합을 최대수를 기준으로 분류하면 최대수가 $r+1,~r+2,~r+3,~\cdots,~n+1$인 경우가 있다.
최대수가 $r+1$인 경우는 $1,~2,~\cdots,~r$중 $r$개를 뽑는 방법의 수 : ${}_r \mathrm C _r$
최대수가 $r+2$인 경우는 $1,~2,~\cdots,~r+1$중 $r$개를 뽑는 방법의 수 : ${}_{r+1} \mathrm C _r$

$\vdots$

최대수가 $k+1$인 경우는 $1,~2,~\cdots,~k$중 $r$개를 뽑는 방법의 수 : ${}_k \mathrm C _r$
최대수가 $n+1$인 경우는 $1,~2,~\cdots,~n$중 $r$개를 뽑는 방법의 수 : ${}_n \mathrm C _r$
즉
$${}_r \mathrm C _r + {}_r \mathrm C _r +{}_{r+1} \mathrm C _r + \cdots +{}_{n-1} \mathrm C _r + {}_n \mathrm C _r = \sum_{k=r}^n {}_k \mathrm C_r$$
 
$$\therefore~{}_r \mathrm C _r + {}_r \mathrm C _r +{}_{r+1} \mathrm C _r + \cdots +{}_{n-1} \mathrm C _r + {}_n \mathrm C _r = \sum_{k=r}^n {}_k \mathrm C_r ={}_{n+1}\mathrm C _{r+1}$$
 
참고 물론 최소수를 기준으로 분류해도 된다. 그러면
$${}_n \mathrm C _r + {}_{n-1} \mathrm C _r +{}_{n-2} \mathrm C _r + \cdots +{}_{r+1} \mathrm C _r + {}_{r} \mathrm C _r = \sum_{k=1}^{n-r} {}_{n-k} \mathrm C_r$$
위의 과정을 $(0,~0)$에서 $(n-r,~r+1)$로 최단거리로 가는 방법의 수로도 설명이 가능하다.
아래 그림은 $(6,~6)$으로 가는 길잡이의 수를 가지고 위의 과정을 설명하겠다.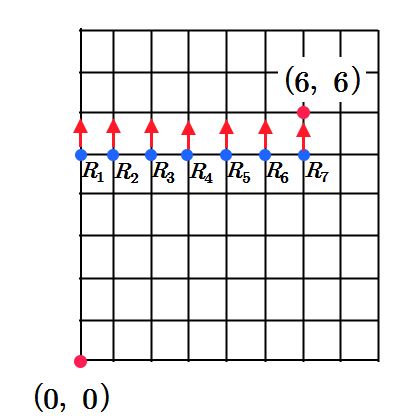

먼저 $(0,~0)$에서 $(6,~6)$으로 가는 최단거리의 가는 방법의 수는 $\frac{(6+6)!}{6! \times 6!}= {}_{12} \mathrm C _{6}$이다.
이 방법의 수를 다르게 세어보자.
$(0,~0)$에서 $R_1$으로 간 후 화살표 방향으로 가서 $(6,~6)$에 도달하는 방법의 수 : ${}_5 \mathrm C _5$
$(0,~0)$에서 $R_2$으로 간 후 화살표 방향으로 가서 $(6,~6)$에 도달하는 방법의 수 : ${}_6 \mathrm C _5$
$(0,~0)$에서 $R_3$으로 간 후 화살표 방향으로 가서 $(6,~6)$에 도달하는 방법의 수 : ${}_7 \mathrm C _5$

$\vdots$

$(0,~0)$에서 $R_1$으로 간 후 화살표 방향으로 가서 $(6,~6)$에 도달하는 방법의 수 : ${}_{11} \mathrm C _5$
따라서 두가지로 경우의 수를 세면 서로 같으므로
$${}_{12} \mathrm C _{6}={}_{5} \mathrm C _{5}+{}_{6} \mathrm C _{5}+{}_{7} \mathrm C _{5}+\cdots+{}_{11} \mathrm C _{5}=\sum_{k=5}^{11} {}_{k} \mathrm C _{5}$$
이처럼 $(0,~0)$에서 $(n-r,~r+1)$로 최단거리로 가는 방법의 수를 두가지로 구하면
$${}_r \mathrm C _r + {}_r \mathrm C _r +{}_{r+1} \mathrm C _r + \cdots +{}_{n-1} \mathrm C _r + {}_n \mathrm C _r = \sum_{k=r}^n {}_k \mathrm C_r ={}_{n+1}\mathrm C _{r+1}$$
이다.
 
In-and-Out Formula
$$\textcolor{red}{r {}_{n}\mathrm C _{r}= n {}_{n-1} \mathrm C_{r-1}}$$
좌변 : $n$명의 사람 중에서 국회의원 $r$명을 뽑고 그 안의 $r$명 중 한 명의 의장을 뽑는 방법의 수
$${}_{n} \mathrm C _r \times {}_r \mathrm C _{1} = r {}_n \mathrm C _r$$
우변 : $n$명 중 미리 밖에서 국회의장 한 명을 뽑고, $n-1$명 중 $r-1$명의 국회의원을 뽑는 방법의 수
$${}_{n} \mathrm C _{1} \times {}_{n-1} \mathrm C _{r-1} = n \times {}_{n-1} \mathrm C _{r-1}$$
$$\therefore~r {}_n \mathrm C _r = n \times {}_{n-1} \mathrm C _{r-1}$$
 
또 다른 관점에서 증명하자. 조금 있다가 완성하자. ㅠㅠ
집합 $S= \left\{1,~2,~3,~\cdots,~n \right\}$의 원소 $i$와 원소의 개수가 $k$개인 부분집합을 생각하자.
좌변 :  $i$를 포함
 
https://plusthemath.tistory.com/406

[한양대수리논술] 2020학년도 한양대 자연계열 논술(오후1)[더플러스수학]

 
더플러스수학학원
울산 남구 대공원입구로21번길 45-1 2층
https://naver.me/G4I5PTH1

더플러스수학학원 : 네이버

더플러스수학학원 신정지점
울산 남구 문수로423번길 8 309호
https://naver.me/FTOL1Hgt

더플러스수학학원 신정지점 : 네이버