[평가원 기출-킬러문항] 2018학년도 나형 9월 30번

두 함수 $ f ( x) $와 $ g ( x) $가

$$ \begin{align} &f ( x)= { \begin {cases} ~0 &( x \leq 0)\\~x &( x>0)\end {cases} } \\& g ( x)= { \begin {cases} ~x ( 2-x) &( \left | x-1 \right | \leq 1)\\~0 &( \left | x-1 \right | >1)\end {cases} } \end{align}$$

이다. 양의 실수 $ k,~a,~b $ $ ( a<b<2) $에 대하여, 함수 $ h ( x) $를

$$ h ( x)=k \left\{ f ( x)-f ( x-a)-f ( x-b)+f ( x-2) \right\} $$

라 정의하자. 모든 실수 $ x $에 대하여 $ 0 \leq h ( x) \leq g ( x) $일 때, $ \int _ {0} ^ {2} { \left\{ g ( x)-h ( x) \right\} dx} $의 값이 최소가 되게 하는 $ k,~a,~b $에 대하여 $ 60 ( k+a+b) $의 값을 구하시오. [4점]

 

 

 

정답 및 풀이을 보려면 아래를 클릭하세요.

 

정답 200

주어진 함수 $ h ( x) $를 $ x=a $와 $ x=b $를 기준으로 구간을 나누어 정의해 보면

$$ h ( x)= { \begin {cases} ~~~~~~0~~~~ &( x \leq 0)\\~~~~~kx~~~~ &( 0<x \leq a)\\~~~~~ka~~~~ &( a<x \leq b)\\k ( a+b-x)~ &( b<x \leq 2)\\k ( a+b-2)~ &( x>2)\end {cases} } $$

구하는 값은 $ \int _ {0} ^ {2} {} \left\{ g ( x)-h ( x) \right\} dx $의 최소이고

$ \int _ {0} ^ {2} {} g ( x)dx $의 값은 일정하므로 $ \int _ {0} ^ {2} {} h ( x)dx $가 최대일 때를 구하자.

모든 실수 $ x $에 대하여 $ 0 \leq h ( x) \leq g ( x) $이므로

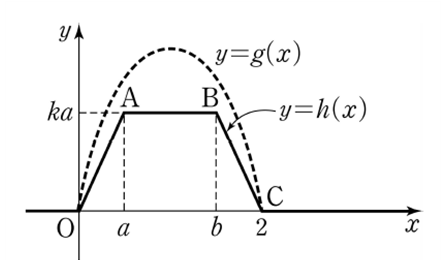
$ h ( x) $는 사다리꼴이고 $ g ( x) $에 접하는 사다리꼴일 때 $ \int _ {0} ^ {2} {} h ( x)dx $의 값이 최대가 된다. 따라서

$ h ( a)=g ( a) $, $ h ( 2)=g ( 2) $이므로

$ ka=a ( 2-a) $, $ k ( a+b-2)=0 $

$ \therefore ~k=2-a $, $ a+b=2 $ $ ( \because k \neq 0) $

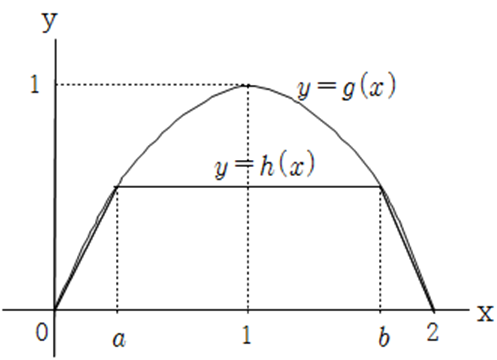
$ a $, $ b $는 $ x=1 $에 대하여 대칭이고

$ a=1-t $, $ b=1+t $라 하면 사다리꼴 넓이 공식에 의해

$$\begin{align} \int _ {0} ^ {2} {} h ( x)dx &= \frac {1} {2} \times \left ( 2t+2 \right ) \left ( 1+t \right ) \left ( 1-t \right ) \\& = \left ( 1+t \right ) ^ {2} \left ( 1-t \right ) $ $ ( 0<t \leq 1) \end{align}$$

$ p ( t)= \left ( 1+t \right ) ^ {2} \left ( 1-t \right ) $ $ ( 0<t \leq 1) $ 라 하면

$$ \begin{align} p ' ( t) &=2 \left ( 1+t \right ) \left ( 1-t \right ) - \left ( 1+t \right ) ^ {2} \\& = ( 1+t) ( 1-3t) \end{align}$$

$ t= \frac {1} {3} $일 때 최대가 된다.

따라서 $ a= \frac {2} {3} $, $ b= \frac {4} {3} $, $ k= \frac {4} {3} $

$ \therefore ~60 ( a+b+k)=200 $

 

https://tv.kakao.com/v/403675715