[더플러스수학]2020학년도 수능 가형 21번[킬러문항]

실수 $t$에 대하여 $y=e^x$ 위의 점 $(t,~e^t )$에서의 접선의 방정식을 $y=f(x)$라 할 때, 함수 $y=|f(x)+k-\ln x |$가 양의 실수 전체에서 미분가능하도록 하는 실수 $k$의 최솟값을 $g(t)$라 하자.
두 실수 $a,~b$에 대하여 $\int_{a}^{b} g(t)dt=m$이라 할 때, <보기>에서 옳은 것만을 있는 대로 고른 것은? [$4$점]

| 보기 |

---

ㄱ. $m<0$이 되도록 하는 두 실수 $a,~b~(a<b)$가 존재한다.
ㄴ. 실수 $c$에 대하여 $g(c)=0$이면 $g(-c)=0$이다.
ㄷ. $a=\alpha,~b=\beta~(\alpha<\beta)$일 때 $m$의 값이 최소이면 $\frac{1+g'(\beta)}{1+g'(\alpha)}<-e^2$이다.

---

① ㄱ               ② ㄴ                ③ ㄱ, ㄴ
④ ㄱ, ㄷ           ⑤ ㄱ, ㄴ, ㄷ

https://tv.kakao.com/v/403829784

 

 

정답 및 풀이을 보려면 아래를 클릭하세요.

 

정답  5번

먼저 $x=t$에서의 접선을 구하면

$$f ( x)=e ^ {t} ( x-t)+e ^ {t}$$

$y= \left | f ( x)+k-\ln x \right |$가 양의 실수 전체의 집합에서 미분가능하면서 $k$값이 최소가 되는 경우는, 접선 $y=f ( x)$를 $y$축으로 $k$만큼 평행이동한 직선이 $y=\ln x$에 접할 때이다. 즉

$$y=e ^ {t} ( x-t)+e ^ {t} +k ~ \cdots \cdots ~(\mathrm{i})$$  가 $y=\ln x$에 접하는 접선이므로

$$( \ln x) ' =e ^ {t} ,~ \frac {1} {x} =e ^ {t}$$

$\therefore$ $x=e ^ {-t}$

따라서 접점의 좌표는 $( e ^ {-t} ,~-t)$

이것을 ($\mathrm{i}$)에 대입하면

$$-t=e ^ {t} ( e ^ {-t} -t)+e ^ {t} +k$$

$\therefore$ $k= ( t-1)e ^ {t} - ( 1+t)$

$\therefore$ $g ( t)= \left ( t-1 \right ) e ^ {t} - \left ( 1+t \right )$

이제 $y=g ( t)$의 그래프를 그리자.

$$g ' ( t)=e ^ {t} + ( t-1)e ^ {t} -1=te ^ {t} -1$$

$$g '' ( t)=e ^ {t} +te ^ {t} = ( 1+t)e ^ {t} =0$$

$t=-1$에서 $g ' ( t)$는 극솟값을 갖는다. 또, $g ' ( -1)=-e ^ {-1} -1<0$

따라서 $y=g ' ( t)$의 개형은 다음과 같다.

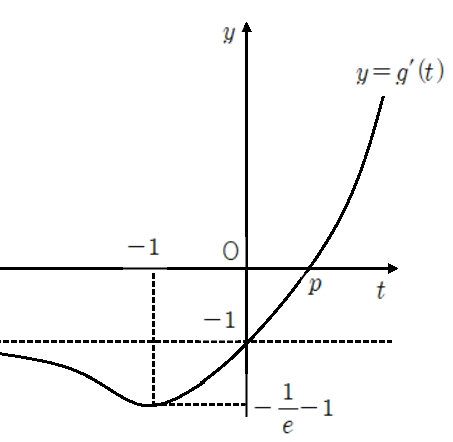
한편 $\lim\limits _ {t \rightarrow \infty } {g ( t)= \lim\limits _ {t \rightarrow \infty } { ( te ^ {t} -1)= \infty } }$ 이고

$$\begin{align} \lim\limits _ {t \rightarrow - \infty } {g ( t)} &= \lim\limits _ {t \rightarrow - \infty } { ( te ^ {t} -1)} \\&= \lim\limits _ {x \rightarrow \infty } { ( -xe ^ {-x} -1)=-1} \end{align}$$

따라서 $te ^ {t} -1=0$인 양의 실근이 하나 존재하므로, 이를 $p$라 하자. 그러면 $y=g ( t)$는 $t=p$에서 극솟값이자 최솟값을 갖는다.

$$g ( p)= ( p-1)e ^ {p} - ( 1+p)=pe ^ {p} -e ^ {p} -1-p=-e ^ {p} -1<0$$

또한 $$\lim\limits _ {t \rightarrow \infty }  g ( t)=  \lim\limits _ {t \rightarrow \infty } {e ^ {t} ( t-1)- ( t+1)= \infty }$$

$$\begin{align} \lim\limits _ {t \rightarrow - \infty } g ( t) &= \lim\limits _ {t \rightarrow - \infty }  e ^ {t} ( t-1)- ( t+1) \\&= \lim\limits _ {x \rightarrow \infty }   \frac {-x-1} {e ^ {x} } - ( -x+1) \\&= \infty   \end{align}$$

따라서 증감표는 다음과 같다.

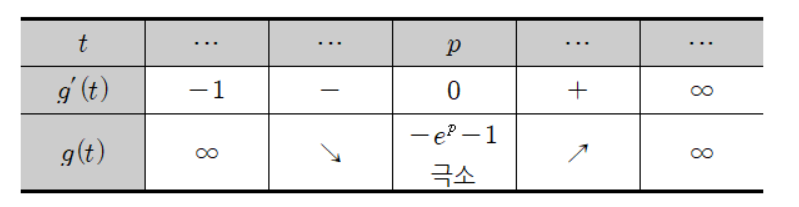
한편 $g ( 0)=-2<0$이므로 방정식 $g ( t)=0$는 양의 실근 하나와 음의 실근 하나를 가진다. 이를 각각 $q,~r$ ($q<0<r$)이라 두자. 또, $g ( 1)=-2<0$이므로 $r>1$이다.

이를 종합하여 $y=g ( t)$의 개형을 그리면 다음과 같다.

ㄱ. $y=g ( t)$는 서로 다른 두 실근을 가지고, $g ( t)<0$인 구간이 존재하므로 $\int _ {a} ^ {b} {g ( t)dt<0}$을 만족하는 순서쌍 $( a,~b)$가 존재한다.$( q \leq a<b \leq r)$ (참)

ㄴ. $g ( c)=0$이라 하면 $$e ^ {c} ( c-1)- ( c+1)=0$$

$$\begin{align} g ( -c) &=e ^ {-c} ( -c-1)- ( -c+1) \\& =e ^ {-c} \left\{ - ( c+1)+ ( c-1)e ^ {c} \right\} \\&=e^{-c} g ( c)=0 \end{align}$$

$\therefore ~g ( -c)=0$ (참)

ㄷ. 그림에서 $\alpha =p$, $\beta =q$일 때 $m= \int _ {\alpha } ^ {\beta } {g ( t)dt}$가 최소가 된다. 또, $g ( \alpha )=0$이므로 ㄴ에 의해 $g ( - \alpha )=0$이다. $g ( t)=0$의 근이 두 개밖에 없으므로 $\beta =- \alpha$이다.

$g ' ( t)=te ^ {t} -1$에서 $g ' ( \alpha )+1= \alpha e ^ {\alpha } ,~ g ' ( \beta )+1= \beta e ^ {\beta }$이므로

$$\begin{align} \frac {1+g ' ( \beta )} {1+g ' ( \alpha )} = \frac {\beta e ^ {\beta } } {\alpha e ^ {\alpha } } = \frac {\beta e ^ {\beta } } {- \beta e ^ {- \beta } } =-2e ^ {2 \beta } ~ \cdots \cdots ~(\mathrm{ii})\end{align}$$

$g ( 1)=-2<0$이므로 $\beta >1$이다. 따라서 $e ^ {2 \beta } >e ^ {2}$

$(\mathrm{ii})$에서 $-2e ^ {2 \beta } <-2e ^ {2}$ (참)