[수학의 기초] 함수에 대하여(3) - 일대일대응 역함수

 

Definition1.(일대일 대응) Let $X,~Y$ be sets, and let $f~ :~ X \longrightarrow Y$ be a function. We say that $f$ is bijective if $f$ is both injective and surjective.

bijective는 일대일 대응이으로 치역과 공역이 같은 함수이면서 동시에 $1-1$ 함수이다. 

 

Proposition 2. Let $X,~Y$ be sets, and let $f~ :~ X \longrightarrow Y$ be a function. Then $f$ is bijective if and only if $\forall y \in Y$, $\exists! x \in X$ such that \(f(x) = y\), 즉 임의의 \(y \in Y\)에 대하여 \(y=f(x) \)를 만족하는 \(x \in X\)가 오직 하나 존재한다.

(참고) 여기서 $\exists!$는 오직 하나 존재한다는 뜻이다.

(증명) ($\Rightarrow$) $f$가 1-1대응(bijective)라고 가정하자. 그러면 $f$가 치역과 공역이 같은 함수(surjective)이므로 정의에 의해

임의의 $y \in Y$에 대하여 적당한 $x \in X$가 존재하여 $y=f(x)$이다.

이제 $y=f(x)$를 만족하는 $x$가 두개 존재한다고 가정하자. 즉 $y=f(x_1 )=f(x_2 )$, $x_1 \neq x_2~\cdots\cdots \mathrm {(a)}$

함수 $f$가 $1-1$함수이므로 정의에 의해

$$f(x_1 )=f(x_2 ) ~\Longrightarrow~ x_1 =x_2$$

이것은 (a)에 모순이다. 따라서 $y=f(x)$를 만족하는 $x$가 오직 하나 존재한다.

($\Leftarrow$) 임의의 $y \in Y$에 대하여 $y=f(x)$를 만족하는 $x$가 집합 $X$에 오직 하나 존재한다고 가정하자.

일단 임의의 $y \in Y$에 대하여 $y=f(x)$를 만족하는 $x$가 집합 $X$에 존재하므로 함수 $f$는 정의에 의해 치역과 공역이 같은 함수이다.

이 함수가 $1-1$함수임을 보이자.

귀류법으로 증명하자.

$x_1 \neq x_2 $인 $x_1 ,~x_2 \in X$에 대하여 $f(x_1 )=f(x_2 )=y \in Y$를 만족하는 $x_1,~x_2$가 존재한다고 하자. 가정에 의해 $x_1 =x_2$이다. 이는 $x_1 \neq x_2 $와 모순이다. 따라서 함수 $f$는 $1-1$함수이다.

따라서 명제는 증명끝났다.                                                                               $\Box$

 

Theorem 3. Let $X,~Y,~Z$ be sets, and let $f~ :~ X \longrightarrow Y$ and $g~ :~ Y \longrightarrow Z$ be functions. If f and g are bijective, then $g \circ f$ is bijective.

(증명) [수학의 기초] 함수에 대하여(2)의 정리2와 5에 의해 당연히 증명된다.

 

[수학의 기초] 함수에 대하여(2) - 함수의 종류

 

위의 정리의 역은 성립하지 않는다. 

그림1

위의 두 함수 $f,~g$는 모두 일대일 대응(bijection)이 아니다. 그렇지만 $g \circ f$는 $1-1$대응이다.

 

Denition 4. Let $X,~ Y$ be sets, and let $f~ :~ X \longrightarrow Y$ be a function. A function $g~ :~ Y \longrightarrow X$ is called a left inverse to $f$ if $g \circ f=I_X$. A function $h~ :~ Y \longrightarrow X$ is called a right inverse to f if $f \circ h=I_Y$. A function from $Y$ to $X$ is called a two-sided inverse, or sometimes just inverse, to f if it is both a left and right inverse.

예를 들면 다음 그림을 보자.

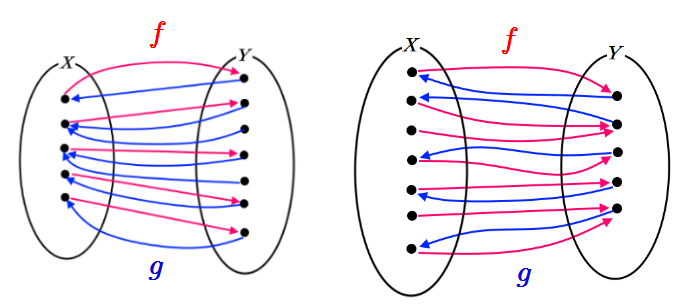
그림2 $g$ left inverse of $f$                                  그림3 $g$ right inverse of $f$

 

예제) 함수 $f~:~\mathbb N \longrightarrow \mathbb N,~f(x)=3x$를 생각해보자. 그러면 함수 $f$는 좌측역함수를 갖음을 보여라.

(증명) $g \circ f \equiv I_{\mathbb N}$를 만족하는 함수 $g$를 찾아보자. 함수 $f$는 $x$를 $3x$에 대응시키므로 함수 $g$를 다음과 같이 정의하자.

$$g(y)=\begin{cases} \frac{y}{3} &(y가 ~3의 ~배수일 ~때)\\1&(y가~3의~배수가~아닐~때)\end{cases}$$

그러면 임의의 $x \in \mathbb N$에 대하여 $(g \circ f)(x)=g(3x)=x$이다. 즉 $g \circ f \equiv I_{\mathbb N}$.

따라서 $g$는 $f$의 좌측역함수이다.                                                                      $\Box$

 

보조정리 5. Let $X,~ Y$ be nonempty sets, and let $f ~: ~X \longrightarrow Y$ be a function. Then

1. $f$ has a left inverse if and only if $f$ is injective.

2. $f$ has a right inverse if and only if $f$ is surjective.

(증명)

1. ($\Rightarrow$) $f$는 좌측역함수 $g$를 갖는다고 가정하자.

이제 $f$가 $1-1$함수임을 보이자.

$x_1 ,~x_2 \in X$에 대하여 $x_1 \neq x_2$이고 $f(x_1 )=f(x_2 )$인 $x_1 ,~x_2$가 존재한다고 가정하자.

$g$가 함수 $f$의 좌측역함수라 하면 $(g \circ f)(x_1 )= x_1 $, $(g \circ f)(x_2 )= x_2$이다. 따라서 $x_1 =x_2$이다.

이것은 $x_1 \neq x_2$라는 가정에 모순이다.

($\Leftarrow$) 함수 $f$가 $1-1$이라 가정하자. 이제 $f$의 좌측역함수 $g$를 다음과 같이 정의하자.

$$g(y)=\begin{cases} x &(f(x)=y)\\ x_0 &(y \neq f(x_0) ,~x_0 \in X)\end{cases}$$

이렇게 정의한 함수 $g$에 대하여 모든 $x \in X$에 대하여

$$(g \circ f)(x)=x$$

따라서 $g$는 $f$의 좌측역함수이다.

2. ($\Rightarrow$) $f$는 우측역함수 $h$를 갖는다고 가정하자.

이제 $f$가 치역과 공역이 같음을 보이자.

귀류법으로 증명하자. $f$가 치역과 공역이 다르다고 가정하자. 그러면 $y_0 \in Y$가 존재하여 모든 $x \in X$에 대하여 $f(x) \neq y_0$ $\cdots\cdots \mathrm{(i)}$

그런데 $y_0 $가 집합 $Y$의 원소이고 함수 $f$가 우측역함수를 가지므로

$$ (f \circ g)(y_0 )=y_0 ~\Longleftrightarrow~f(g(y_0))=y_0 ~(\because ~합성함수의~ 정의) $$

함수 $g$의 공역은 집합 $X$이므로 $g(y_0) \in X$이므로 함수 $f$에 의해 $y_0 $로 가는 $x$가 $x= g(y_0)$로 존재하므로 (i)와 모순이다.

따라서 함수 $f$는 치역과 공역이 같은 함수이다.

 

($\Leftarrow$) 함수 $f$가 치역과 공역이 같은 함수라 하자. $f$가 치역과 공역이 같은 함수이므로 함수 $f$의 공역인 집합 $Y$의 모든 원소에 대응되는 집합 $X$의 원소가 하나이상 존재한다.

이제 $f$의 우측역함수 $h~:~Y \rightarrow X$를 다음과 같이 정의하자. $y \in Y$에 대하여 $h(y)$를 $f(x)=y$를 만족하는 집합 $X$의 원소 $x$ 중 적어도 하나 존재하는데 그 원소 중 어느 한 원소에 대응시킨다.

그러면 함수 $h$는 함수 $f$의 우측역함수(right-inverse)이다.                                   $\Box$

이것을 이해하기 쉽게 그림으로 설명해 보자.

함수 $f~:~X \longrightarrow Y$를 위의 그림처럼 대응시키면 함수 $f$는 치역과 공역이 같은 함수이다. 이제 함수 $f$의 우측역함수 $h~:~Y \longrightarrow X$를 위의 그림에서처럼 대응시키자. 함수 $f$가 치역과 공역이 같은 함수이므로 집합 $Y$의 원소에 대응되는 집합 $X$의 원소는 적어도 하나 존재한다. 만약 대응하는 집합 $X$의 원소가 하나이면 그 원소를 $h$의 함숫값으로 하고 만약 두개 이상이면 그 중 어느 하나의 원소를 함숫값으로 대응시킨다면 그 대응 $h$는 함수가 된다. 위의 그림처럼 $$h(a)=1,~h(b)=4,~h(c)=2,~h(d)=3$$

그러면 이 함수 $h$가 함수 $f$의 우측역함수(right-inverse)가 된다. 즉 모든 $y \in Y$에 대하여 $$(f \circ g)(y)=y $$이다.

우리는 보조정리 5.를 통해 함수 $f$의 좌-우측 역함수를 구체적으로 구하지 않고서도 좌-우측 역함수가 존재함을 증명할 수 있다. 

예) 함수 $f~:~\mathbb R \longrightarrow \mathbb R ,~f(x)=2x+1$가 좌-우측 역함수를 가짐을 보여라.

(증명) 보조정리5에 의해 함수 $f$가 $1-1$함수임과 치역과 공역이 같은 함수임을 보이면 충분하다.

(1) ($1-1$함수)

$\mathbb R$인 임의의 $x_1,~x_2$에 대하여 $f(x_{1})=f(x_{2})$라 가정하면

$$2x_1 +1=2x_2 +1 ~\Longleftrightarrow ~x_1=x_2 $$

따라서 함수 $f$는 일대일 함수이다.

(2) (치역과 공역이 같은 함수)

$\mathbb R$인 임의의 $y$에 대하여 적당한 $x= \frac{y-1}{x}$가 존재하여

$$f(x)=f \left( \frac{y-1}{2}\right)=2 \frac{y-1}{2}+1=y$$

이다. 따라서 함수 $f$는 치역과 공역이 같은 함수이다.

(1), (2)와 보조정리 5에 의해 함수 $f$는 좌우측 역함수를 갖는다.                $\Box$

 

Theorem 6. Let $X$ and $Y$ be sets, and let $f~ :~ X  \longrightarrow Y$ be a function. Then $ f$ has a two-sided inverse if and only if $f$ is bijective.

(증명) ($\Rightarrow$) 함수 $f$가 양측역함수(two-sided inverse)를 갖는다고 가정하면 보조정리 5.에 의해 함수 $f$는 bijective(1-1함수, 치역과 공역이 같은 함수)이다.

($\Leftarrow$) 함수 $f$는 bijective(1-1함수, 치역과 공역이 같은 함수)라고 가정하면 보조정리 5.에 의해 함수 $f$가 양측역함수(two-sided inverse)를 갖는다.               $\Box$

 

따름 정리7. Let $X,~ Y$ be sets, and let $f~ :~ X  \longrightarrow Y$ be a function. If f has a left inverse $g$ and a right inverse $h$, then $g \equiv h$.

(증명) 함수 $f$가 좌측연속함수 $g$, 우측연속함수 $h$를 갖는다고 가정하자. 그러면

$$\begin{align} g &\equiv g \circ I_Y \\& \equiv g \circ ( f \circ h) ~(\because h ~:~ \mathrm{right ~inverse ~of} ~f) \\&\equiv (g \circ f) \circ h ~(\because ~합성함수의 결합법칙)\\& \equiv I_X \circ h ~(\because g~:~\mathrm{left ~inverse~of}~f) \\& \equiv h\end{align}$$

$\Box$

 

예제 함수 $f~:~\mathbb R \longrightarrow \mathbb R,~f(x)=(x-2)^3 $는 역함수를 가짐을 보여라.

우리는 두가지 방법으로 보이자.

(증명1) $g~:~\mathbb R \longrightarrow \mathbb R,~g(x)=\root {3} \of  {x} +2   $로 정의하면

$$(g \circ f)(x)=g((x-2)^3)= x-2+2=x $$ 즉 $g \circ f =I_{\mathbb R}$

$$(f \circ g)(x)=f( \root {3} \of {x}+2) =( \root {3} \of {x} +2-2)^3) = x$$ 즉 $f \circ g =I_{\mathbb R}$.

$g$는 $f$의 역함수이다.

(증명2) 함수 $f$가 bijective($1-1$함수, 치역과 공역이 같은 함수)임을 보이면 충분하다.

 ($1-1$함수) $x_1 ,~x_2 \in \mathbb R$에 대하여 $f(x_1) = f(x_2)$라 가정하자.

$$(x_1 -2)^3 =(x_2 -2)^3 ~\Longleftrightarrow x_1 -2 =x_2 -2 ~\Longleftrightarrow x_1 =x_2 $$

따라서 함수 $f$는 일대일 함수이다.

(치역과 공역이 같은 함수)

임의의 $y \in \mathbb R $에 대하여 $x= \root 3 \of {y} +2$가 존재하여 $$ f(x)=f ( \root {3} \of {y} +2 ) =(\root {3} \of {y} +2-2)^3 =y$$
임으로 함수 $f$는 치역과 공역이 같은 함수이다.

따라서 함수 $f$는 일대일함수이고 치역과 공역이 같은 함수이므로 역함수를 갖는다.  $\Box$

 

https://plusthemath.tistory.com/270

[수학의 기초] 함수의 정의와 함수의 종류 -1

https://plusthemath.tistory.com/272

[수학의 기초] 함수의 정의와 함수의 종류 -2